Prueba de Kolmogorov-Smirnov

La prueba K-S es una prueba de bondad de ajuste utilizada para evaluar la uniformidad de un conjunto de distribuciones de datos. Se diseñó en respuesta a las deficiencias de la prueba de chi-cuadrado, que produce resultados precisos sólo para distribuciones discretas y binadas. La prueba K-S tiene la ventaja de no hacer ninguna suposición sobre la división en lotes de los conjuntos de datos que se van a comparar, eliminando la naturaleza arbitraria y la pérdida de información que acompaña al proceso de selección de lotes.

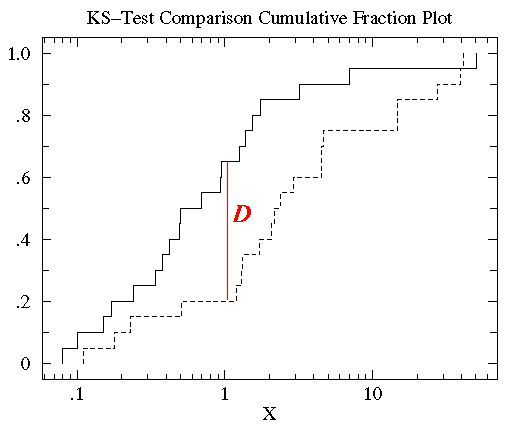
En estadística, la prueba K-S es la prueba aceptada para medir las diferencias entre los conjuntos de datos continuos (distribuciones de datos sin agrupar) que son una función de una sola variable. Esta medida de diferencia, el estadístico K-S \(D\), se define como el valor máximo de la diferencia absoluta entre dos funciones de distribución acumulativa. La prueba K-S unilateral se utiliza para comparar un conjunto de datos con una función de distribución acumulativa conocida, mientras que la prueba K-S bilateral compara dos conjuntos de datos diferentes. Cada conjunto de datos da una función de distribución acumulativa diferente, y su importancia reside en su relación con la distribución de probabilidad de la que se extrae el conjunto de datos: la función de distribución de probabilidad para una única variable independiente \(x\) es una función que asigna una probabilidad a cada valor de \(x\). La probabilidad asumida por el valor específico \(x_{i}\) es el valor de la función de distribución de probabilidad en \(x_{i}\) y se denota \(P(x_{i})\N.)La función de distribución acumulativa se define como la función que da la fracción de los puntos de datos a la izquierda de un valor dado \(x_{i}), \(P(x <x_{i})\Nrepresenta la probabilidad de que \N(x\N) sea menor o igual que un valor específico \N(x_{i}).

Así, para comparar dos funciones de distribución acumulativa diferentes \(S_{N1}(x)\) y \(S_{N2}(x)\), el estadístico K-S es

D = max|S_N1(x) – S_N2(x)|

donde \(S_{N}(x)\) es la función de distribución acumulativa de la distribución de probabilidad de la que se extrae un conjunto de datos con \(N\) eventos. Si \(N\) eventos ordenados se encuentran en los puntos de datos \(x_{i}\), donde \(i = 1, \ldots, N\), entonces

S_N(x_i) = (i-N)/N

donde la matriz de datos \(x\) se ordena en orden creciente. Esta es una función escalonada que se incrementa en \(1/N\) en el valor de cada punto de datos ordenado.

Para nuestros fines, las dos distribuciones comparadas son la distribución medida de los tiempos de llegada, y la fracción acumulada en el intervalo de tiempo transcurrido. Si se cumple la hipótesis nula (sin variabilidad), obtenemos el 50% de sus eventos en el 50% del tiempo transcurrido, y el estadístico \(D\) debería distribuirse según la distribución de Kolmogorov para muchas realizaciones de la distribución de tiempos de llegada. La probabilidad devuelta por la prueba es, pues, \(p_{KS} = 1 – \alpha\), donde \(\alpha\) es la probabilidad (bajo la distribución de Kolmogorov) de que el valor de \(D\) sea mayor o igual que el valor medido. Por lo tanto, un valor pequeño de \(p_{KS}\a) indica consistencia con la hipótesis nula, mientras que un valor grande de \(p_{KS}\a) indica que el intervalo entre eventos no es constante, y por lo tanto se puede inferir la variabilidad.