Christian Bohr e o conceito de ligação cooperativaEditar
Em 1904, Christian Bohr estudou a ligação da hemoglobina ao oxigénio sob diferentes condições. Ao traçar a saturação da hemoglobina com oxigênio em função da pressão parcial de oxigênio, ele obteve uma curva sigmoidal (ou “em forma de S”). Isso indica que quanto mais oxigênio estiver ligado à hemoglobina, mais fácil será a ligação de mais oxigênio – até que todos os locais de ligação estejam saturados. Além disso, Bohr notou que o aumento da pressão de CO2 deslocou essa curva para a direita – ou seja, maiores concentrações de CO2 tornam mais difícil para a hemoglobina se ligar ao oxigênio. Este último fenômeno, juntamente com a observação de que a afinidade da hemoglobina pelo oxigênio aumenta com o aumento do pH, é conhecido como efeito Bohr.

Diz-se que uma molécula receptora exibe ligação cooperativa se a sua ligação a escalas ligand não lineares com concentração ligand. A cooperatividade pode ser positiva (se a ligação de uma molécula de ligando aumenta a afinidade aparente do receptor e, portanto, aumenta a chance de ligação de outra molécula de ligando) ou negativa (se a ligação de uma molécula de ligando diminui a afinidade e, portanto, torna menos provável a ligação de outras moléculas de ligando). A “ocupação fracionária” Y ¯ ¯bar ¯ estilo de jogo ¯

de um receptor com um determinado ligando é definido como a quantidade de sítios de ligação ligando dividido pela quantidade total de sítios de ligação ligando: Y ¯ = + = {\frac {\bar {\bar {\bar }}={\frac {\frac {\frac {}}={\frac}
If Y ¯ = 0 {\i}displaystyle {\i}bar {\i}=0}
>

, então a proteína está completamente sem restrições, e se Y ¯ = 1 {\a {\a {\a }=1}

, está completamente saturado. Se a trama de “Y” for ao estilo de “Y”, “Bar”…

em equilíbrio em função da concentração ligante é sigmoidal, como observado por Bohr para a hemoglobina, isto indica uma cooperatividade positiva. Se não for, nenhuma afirmação pode ser feita sobre a cooperatividade apenas olhando para este gráfico.
O conceito de ligação cooperativa só se aplica a moléculas ou complexos com mais de um local de ligação ligando. Se existirem vários locais de ligação de ligantes, mas a ligação de ligantes a qualquer local não afecta os outros, diz-se que o receptor é não-cooperativo. A cooperatividade pode ser homotrópica, se um ligando influenciar a ligação de ligandos do mesmo tipo, ou heterotrópica, se influenciar a ligação de outros tipos de ligandos. No caso da hemoglobina, Bohr observou uma cooperatividade homotrópica positiva (a ligação do oxigênio facilita a ligação de mais oxigênio) e heterotrópica negativa (a ligação do CO2 reduz a facilidade da hemoglobina em ligar o oxigênio.)
Ao longo do século XX, várias estruturas foram desenvolvidas para descrever a ligação de um ligante a uma proteína com mais de um local de ligação e os efeitos cooperativos observados neste contexto.
A equação HillEdit
A primeira descrição de ligação cooperativa a uma proteína de múltiplos locais foi desenvolvida por A.V. Hill. Com base nas observações da ligação do oxigênio à hemoglobina e na idéia de que a cooperatividade surgiu da agregação de moléculas de hemoglobina, cada uma ligando uma molécula de oxigênio, Hill sugeriu uma equação fenomenológica que desde então recebeu o seu nome:
Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\\displaystyle {\bar {\\\\d}}={\frac {\d} ^{\n}}{1+K\cdot ^{\n}}={\frac {\n}{K^{*}+^{\n}}={\frac {\d}{K_{\d}^{n}+^{n}}}}

é o “coeficiente de colina”, {\\i1}estilo de exibição {\i}

denota concentração de ligando, K ^{\displaystyle K}

denota uma constante de associação aparente (usada na forma original da equação), K ∗ ^{\displaystyle K^{*}}

é uma constante de dissociação empírica, e K d {\i1}displaystyle K_{d}}

uma constante de dissociação microscópica (usada nas formas modernas da equação, e equivalente a um E C 50 {\an8}mathrm {\an8} _{50}}

). Se n < 1 {\\displaystyle n<1}}{\displaystyle n<1}

, o sistema exibe uma cooperatividade negativa, enquanto que a cooperatividade é positiva se n > 1 {\\i1}displaystyle n>1}

. O número total de locais de ligação ligando é um limite superior para n {\i1}displaystyle n

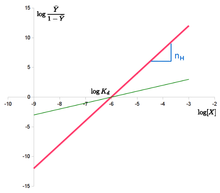
. A equação Hill pode ser linearizada como: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\i1}log {\i1}{\i1}frac {\i}{\i1-{\i1}bar {\i}}}}=n=n-cdot {\i}log-n-cdot {\i}log K_{\i}

. No caso da equação Hill, é uma linha com a inclinação n H {\i1}displaystyle n_{H}}

e log de intercepção ( K d ) {\i1}displaystyle {\i}log(K_{d})}

. Isto significa que se assume que a cooperatividade é fixa, ou seja, não muda com a saturação. Isso também significa que os locais de ligação sempre exibem a mesma afinidade, e a cooperatividade não surge de uma afinidade crescente com a concentração de ligantes.
A equação de AdairEdit
G.S. Adair descobriu que o gráfico de Hill para hemoglobina não era uma linha reta, e levantou a hipótese de que a afinidade de ligação não era um termo fixo, mas dependente da saturação ligand. Tendo demonstrado que a hemoglobina continha quatro hemes (e, portanto, locais de ligação para o oxigênio), ele trabalhou a partir da suposição de que a hemoglobina totalmente saturada é formada em estágios, com formas intermediárias com uma, duas ou três moléculas de oxigênio ligadas. A formação de cada estágio intermediário a partir da hemoglobina não ligada pode ser descrita usando uma aparente constante de associação macroscópica K i {\i}}.

. A ocupação fracionária resultante pode ser expressa como: Y ¯ = 1 4 ⋅ K I + 2 K I I I 2 + 3 K I I I 3 + 4 K I V 4 1 + K I I + K I I 2 + K I I I I 3 + K I V 4 {\i}displaystyle {\i}bar Frac… {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, para qualquer proteína com locais de ligação n ligand:
Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … K n n n {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}+2K_{\i}+2K_{\i}^{\i}+ pontos +nK_{\i}^{\i}{1+K_{\i}+K_{\i}{\i}+ pontos +K_{\i}^{\i}}}}

onde n denota o número de sites vinculados e cada K i {\i}}

é uma constante de associação combinada, descrevendo a ligação das moléculas de i ligand. Ao combinar o tratamento Adair com a trama Hill, chega-se à definição experimental moderna de cooperatividade (Hill, 1985, Abeliovich, 2005). O coeficiente de Hill resultante, ou mais corretamente a inclinação da parcela de Hill calculada a partir da Equação de Adair, pode ser mostrado como a razão entre a variância do número de ligação e a variância do número de ligação em um sistema equivalente de locais de ligação não-interactivos. Assim, o coeficiente de Hill define a cooperatividade como uma dependência estatística de um local de ligação em relação ao estado de outro(s) local(is).
A equação de KlotzEdit
Trabalho com proteínas de ligação do cálcio, Irving Klotz deconvolucionou as constantes de associação de Adair considerando a formação gradual dos estágios intermediários, e tentou expressar a ligação cooperativa em termos de processos elementares governados pela lei de ação de massa. Na sua estrutura, K 1 {\i1}displaystyle K_{\i}

é a constante de associação que rege a ligação da primeira molécula de ligando, K 2 {\\\i1}

a constante de associação que rege a ligação da segunda molécula de ligante (uma vez que a primeira já está ligada), etc. Para Y ¯ ¯ barra ¯x

, isto dá: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … + … K n ) n estilo de jogo {\i1}{\i1}{\i1}{\i1}{\i1}K_{\i}+2K_{\i}K_{\i}^{\i1}+ pontos +n-esquerda(K_{\i}K_{\i}{\i}}}ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Vale a pena notar que as constantes K 1 {{\i1}displaystyle K_{\i}

, K 2 {\i1}displaystyle K_{2}}

e assim por diante não se relacionam com sites de ligação individual. Eles descrevem quantos locais de ligação estão ocupados, em vez de quais. Esta forma tem a vantagem de que a cooperatividade é facilmente reconhecida quando se consideram as constantes da associação. Se todos os locais de ligação de ligantes são idênticos a uma constante de associação microscópica K {\displaystyle K}

, seria de esperar K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\\i1}=nK,K_{\i}={\i1}{\i1}K,{\i}ldots K_{\i}={\i1}K}

(isto é K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}K}

) na ausência de cooperação. Temos uma cooperatividade positiva se K i {\i}}{\i} K_{\i}

está acima destes valores esperados para i > 1 {\displaystyle i>1}

.
A equação de Klotz (que às vezes também é chamada de equação de Adair-Klotz) ainda é freqüentemente usada na literatura experimental para descrever medidas de ligand binding em termos de constantes seqüenciais de binding aparente.
Equação de PaulingEdit
Em meados do século XX, havia um interesse crescente em modelos que não apenas descrevessem fenomenologicamente curvas de binding, mas oferecessem um mecanismo bioquímico subjacente. Linus Pauling reinterpretou a equação fornecida por Adair, assumindo que suas constantes eram a combinação da constante de ligação para o ligando ( K {\displaystyle K}

na equação abaixo) e energia proveniente da interação entre subunidades da proteína cooperativa ( α {\displaystyle \alpha }

abaixo). Pauling realmente derivou várias equações, dependendo do grau de interação entre as subunidades. Baseado em suposições erradas sobre a localização de hemes, ele optou pela errada para descrever a ligação de oxigênio pela hemoglobina, assumindo que as subunidades foram dispostas em um quadrado. A equação abaixo fornece a equação para uma estrutura tetraédrica, que seria mais precisa no caso da hemoglobina: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 3 + α 6 K 4 4 4 {\i1}bar {\i}={\i1}frac {\i}K+3}alpha K^{}K^{2}^{2}+3}alfa {}^{3}K^{3}^{3}+}alfa {}^{6}K^{4}^{4}}{1+4K+6}alfa {}K^{2}^{2}+4}alfa {}^{3}K^{3}+^{3}+}alfa {}^{6}K^{4}^{4}}}}

O modelo KNFEdit
Baseado em resultados que mostram que a estrutura das proteínas cooperativas mudou após a ligação ao seu ligante, Daniel Koshland e colegas refinaram a explicação bioquímica do mecanismo descrito por Pauling. O modelo Koshland-Némethy-Filmer (KNF) assume que cada subunidade pode existir em uma de duas conformações: ativa ou inativa. A ligação de Ligand a uma subunidade induziria uma mudança conformacional imediata dessa subunidade da inativa para a ativa, um mecanismo descrito como “ajuste induzido”. A cooperatividade, de acordo com o modelo KNF, surgiria das interações entre as subunidades, cuja força varia dependendo das conformações relativas das subunidades envolvidas. Para uma estrutura tetraédrica (também consideradas estruturas lineares e quadradas), eles propuseram a seguinte fórmula:
Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\displaystyle {\displaystyle {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Onde K X {\\i1}displaystyle K_{\i}}

é a constante de associação para X, K t {\t}}

é a razão entre os estados B e A na ausência de ligando (“transição”), K A B {\i1}displaystyle K_{AB}}

e K B B B {\\a10}}displaystyle K_{BB}}

são as estabilidades relativas dos pares de subunidades vizinhas em relação a um par onde ambas as subunidades estão no estado A (Note que o papel da KNF apresenta N s {\i1}{\i1}

, o número de locais ocupados, que está aqui 4 vezes Y ¯bar {\an8}}

).
O modelo MWCEditar


>
O modelo Monod-Wyman-Changeux (MWC) para transições alostéricas concertadas foi um passo à frente ao explorar a cooperatividade baseada na termodinâmica e conformações tridimensionais. Foi originalmente formulado para proteínas oligoméricas com subunidades idênticas e dispostas simetricamente, cada uma das quais com um local de ligação ligante. De acordo com esta estrutura, dois (ou mais) estados conformacionais interconversíveis de uma proteína alostérica coexistem em equilíbrio térmico. Os estados – frequentemente denominados de tenso (T) e relaxado (R) – diferem em afinidade para a molécula ligante. A relação entre os dois estados é regulada pela ligação das moléculas ligantes que estabiliza o estado de maior afinidade. Importante, todas as subunidades de uma molécula mudam de estado ao mesmo tempo, um fenómeno conhecido como “transição concertada”.
A constante de isomerização alostérica L descreve o equilíbrio entre ambos os estados quando nenhuma molécula ligando é ligada: L = {\\i1}esquerda L={\i}{\i}{\i1}esquerda

. Se L for muito grande, a maior parte da proteína existe no estado T na ausência de ligando. Se L é pequeno (perto de um), o estado R é quase tão povoado como o estado T. A razão das constantes de dissociação para o ligando dos estados T e R é descrita pela constante c: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Se c = 1 {\displaystyle c=1}{\displaystyle c=1}

, ambos os estados R e T têm a mesma afinidade para o ligando e o ligando não afecta a isomerização. O valor de c também indica quanto o equilíbrio entre os estados T e R muda na ligação ligando: quanto menor o c, mais o equilíbrio se desloca para o estado R após uma ligação. Com α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}
 , a ocupação fracionária é descrita como: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\i1}{\i1}={\i1}frac ^{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i1}n1}+Lc\alpha (1+c\alpha )^{n-1}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}
, a ocupação fracionária é descrita como: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\i1}{\i1}={\i1}frac ^{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i}{\i1}n1}+Lc\alpha (1+c\alpha )^{n-1}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

A parcela sigmóide Hill das proteínas alostéricas pode então ser analisada como uma transição progressiva do estado T (baixa afinidade) para o estado R (alta afinidade) à medida que a saturação aumenta. A inclinação da parcela de Hill também depende da saturação, com um valor máximo no ponto de inflexão. As interceptações entre as duas assímptotas e o eixo y permitem determinar as afinidades de ambos os estados para o ligante.

Em proteínas, a mudança conformacional é frequentemente associada à atividade, ou atividade em direção a alvos específicos. Tal atividade é muitas vezes o que é fisiologicamente relevante ou o que é medido experimentalmente. O grau de mudança conformacional é descrito pela função de estado R ¯ {\i} {\i} {\i1}

, que denota a fração de proteína presente no R {\i1}displaystyle R

state. Como o diagrama de energia ilustra, R ¯ ¯ barra de exibição {\i}}

aumenta à medida que mais moléculas de ligante se ligam. A expressão para R ¯ ¯ ¯bar ¯bar ¯

é: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n ^{\i1}{\i1}={\i1 + α ) n ^{\i}={\i1}frac ^{(1+\i}alfa )^{\i}{(1+\i}alfa )^{\i}+L(1+c\i}alfa )^{n}}}}

Um aspecto crucial do modelo MWC é que as curvas ao estilo Y ¯ ¯bar {\i}{\i}

e R ¯displaystyle {\i}{\i}

não coincidem, ou seja, a saturação fracionária não é um indicador direto do estado conformacional (e, portanto, da atividade). Além disso, as extensões da cooperatividade de ligação e da cooperatividade de activação podem ser muito diferentes: um caso extremo é fornecido pelo motor da bactéria flagella com um coeficiente de Hill de 1,7 para a ligação e de 10,3 para a activação. A supra linearidade da resposta é por vezes chamada ultra-sensibilidade.
Se uma proteína alostérica se liga a um alvo que também tem uma maior afinidade com o estado R, então a ligação ao alvo estabiliza ainda mais o estado R, aumentando assim a afinidade ligand. Se, por outro lado, um alvo se liga preferencialmente ao estado T, então a ligação do alvo terá um efeito negativo sobre a afinidade ligandar. Tais alvos são chamados de moduladores alostéricos.
Desde o seu início, a estrutura MWC tem sido estendida e generalizada. Variações foram propostas, por exemplo, para atender a proteínas com mais de dois estados, proteínas que se ligam a vários tipos de ligantes ou vários tipos de moduladores alostéricos e proteínas com subunidades não idênticas ou locais de ligação de ligantes.