El flujo de StatsTest: Predicción >> Variable Dependiente Continua >> Más de una Variable Independiente >> Sin Medidas Repetidas >> Una Variable Dependiente
¿No está seguro de que este es el método estadístico correcto? Utilice el flujo de trabajo Elija su prueba estadística para seleccionar el método correcto.
- ¿Qué es la regresión lineal múltiple multivariada?
- Supuestos para la Regresión Lineal Múltiple Multivariante
- Linealidad
- Sin valores atípicos
- Distribución similar a través del rango
- Normalidad de los residuos
- Sin multicolinealidad
- ¿Cuándo utilizar la regresión lineal múltiple multivariante?
- Predicción
- Variable dependiente continua
- Más de una variable independiente
- Ejemplo de regresión lineal múltiple multivariada
- Preguntas frecuentes
- ¡Ayuda!
¿Qué es la regresión lineal múltiple multivariada?
La regresión lineal múltiple multivariada es una prueba estadística utilizada para predecir múltiples variables de resultado utilizando una o más variables. También se utiliza para determinar la relación numérica entre estos conjuntos de variables y otros. La variable que desea predecir debe ser continua y sus datos deben cumplir los demás supuestos que se indican a continuación.
Supuestos para la Regresión Lineal Múltiple Multivariante
Todo método estadístico tiene supuestos. Los supuestos significan que sus datos deben satisfacer ciertas propiedades para que los resultados del método estadístico sean precisos.
Los supuestos para la Regresión Lineal Múltiple Multivariante incluyen:
- Linealidad
- Sin valores atípicos
- Distribución similar a lo largo del rango
- Normalidad de los residuos
- Sin multicolinealidad
Vamos a profundizar en cada uno de ellos por separado.
Linealidad
Las variables que le interesan deben estar relacionadas linealmente. Esto significa que si traza las variables, podrá dibujar una línea recta que se ajuste a la forma de los datos.
Sin valores atípicos
Las variables que le interesan no deben contener valores atípicos. La regresión lineal es sensible a los valores atípicos, o puntos de datos que tienen valores inusualmente grandes o pequeños. Puede saber si sus variables tienen valores atípicos graficándolos y observando si algún punto está lejos de todos los demás puntos.
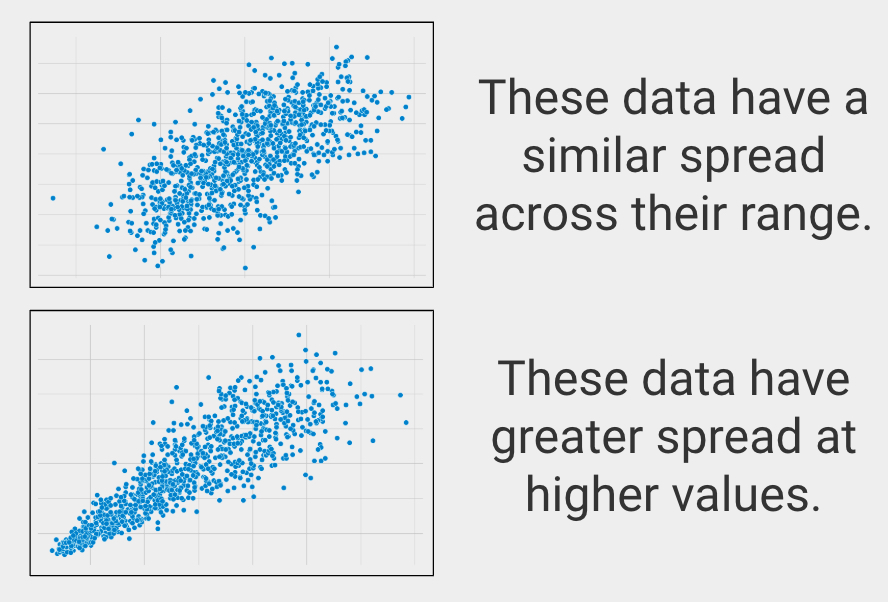
Distribución similar a través del rango
En estadística esto se llama homocedasticidad, que describe cuando las variables tienen una distribución similar a través de sus rangos.
Normalidad de los residuos
La palabra “residuos” se refiere a los valores resultantes de restar las variables dependientes esperadas (o predichas) de los valores reales. La distribución de estos valores debe ajustarse a una forma de distribución normal (o curva de campana).
El cumplimiento de este supuesto asegura que los resultados de la regresión son igualmente aplicables en toda la extensión de los datos y que no hay un sesgo sistemático en la predicción.
Sin multicolinealidad
La multicolinealidad se refiere al escenario en el que dos o más de las variables independientes están sustancialmente correlacionadas entre sí. Cuando la multicolinealidad está presente, los coeficientes de regresión y la significación estadística se vuelven inestables y menos fiables, aunque no afecta a lo bien que el modelo se ajusta a los datos per se.
¿Cuándo utilizar la regresión lineal múltiple multivariante?
Debería utilizar la regresión lineal múltiple multivariante en el siguiente escenario:
- Desea utilizar una variable en una predicción de otras múltiples variables, o desea cuantificar la relación numérica entre ellas
- Las variables que desea predecir (su variable dependiente) son continuas
- Tiene más de una variable independiente, o una variable que está utilizando como predictor
- No tiene medidas repetidas de la misma unidad de observación
- Tiene más de una variable dependiente
Aclaremos esto para ayudarle a saber cuándo utilizar la regresión lineal múltiple multivariante.
Predicción
Está buscando una prueba estadística para predecir una variable utilizando otra. Esta es una pregunta de predicción. Otros tipos de análisis incluyen el examen de la fuerza de la relación entre dos variables (correlación) o el examen de las diferencias entre grupos (diferencia).
Variable dependiente continua
La variable que desea predecir debe ser continua. Continua significa que su variable de interés puede tomar básicamente cualquier valor, como la frecuencia cardíaca, la altura, el peso, el número de barras de helado que puede comer en 1 minuto, etc.
Los tipos de datos que NO son continuos incluyen datos ordenados (como el lugar de llegada en una carrera, los mejores rankings de negocios, etc.), datos categóricos (género, color de ojos, raza, etc.), o datos binarios (compró el producto o no, tiene la enfermedad o no, etc.).
Si su variable dependiente es binaria, debe utilizar la Regresión Logística Múltiple, y si su variable dependiente es categórica, entonces debe utilizar la Regresión Logística Multinomial o el Análisis Discriminante Lineal.
Más de una variable independiente
La regresión lineal múltiple se utiliza cuando hay una o más variables predictoras con múltiples valores para cada unidad de observación.
Sin medidas repetidas
Este método es adecuado para el escenario cuando sólo hay una observación para cada unidad de observación. La unidad de observación es lo que compone un “punto de datos”, por ejemplo, una tienda, un cliente, una ciudad, etc…
Si tiene una o más variables independientes pero se miden para el mismo grupo en múltiples puntos del tiempo, entonces debe utilizar un Modelo de Efectos Mixtos.
Más de una variable dependiente
Para ejecutar la regresión lineal múltiple multivariada, debe tener más de una variable dependiente, o variable que está tratando de predecir.
Si sólo está prediciendo una variable, debe utilizar la regresión lineal múltiple.
Ejemplo de regresión lineal múltiple multivariada
Variable dependiente 1: Ingresos
Variable dependiente 2: Tráfico de clientes
Variable independiente 1: Dólares gastados en publicidad por ciudad
Variable independiente 2: Población de la ciudad
La hipótesis nula, que es la jerga estadística para lo que sucedería si el tratamiento no hace nada, es que no hay relación entre el gasto en publicidad y los dólares de publicidad o la población por ciudad. Nuestra prueba evaluará la probabilidad de que esta hipótesis sea cierta.
Reunimos nuestros datos y, tras asegurarnos de que se cumplen los supuestos de la regresión lineal, realizamos el análisis.
Este análisis ejecuta efectivamente la regresión lineal múltiple dos veces utilizando ambas variables dependientes. Así, cuando ejecutamos este análisis, obtenemos coeficientes beta y valores p para cada término en el modelo de “ingresos” y en el modelo de “tráfico de clientes”. Para cualquier modelo de regresión lineal, tendrá un coeficiente beta que es igual al intercepto de su línea de regresión lineal (a menudo etiquetado con un 0 como β0). Esto es simplemente el lugar donde la línea de regresión cruza el eje Y si se trazan los datos. En el caso de la regresión lineal múltiple, hay además otros dos coeficientes beta (β1, β2, etc), que representan la relación entre las variables independientes y dependientes.
Estos coeficientes beta adicionales son la clave para entender la relación numérica entre sus variables. Esencialmente, por cada unidad (valor de 1) de aumento en una determinada variable independiente, se espera que su variable dependiente cambie en el valor del coeficiente beta asociado a esa variable independiente (manteniendo constantes las demás variables independientes).
El valor p asociado a estos valores beta adicionales es la posibilidad de ver nuestros resultados asumiendo que realmente no hay relación entre esa variable y los ingresos. Un valor p menor o igual a 0,05 significa que nuestro resultado es estadísticamente significativo y podemos confiar en que la diferencia no se debe únicamente al azar. Para obtener un valor p global para el modelo y valores p individuales que representen los efectos de las variables en los dos modelos, se suelen utilizar MANOVAs.
Además, este análisis dará como resultado un valor R-Cuadrado (R2). Este valor puede oscilar entre 0 y 1 y representa lo bien que la línea de regresión lineal se ajusta a los puntos de datos. Cuanto más alto sea el R2, mejor se ajustará su modelo a los datos.
Preguntas frecuentes
P: ¿Cuál es la diferencia entre la regresión lineal múltiple multivariante y la ejecución de la regresión lineal múltiple?
A: Son conceptualmente similares, ya que los coeficientes individuales del modelo serán los mismos en ambos escenarios. Una diferencia sustancial, sin embargo, es que las pruebas de significación y los intervalos de confianza para la regresión lineal multivariante tienen en cuenta las múltiples variables dependientes.
P: ¿Cómo ejecuto la regresión lineal múltiple multivariante en SPSS, R, SAS o STATA?
A: Este recurso se centra en ayudarle a elegir el método estadístico correcto en todo momento. Hay muchos recursos disponibles para ayudarle a averiguar cómo ejecutar este método con sus datos:
Artículo de R: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/
¡Ayuda!
Si todavía no puede averiguar algo, no dude en ponerse en contacto con nosotros.