Grafer i Python

Grafteorins ursprung

Innan vi börjar med de faktiska implementeringarna av grafer i Python och innan vi börjar med introduktionen av Pythonmoduler som behandlar grafer, vill vi ägna oss åt grafteorins ursprung.
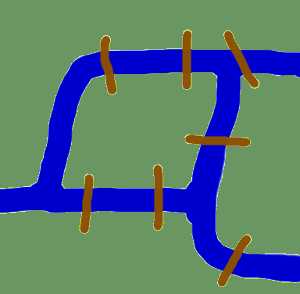
Ursprunget tar oss tillbaka i tiden till Künigsberg på 1700-talet. Königsberg var en stad i Preussen på den tiden. Floden Pregel flöt genom staden och skapade två öar. Staden och öarna var förbundna med sju broar enligt bilden. Invånarna i staden berördes av frågan om det var möjligt att göra en promenad genom staden genom att besöka varje område i staden och korsa varje bro endast en gång? Varje bro måste ha korsats helt och hållet, dvs. det är inte tillåtet att gå halvvägs in på en bro och sedan vända om och senare korsa den andra halvan från andra sidan. Promenaden behöver inte börja och sluta på samma plats. 1735 löste Leonhard Euler problemet genom att bevisa att det inte är möjligt. Han kom fram till att valet av rutt inom varje landområde är irrelevant och att det enda som spelar roll är i vilken ordning (eller sekvens) broarna korsas. Han hade formulerat en abstraktion av problemet genom att eliminera onödiga fakta och fokusera på landområdena och broarna som förbinder dem. På så sätt skapade han grunderna för grafteorin. Om vi ser ett “landområde” som ett hörn och varje bro som en kant har vi “reducerat” problemet till en graf.

Introduktion till grafteori med hjälp av Python

Innan vi börjar vår behandling av möjliga Python-representationer av grafer vill vi presentera några allmänna definitioner av grafer och dess beståndsdelar.
En “graf “1 inom matematik och datavetenskap består av “noder”, även kallade “hörn”, och noder kan vara anslutna till varandra eller inte. I vår illustration – som är en bildlig representation av en graf – är noden “a” kopplad till noden “c”, men “a” är inte kopplad till “b”. Den linje som förbinder två noder kallas för en kant. Om kanterna mellan noderna är oledda kallas grafen för en oledd graf. Om en kant är riktad från en topp (nod) till en annan kallas grafen för en riktad graf. En riktad kant kallas för en båge.
Tyvärr kan grafer se väldigt teoretiska ut, men många praktiska problem kan representeras av grafer. De används ofta för att modellera problem eller situationer inom fysik, biologi, psykologi och framför allt inom datavetenskap. Inom datavetenskapen används grafer för att representera kommunikationsnätverk, dataorganisation, beräkningsenheter, beräkningsflödet,

I det senare fallet används graferna för att representera dataorganisationen, som filsystemet i ett operativsystem, eller kommunikationsnätverk. Länkstrukturen på webbplatser kan också ses som en graf, dvs. en riktad graf, eftersom en länk är en riktad kant eller en båge.
Python har ingen inbyggd datatyp eller klass för grafer, men det är lätt att implementera dem i Python. En datatyp är idealisk för att representera grafer i Python, nämligen ordböcker. Grafen i vår illustration kan implementeras på följande sätt:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Nycklarna i ordboken ovan är noderna i vår graf. Motsvarande värden är listor med noderna, som förbinds genom en kant. Det finns inget enklare och elegantare sätt att representera en graf.
En kant kan ses som en 2-tupel med noder som element, dvs. (“a”, “b”)
Funktion för att generera listan över alla kanter:Denna kod genererar följande utdata, om den kombineras med det tidigare definierade graflexikonet:

 $ python3 graph_simple.py 

Som vi kan se finns det ingen kant som innehåller noden “f”. “f” är en isolerad nod i vår graf.
Följande Python-funktion beräknar de isolerade noderna i en given graf:Om vi anropar denna funktion med vår graf kommer en lista som innehåller “f” att returneras:

Grafer som Python-klass

Innan vi fortsätter med att skriva funktioner för grafer har vi ett första försök med en implementering av en grafklass i Python. Om du tittar på följande listning av vår klass kan du se i __init__-metoden att vi använder ett lexikon “self.__graph_dict” för att lagra vertices och deras motsvarande intilliggande vertices.
Om du startar den här modulen fristående får du följande resultat:

Stigar i grafer

Vi vill nu hitta den kortaste vägen från en nod till en annan nod. Innan vi kommer till Pythonkoden för detta problem måste vi presentera några formella definitioner.
Närliggande hörn:
Två hörn är näraliggande när de båda är intill en gemensam kant.
Stig i en odirigerad graf:
En stig i en odirigerad graf är en sekvens av hörn P = ( v1, v2, …., vn ) ∈ V x V x … x V så att vi gränsar till v{i+1} för 1 ≤ i < n. En sådan sökväg P kallas för en sökväg av längd n från v1 till vn.
En enkel sökväg:
En sökväg utan upprepade hörn kallas för en enkel sökväg.
Exempel:
(a, c, e) är en enkel sökväg i vår graf, liksom (a,c,e,b). (a,c,e,b,c,d) är en bana men inte en enkel bana, eftersom noden c förekommer två gånger.
Följande metod hittar en bana från en startvertikal till en slutvertikal:Om vi sparar vår grafklass inklusive find_path-metoden som “graphs.py” kan vi kontrollera hur vår find_path-funktion fungerar:Resultatet av föregående program ser ut så här:

Metoden find_all_paths hittar alla vägar mellan en startvertex och en slutvertex:Vi ändrade vår exempelgraf något genom att lägga till kanter från “a” till “f” och från “f” till “d” för att testa den tidigare definierade metoden:Resultatet ser ut så här:

Grad

Grad för en topp v i en graf är antalet kanter som förbinder den, där slingor räknas två gånger. Graden för en vertex v betecknas deg(v). Den maximala graden i en graf G, betecknad med Δ(G), och den minimala graden i en graf, betecknad med δ(G), är den maximala och minimala graden för dess hörn.
I grafen till höger är den maximala graden 5 vid vertex c och den minimala graden 0, dvs. den isolerade vertexen f.
Om alla grader i en graf är lika stora är grafen en regelbunden graf.I en regelbunden graf är alla grader lika stora, och därför kan vi tala om gradens grad.
Gradssummaformeln (Handshaking lemma):
∑v &in; Vdeg(v) = 2 |E|
Detta innebär att summan av graderna för alla hörn är lika med antalet kanter multiplicerat med 2. Vi kan dra slutsatsen att antalet hörn med udda grader måste vara jämnt. Detta påstående är känt som handshaking-lemmat. Namnet “handshaking lemma” härstammar från ett populärt matematiskt problem: I en grupp människor är antalet människor som har skakat hand med ett udda antal andra människor i gruppen jämnt.
Med följande metod beräknas graden av en topp:
Med följande metod beräknas en lista som innehåller de isolerade topparna i en graf:Metoderna delta och Delta kan användas för att beräkna den lägsta respektive högsta graden av en topp:

Gradsekvens

Gradsekvensen för en odirigerad graf definieras som sekvensen av dess toppgrader i icke ökande ordning.
Följande metod returnerar en tupel med gradsekvensen för instansgrafen:
Gradsekvensen för vår exempelgraf är följande sekvens av heltal: (5,2,1,1,1,0).
Isomorfiska grafer har samma gradsekvens. Två grafer med samma gradsekvens är dock inte nödvändigtvis isomorfa.
Det finns en fråga om en given gradsekvens kan realiseras av en enkel graf. Erdös-Gallai-satsen säger att en icke ökande sekvens av n tal di (fori = 1, …, n) är gradsekvensen för en enkel graf om och endast om summan av sekvensen är jämn och följande villkor är uppfyllt:

Uppsättning av Erdös-Gallai-satsen

Vår grafklass – se längre ner för en fullständig lista – innehåller en metod “erdoes_gallai” som avgör om en sekvens uppfyller Erdös-Gallai-satsen. Först kontrollerar vi om summan av elementen i sekvensen är udda. Om så är fallet returnerar funktionen False, eftersom Erdös-Gallai-satsen inte längre kan uppfyllas. Därefter kontrollerar vi med den statiska metoden is_degree_sequence om den inmatade sekvensen är en gradsekvens, dvs. att elementen i sekvensen är icke ökande. Detta är ganska överflödigt, eftersom det är meningen att inmatningen ska vara en gradsekvens, så du kan släppa denna kontroll av effektivitetsskäl. Nu kontrollerar vi i det andra if-uttalandet om teoremets okvation är uppfylld:

Version utan testet för överflödig gradsekvens:

Grafttäthet

Grafttätheten definieras som förhållandet mellan antalet kanter i en given graf och det totala antalet kanter som grafen skulle kunna ha. Med andra ord: Den mäter hur nära en given graf är en komplett graf.
Den maximala tätheten är 1, om en graf är komplett. Detta är tydligt eftersom det maximala antalet kanter i en graf beror på hörnen och kan beräknas som:
max. antal kanter = ½ * |V| * ( |V| – 1 ).
Å andra sidan är den minimala tätheten 0, om grafen inte har några kanter, dvs. det är en isolerad graf.
För oriktade enkla grafer definieras graftätheten som: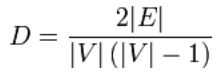

En tät graf är en graf där antalet kanter ligger nära det maximala antalet kanter. En graf med endast ett fåtal kanter kallas en gles graf. Definitionen för dessa två termer är inte särskilt skarp, dvs. det finns ingen minsta övre gräns (supremum) för en sparsam täthet och ingen största nedre gräns (infimum) för att definiera en tät graf.
Den mest precisa matematiska notationen använder den stora O-notationen:
Sparse Graph:
Täta grafer:
En tät graf är en graf G = (V, E) där |E| = Θ(|V|2).
“density” är en metod i vår klass för att beräkna tätheten hos en graf:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Vi kan testa denna metod med följande skript. En komplett graf har en densitet på 1 och en isolerad graf har en densitet på 0, vilket vi kan se av resultaten från föregående testskript:

$ python test_density.py 0.4666666666671.00.0

Kopplade grafer

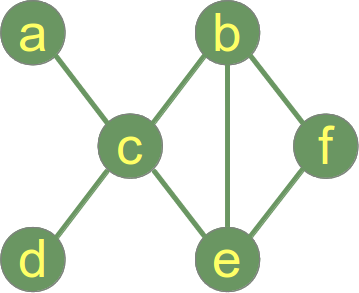En graf sägs vara kopplad om varje par av hörn i grafen är kopplade. Exempelgrafen till höger är en sammanhängande graf.
Det är möjligt att med en enkel algoritm avgöra om en graf är sammanhängande:

1. Välj en godtycklig nod x i grafen G som utgångspunkt
2. Bestäm mängden A av alla noder som kan nås från x.
3. Om A är lika med mängden noder i G är grafen ansluten, annars är den frånkopplad.

Vi implementerar en metod is_connected för att kontrollera om en graf är en ansluten graf. Vi lägger inte vikt vid effektivitet utan vid läsbarhet.
Om du lägger till den här metoden i vår grafklass kan vi testa den med följande skript. Förutsatt att du sparar grafklassen som graph2.py:
En ansluten komponent är en maximalt ansluten undergraf till G. Varje topp hör till exakt en ansluten komponent, liksom varje kant.

Avstånd och diameter i en graf

Avståndet “dist” mellan två toppar i en graf är längden på den kortaste vägen mellan dessa toppar. Inga backtracks, omvägar eller slingor är tillåtna vid beräkningen av ett avstånd.

I vår exempelgraf till höger är avståndet mellan hörnet a och hörnet f 3, dvs. dist(a,f) = 3, eftersom den kortaste vägen går via hörnen c och e (eller alternativt c och b).
Excentriciteten för en topp s i en graf g är det maximala avståndet till varje annan topp i grafen:
e(s) = max( { dist(s,v) | v ∈ V })
(V är mängden av alla toppar i g)
Diametern d i en graf definieras som den maximala excentriciteten för varje topp i grafen. Detta innebär att diametern är längden på den kortaste vägen mellan de mest avlägsna noderna. För att bestämma diametern för en graf ska du först hitta den kortaste vägen mellan varje par hörn. Den största längden på någon av dessa vägar är grafen diameter.
Vi kan direkt se i vår exempelgraf att diametern är 3, eftersom den minsta längden mellan a och f är 3 och det inte finns något annat hörnpar med en längre väg.
Med följande metod implementeras en algoritm för att beräkna diametern. Vi kan beräkna diametern för vår exempelgraf med följande skript, om vi återigen antar att vår kompletta grafklass sparas som graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Det kommer att skriva ut värdet 3.

Den kompletta Python-grafklassen

I följande Python-kod finns den kompletta Python-klassmodulen med alla de diskuterade metoderna:graph2.py

Träd/skog

Ett träd är en oinriktad graf som inte innehåller några cykler. Detta innebär att två hörn i grafen är förbundna med varandra genom exakt en enkel väg.
En skog är en disjunkter union av träd. I motsats till skogar i naturen kan en skog i grafteori bestå av ett enda träd!
En graf med en topp och ingen kant är ett träd (och en skog).
Ett exempel på ett träd: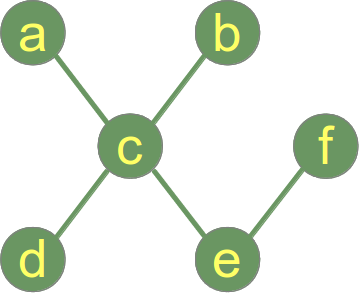

Men medan det föregående exemplet visar en graf som är ett träd och en skog, visar följande bild en graf som består av två träd, dvs.D.v.s. grafen är en skog men inte ett träd:

Översikt över skogar:

Med en topp:

Skogsgrafer med två toppar:

Skogsgrafer med tre hörn:

Skogsgrafer med tre hörn:

Träd med spännvidd

Ett träd med spännvidd T i en sammanhängande, odirigerad graf G är en undergraf G’ till G, som är ett träd, och G’ innehåller alla hörn och en delmängd av kanterna i G. G’ innehåller alla kanter i G, om G är en trädgraf. Informellt sett är ett spännande träd i G ett urval av kanter i G som bildar ett träd som spänner över varje hörn. Det vill säga, varje topp ligger i trädet, men inga cykler (eller slingor) ingår.
Exempel:
En helt sammanhängande graf: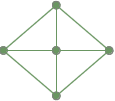

Två överspännande träd från den tidigare helt sammanhängande grafen: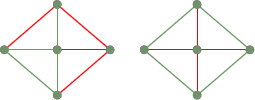

Hamiltonian Game

En Hamiltonstig är en stig i en oriktad eller riktad graf som besöker varje hörn exakt en gång. En Hamiltoncykel (eller krets) är en Hamiltonbana som är en cykel.
Anteckning för datavetare: Det är i allmänhet inte möjligt att avgöra om det finns sådana banor eller cykler i godtyckliga grafer, eftersom det har visat sig att problemet med Hamiltons banor är NP-komplett.
Det är uppkallat efter William Rowan Hamilton, som uppfann det så kallade “icosian game”, eller Hamiltons pussel, som går ut på att hitta en Hamiltons cykel i dodekaederns kantgraf. Hamilton löste detta problem med hjälp av den icosianska kalkylen, en algebraisk struktur baserad på enhetsrötter med många likheter med kvaternionerna, som han också uppfann.

Komplett listning av Graph-klassen

Vi kan testa Graph-klassen med följande program:Om vi startar programmet får vi följande utdata:
Fotnoter:
1 De grafer som studeras i grafteori (och i det här kapitlet i vår Python-handledning) ska inte förväxlas med graferna för funktioner
2 En singleton är en mängd som innehåller exakt ett element.
Krediter:
Narayana Chikkam, nchikkam(at)gmail(dot)com, påpekade ett indexfel i metoden “erdoes_gallai”. Tack så mycket, Narayana!