6.3 Tronätverk
Begreppet villkorligt oberoende kan användas för att ge en kortfattad representation av många områden. Tanken är att det, givet en slumpmässig variabel X, kan finnas en liten uppsättning variabler som direkt påverkar variabelns värde i den meningen att X är villkorligt oberoende av andra variabler givet värden för de direkt påverkande variablerna. Uppsättningen av lokalt påverkande variabler kallas Markov-blanketten. Det är denna lokalitet som utnyttjas i ett trossäkerhetsnätverk. Ett trossamhälle är en riktad modell av villkorligt beroende mellan en uppsättning slumpvariabler. Den exakta förklaringen av villkorligt oberoende i ett belief network tar hänsyn till riktningen.
För att definiera ett belief network börjar man med en uppsättning slumpvariabler som representerar modellens alla egenskaper. Antag att dessa variabler är {X1,…,Xn}.Välj sedan en total ordning av variablerna, X1,…,Xn.
Kedjeregeln (Proposition 6.3) visar hur man kan sönderdela en konjunktion i ovillkorliga sannolikheter:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Och, i termer av slumpvariabler och sannolikhetsfördelningar,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definiera föräldrarna till slumpvariabeln Xi, skrivetparents(Xi), som en minimal mängd föregångare till Xi i den totala ordningsföljden så att de andra föregångarna till Xi är villkorligt oberoende av Xi givetparents(Xi). Det vill säga, föräldrar(Xi) ⊆{X1,…,Xi-1} så att
P(Xi|Xi-1…X1) = P(Xi|föräldrar(Xi)).
Om det finns mer än en minimal mängd kan vilken minimal mängd som helst väljas som föräldrar. Det kan finnas mer än en minimal uppsättning endast när vissa av föregångarna är deterministiska funktioner av andra.
Vi kan sätta ihop kedjeregeln och definitionen av föräldrar, vilket ger
P(X1, X2,—, Xn) = ∏i=1n P(Xi|parents(Xi)).
Sannolikheten över alla variabler, P(X1, X2,—,Xn), kallas den gemensamma sannolikhetsfördelningen. Ett trossamband definierar en faktorisering av den gemensamma sannolikhetsfördelningen, där de betingade sannolikheterna bildar faktorer som multipliceras med varandra.
Ett trossamband, även kallat Bayesiannätverk, är en acyklisk riktad graf (DAG), därnoderna är slumpmässiga variabler. Det finns en båge från varje element iparents(Xi) till Xi.Till nätverket hör en uppsättning villkorliga sannolikhetsfördelningar – den villkorliga sannolikheten för varje variabel med tanke på dess föräldrar (vilket inkluderar de tidigare sannolikheterna för de variabler som inte har några föräldrar).
Sålunda består ett trossamhällsnät av
- en DAG, där varje nod är märkt med en slumpmässig variabel;
- en domän för varje slumpmässig variabel; och
- en uppsättning villkorliga sannolikhetsfördelningar som ger P(X|föräldrar(X)) för varje variabel X.
Ett trossamhällsnät är acykliskt genom konstruktionen. Det sätt på vilket kedjebeslutet sätter samman konjunktionen ger ordningen. En variabel kan endast ha föregångare som föräldrar.Olika dekompositioner kan resultera i olika trossamband.
Antag att vi använder följande variabler, som alla är booleska, i följande ordning:
- Tampering är sant när larmet har manipulerats.
- Brand är sant när det brinner.
- Larm är sant när larmet ljuder.
- Rök är sant när det finns rök.
- Lämnande är sant om det finns många människor som lämnar byggnaden på en gång.
- Rapport är sant om någon rapporterar om att människor lämnar byggnaden. Report är falsk om det inte finns någon rapport om att folk lämnar byggnaden.
Variabeln Report betecknar sensorns rapport om att folk lämnar byggnaden. Denna information är otillförlitlig eftersom den person som ger en sådan rapport kan spela ett skämt, eller så kan ingen som kunde ha gett en sådan rapport ha varit uppmärksam. Denna variabel införs för att möjliggöra konditionering av opålitliga sensordata. Agenten vet vad sensorn rapporterar, men har bara opålitliga bevis om att personer lämnar byggnaden.Som en del av domänen kan man anta följande villkorliga oberoende:
- Brand är villkorligt oberoende av manipulering (givet att ingen annan information finns).
- Larm är beroende av både brand och manipulering. Det vill säga, vi gör inga självständighetsantaganden om hur larm beror på sina föregångare med tanke på denna variabelordning.
- Rök beror endast på brand och är villkorligt oberoende av sabotage och larm med tanke på om det finns en brand eller inte.
- Lämnande beror endast på larm och inte direkt på brand, sabotage eller rök. Det vill säga, att lämna är villkorligt oberoende av de andra variablerna givet larm.
- Rapport beror bara direkt på att lämna.
Trohetsnätverket i figur 6.1 uttrycker dessa beroenden.
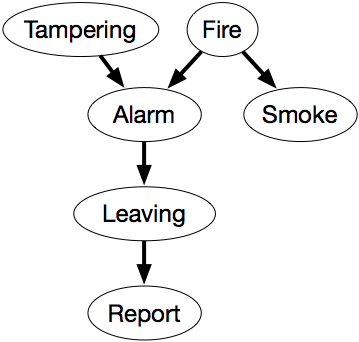
Detta nätverk representerar faktoriseringen
P(Tampering,Fire,Alarm,Smoke,Leaving,Rapport) = P(Tampering) ×P(Fire) ×P(Alarm|Tampering,Fire) ×P(Smoke|Fire) ×P(Leaving|Alarm) ×P(Report|Leaving).
Vi måste också definiera domänen för varje variabel. Anta att variablerna är boolska, det vill säga att de har domänen {true,false}. Vi använder den lilla varianten av variabeln för att representera det sanna värdetoch använder negation för det falska värdet. Exempelvis skrivs Tampering=true som tampering och Tampering=false som ¬tampering.
I exemplen som följer antas följande villkorade sannolikheter:
P(brand) = 0,01
P(larm | brand ∧tampering) = 0.5
P(larm | brand ∧¬trampning) = 0,99
P(larm | ¬brand ∧trampning) = 0,85
P(larm | ¬brand ∧¬trampning) = 0,0001
P(rök | brand ) = 0.9
P(rök | ¬brand ) = 0,01
P(avgång | larm) = 0,88
P(avgång | ¬larm ) = 0,001
P(rapport | avgång ) = 0,75
P(rapport | ¬avgång ) = 0.01
- För varje ledning wi finns det en slumpmässig variabel, Wi, meddomän {livad,död}, som anger om det finns ström i ledningen wi. Wi=liv innebär att ledningenwi har ström. Wi=död innebär att det inte finns någon ström i tråd wi.
- Outside_power med domänen {live,dead} anger om det finns ström som kommer in i byggnaden.
- För varje strömbrytare si anger variabeln Si_pos positionen försi. Den har domänen {up,down}.
- För varje brytare si anger variabeln Si_st tillståndet för brytaren si. Den har domänen {ok,uppochnedvänt,kort,intermittent,trasig}. Si_st=ok innebär att switch si fungerar normalt. Si_st=uppside_down betyder att switchsi är installerad upp och ner. Si_st=kort betyder att brytaren si är förkortad och fungerar som en tråd. Si_st=bruten betyder att strömbrytaren si är trasig och inte tillåter att elektricitet flödar.
- För varje brytarecbi har variabeln Cbi_st domänen {on,off}. Cbi_st=on betyder att strömmen kan flöda genom cbi och Cbi_st=off betyder att strömmen inte kan flöda genom cbi.
- För varje lampa li anger variabeln Li_st med domänen {ok,intermittent,trasig} lampans tillstånd. Li_st=ok betyder att ljuset li tänds om det är strömförsörjt, Li_st=intermittent betyder att ljuset li tänds med jämna mellanrum om det är strömförsörjt och Li_st=bruten betyder att ljuset li inte fungerar.
Låt oss välja en ordning där orsakerna till en variabel står före variabeln i ordningen. Till exempel kommer variabeln för om en lampa är tänd efter variablerna för om lampan fungerar och om det finns ström i lampan.
Om lampan l1 är tänd beror endast på om det finns ström i ledningen w0 och om lampan l1 fungerar som den ska. Andra variabler, t.ex. läget för strömbrytaren s1, om lampan l2 är tänd eller vem som är Kanadas drottning, är irrelevanta. Föräldrarna till L1_lit är således W0 och L1_st.
Tänk på variabeln W0, som representerar om det finns ström i ledningen w0. Om vi visste om det fanns ström i ledningarna w1 ochw2, och om vi kände till ställningen på strömbrytaren s2 och om strömbrytaren fungerade som den skulle, skulle värdet på de andra variablerna (förutomL1_lit) inte påverka vår övertygelse om huruvida det finns ström i ledningen w0. Därför bör föräldrarna till W0 vara S2_Pos, S2_st, W1 och W2.
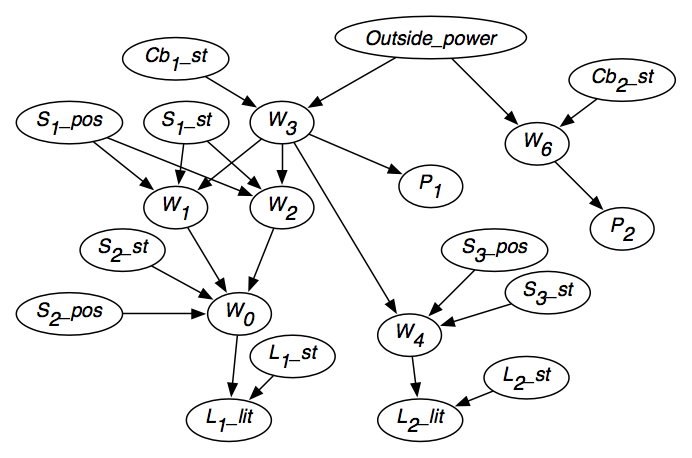
Figur 6.2 visar det resulterande trosnätverket efter det att varje variabels oberoende har beaktats.Trosnätverket innehåller också variablernas domäner, som anges i figuren, och betingade sannolikheter för varje variabel givet dess föräldrar.
För variabeln W1 måste följande villkorliga sannolikheter anges:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=livad|S1_pos=nedåt ∧S1_st=bruten ∧W3=död).
Det finns två värden för S1_pos, fem värden för S1_ok och två värden för W3, så det finns 2×5 ×2 = 20 olika fall där ett värde för W1=livad måste anges. När det gäller sannolikhetsteori kan sannolikheten för W1=live för dessa 20 fall tilldelas godtyckligt. Naturligtvis begränsar kunskapen om området vilka värden som är rimliga. Värdena för W1=död kan beräknas från värdena för W1=levande för vart och ett av dessa fall.
Eftersom variabeln S1_st inte har några föräldrar kräver den en tidigare fördelning, som kan specificeras som sannolikheterna för alla utom ett av värdena; det återstående värdet kan härledas från begränsningen att alla sannolikheter summerar till 1. För att specificera fördelningen av S1_st måste alltså fyra av följande fem sannolikheter specificeras:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Ett trossamhällsnätverk är en grafisk representation av villkorligt oberoende.Oberoendet gör det möjligt för oss att skildra direkta effekter inom grafenoch föreskriver vilka sannolikheter som måste specificeras. Godtyckliga efterföljande sannolikheter kan härledas från nätverket.
Oberoendeantagandet som är inbäddat i ett trohetsnätverk är följande: Varje slumpvariabel är villkorligt oberoende av sina icke efterkommande variabler med tanke på dessföräldrar. Det vill säga, om X är en slumpvariabel med föräldrarna Y1,…, Yn, är alla slumpvariabler som inte är ättlingar till X villkorligt oberoende av X givet Y1,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
om R inte inbegriper någon ättling till X. I den här definitionen inbegriper vi X som en ättling till sig själv. Den högra sidan av denna ekvation är formen för de sannolikheter som specificeras som en del av trosnätverket.R kan involvera X:s förfäder och andra noder så länge de inte är ättlingar till X. Enligt antagandet om oberoende fångas allt inflytande från variabler som inte är ättlingar genom att man känner till värdet av X:s förfäder.
Ofta hänvisar vi bara till den märkta DAG:n som ett trosnätverk. När detta görs är det viktigt att komma ihåg att en domän för varje variabel och en uppsättning villkorliga sannolikhetsfördelningar också ingår i nätverket.
Antalet sannolikheter som måste specificeras för varje variabel är exponentiellt med antalet föräldrar till variabeln.Oberoendeantagandet är användbart om antalet variabler som direkt påverkar en annan variabel är litet. Du bör ordna variablerna så att noderna har så få föräldrar som möjligt.
Tronätverk och kausalitet
Tronätverk har ofta kallats för kausalnätverk och har hävdats vara en bra representation av kausalitet.Kom ihåg att en kausalmodell förutspår resultatet av ingrepp.Antag att du har i åtanke en kausalmodell av en domän där domänen specificeras i termer av en uppsättning slumpmässiga variabler. För varje par slumpvariabler X1och X2, om det finns ett direkt kausalt samband från X1 till X2 (dvs. om ett ingripande för att ändra X1 i något sammanhang med andra variabler påverkar X2 och detta inte kan modelleras genom att ha någon ingripande variabel), lägg till en båge från X1 till X2. Man skulle förvänta sig att kausalmodellen skulle följa trosnätverkets antagande om oberoende. Således skulle alla slutsatser i trosnätverket vara giltiga.
Du skulle också förvänta dig att en sådan graf skulle vara acyklisk; du vill inte att något så småningom ska orsaka sig självt. Detta antagande är rimligt om man beaktar att de slumpmässiga variablerna representerar särskilda händelser snarare än händelsetyper. Tänk till exempel på en orsakskedja som innebär att “vara stressad” får dig att “arbeta ineffektivt”, vilket i sin tur får dig att “vara stressad”. För att bryta den uppenbara cykeln kan vi representera “att vara stressad” i olika skeden som olika slumpvariabler som hänvisar till olika tidpunkter. Att vara stressad i det förflutna gör att du inte arbetar bra för tillfället, vilket gör att du blir stressad i framtiden. Variablerna bör uppfylla tydlighetsprincipen och ha en väldefinierad innebörd. Variablerna bör inte ses som händelsetyper.
Troende-nätverket i sig har inget att säga om orsakssamband, och det kan representera icke-kausalt oberoende, men det verkar särskilt lämpligt när det finns orsakssamband i ett område. Om man lägger till bågar som representerar lokal kausalitet tenderar man att få ett litet trosnätverk. Tronätet i figur 6.2 visar hur detta kan göras för en enkel domän.
Akausala nätverksmodeller för interventioner. Om någon på konstgjord väg skulle tvinga en variabel att ha ett visst värde skulle variabelns efterkommande – men inga andra noder – påverkas. Slutligen kan du se hur kausaliteten i trosnätverk förhåller sig till de kausala och bevismässiga resonemang som diskuteras i avsnitt 5.7. Ett kausalt trosnätverk kan ses som ett sätt att axiomatisera i en kausal riktning. Resonemang i trosnätverk motsvarar att man avleder till orsaker och sedan förutsäger från dessa. Det finns en direkt koppling mellan den logiskt baserade abduktiva syn som diskuteras i avsnitt 5.7 och trosnätverk: Tronätverk kan modelleras som logiska program med sannolikheter över möjliga hypoteser. Detta beskrivs i avsnitt 14.3.
Notera begränsningen “varje slumpvariabel är villkorligt oberoende av sina icke efterkommande variabler givet dessföräldrar” i definitionen av det oberoende som är kodat i ett trossamhällsnätverk. OmR innehåller en efterträdare till variabeln X är antagandet om oberoende inte direkt tillämpligt.
Variabeln S1_pos har inga föräldrar. Det oberoende som är inbäddat i trosnätverket anger således att P(S1_pos=up|A) =P(S1_pos=up) för varje A som inte involverar en ättling tillS1_pos. Om A inbegriper en ättling till S1_pos=up – till exempel om A är S2_pos=up∧L1_lit=true – kan antagandet om oberoende inte tillämpas direkt.
Detta nätverk kan användas på flera sätt:
- Då det här nätverket villkorar kunskapen om att strömbrytarna och brytarna är okej och om värdena för den yttre strömmen och strömbrytarnas läge kan det här nätverket simulera hur belysningen ska fungera.
- Givet värden för den yttre strömmen och ställningen av brytarna kan nätverket härleda sannolikheten för varje utfall – till exempel hur troligt det är att l1 är tänd.
- Givet värden för strömbrytarna och huruvida lamporna är tända kan den efterföljande sannolikheten för att varje strömbrytare eller strömbrytare befinner sig i ett visst tillstånd härledas.
- Givet vissa observationer kan nätverket användas för att resonera baklänges för att bestämma strömbrytarnas mest sannolika läge.
- Givet vissa switchpositioner, vissa utgångar och vissa mellanvärden kan nätverket användas för att bestämma sannolikheten för någon annanvariabel i nätverket.
Ett trossamhälleligt nätverk specificerar en gemensam sannolikhetsfördelning från vilken godtyckliga villkorliga sannolikheter kan härledas. Ett nätverk kan frågas ut genom att man frågar efter den betingade sannolikheten för alla variabler som är betingade av värdena för alla andra variabler. Detta görs vanligtvis genom att tillhandahålla observationer av vissa variabler och fråga efter en annan variabel.
P(brand) = 0,01
P(rapport ) = 0,028
P(rök) = 0.0189
Observation av rapporten ger följande:
P(brand |rapport)= 0,2305
P(rök |rapport) = 0,215
Som väntat ökar sannolikheten för både tampering ochbrand meddenna rapport. Eftersom brand ökar, ökar också sannolikheten för rök.
Antag istället att rök observerades:
P(brand|rök) = 0,476
P(rapport |rök) = 0,320
Bemärk att sannolikheten för tampering inte påverkas av att man observerar rök; däremot ökar sannolikheten för rapport och brand.
Antag att både rapport och rök observerades:
P(brand |rapport ∧rök) = 0,964
Observation av båda gör brand ännu mer sannolik. I samband med rapporten gör dock närvaron av rök det mindre troligt med manipulering. Detta beror på att rapporten förklaras bort av branden, som nu är mer sannolik.
Antag istället att rapporten, men inte röken, observerades:
P(brand|rapport ∧¬rök) = 0,0294
I samband med rapporten blir branden mycket mindre sannolik och sothe sannolikheten för tampering ökar för att förklara rapporten.
Det här exemplet illustrerar hur trosnettensoberoendeantagande ger commonsense-slutsatser och visar också hur bortförklaring är en konsekvens av ett trosnettsoberoendeantagande.
- 6.3.1 Att konstruera trosnätverk