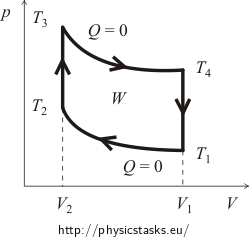
I början är det vanligtvis nödvändigt att få en uppfattning om cykelns pV-diagram. För detta kommer vi att spåra kurvorna för de isokoriska och adiabatiska processerna. Det ungefärliga diagrammet för Otto-cykeln visas i följande figur.
Cykelns verkningsgrad η definieras som
\
där W är det arbete som utförs av gasen under en cykel minus det arbete som utförs av de yttre krafterna (i diagrammet representeras det av ytan av det område som definieras av cykelns linjer!) och Qsup är den värme som tillförs systemet under cykeln.
Arbetet W kan beräknas med hjälp av förhållandet mellan trycket och volymen under en adiabatisk expansion och kompression (det arbete som utförs under en isokorisk process är naturligtvis noll). I den här uppgiften blir det dock bättre att använda det faktum att den totala förändringen av den inre energin per cykel måste vara lika med noll (vi återgår till samma tillstånd som i början, därför förblir temperaturen och därmed den inre energin densamma!). Enligt termodynamikens första lag kan det arbete som utförs av gasen uttryckas som skillnaden mellan den tillförda värmen Qsup och den frigjorda värmen Qrel. Formeln för cykelns verkningsgrad är därför i form av
\
Först ska vi beräkna den tillförda värmen Qsup. Det är uppenbart att under den adiabatiska processen sker inget värmeutbyte och under den isokoriska kylningen avges värme. Detta innebär att värmen tillförs endast under den isokoriska uppvärmningen från temperaturen T2 till temperaturen T3. Mängden av denna värme kan uttryckas i variablerna mängden ämne n i gasen och dess molära värmekapacitet CV på följande sätt:
\
Vi kommer att uttrycka mängden av den frigjorda värmen Qrel på ungefär samma sätt. Vi vet redan att värmen frigörs endast under den isokoriska nedkylningen från temperaturen T4 tillbaka till den ursprungliga temperaturen T1. Det är sant att:
\
Nu sätter vi in dessa formler i formeln för cykelns verkningsgrad och vi får omedelbart:
\ \ \
Nu måste vi uttrycka temperaturskillnaderna genom att använda det givna kompressionsförhållandet
\
och Poissonkvoten κ.
För att göra detta kommer vi att använda ekvationen för en idealgas som genomgår en adiabatisk process (Poissons lag) pVκ = C = konst.., där C är en konstant. Nu utvärderar vi trycket utifrån tillståndsekvationen för en idealgas
\
som vi ersätter med Poissons lag. Nu överför vi konstanterna (C och K) till den ena sidan
\
Nu tillämpar vi denna Poissons lag för båda de adiabatiska processerna. För den adiabatiska expansionen får vi sambandet
\
Och för den adiabatiska kompressionen får vi
\
Nu subtraherar vi den andra ekvationen från den första och faktoriserar ut V1κ – 1 på ena sidan och V2κ – 1 på den andra. Vi får:
\ \ \
Vi kan se att vi faktiskt har lyckats uttrycka temperaturskillnaderna genom att använda de givna värdena. Nu sätter vi in detta förhållande i formeln för verkningsgraden och får den slutliga ekvationen:
\ \ \ \.