av Evan Ma

(handledare i matematik och fysik vid The Edge Learning Center)

Den logaritmiska funktionen verkar förvirra många elever som studerar IB Math SL-programmet. För att förstå den ordentligt, låt oss definiera

där , ett strikt positivt reellt tal, kallas basen och är potensen. Vi kan till exempel alla följande utantill:

och så vidare. Den logaritmiska funktionen gör det omvänt – med ett tal som argument ger den potensen med förbehåll för en angiven bas, och därför definieras den på följande sätt.

Om

då

Därmed står det klart att

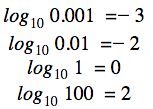
och så vidare. Låt oss titta på andra exempel som involverar andra baser:

Låt oss besvara följande frågor som övning: (a) , (b) , (c) , (d) . Svaren finns i slutet av den här bloggen.

Utifrån definitionen av logaritmen kan vi också se att om vi höjer basen med bas-logaritmen för ett reellt tal får vi tillbaka talet , viz

Du kan försöka verifiera detta genom att använda din miniräknare för olika giltiga baser. Denna identitet är viktig när vi försöker lösa logaritmiska ekvationer, som vi kommer att ge exempel på alter.

Nu ska vi ta en titt på logaritmens regler. I likhet med definitionen av logaritmen använder vi indexets lagar för att härleda reglerna:

1. Logaritmen av en produkt är summan av logaritmerna

Bevis: Säg och , därför

2. Bas- logaritmen av Mr är gånger

Bevis: En produkts logaritm är gånger

: Säg , därför

3. Logaritmen av en kvot är skillnaden mellan logaritmer

Bevis: Säg och , därför

4. Den sista regeln kallas för formel för byte av bas. Vi ska använda ett exempel som verktyg för att härleda formeln. Låt oss säga att vi vill veta vilken potens 2 måste höjas för att få 50. Eftersom 50 inte är en heltalspotens av 2 är svaret inte särskilt uppenbart. Därför skriver vi

och därför. För att hitta säger vi att vi tillämpar bas-10 logaritm på båda sidor av ekvationen eftersom vår miniräknare kanske inte har logaritmtangenten för bas-2:

Korrigerat till 4 signifikanta siffror är värdet på ungefär 5,644. Du kan faktiskt verifiera ditt svar genom att höja 2 till potensen av 5,644 för att se att svaret är ungefär 50.

För att generalisera problemet kan vi säga att vi måste hitta så att och bas- logaritmen inte står till vårt förfogande, kan vi därför istället använda base- logaritm enligt ekvationen

och därför

Som exempel kan vi betrakta följande. Anta att ett belopp på 10 000 dollar sätts in till en ränta på 2,5 procent per år, med årlig uppräkning. Hur länge måste pengarna stå på kontot för att de ska växa till 50 000 dollar?

För att besvara frågan försöker vi i princip hitta n så att

Som min enkla vetenskapliga miniräknare tillåter mig inte att ange en bas av 1.025 för den logaritmiska nyckeln måste jag förlita mig på formeln för byte av bas och använda bas 10, och därmed

Då räntan sätts upp årligen kommer det att ta 66 år att växa minst 5 gånger.

Med tanke på att vi har utforskat logaritmereglerna introducerar vi den naturliga logaritmiska funktionen, eller . Den är bas-, där är det eminenta irrationella talet ≈2,71828 och vars betydelse inom vetenskap och matematik inte kan betonas nog. Därför definieras bas-logaritmen på följande sätt:

Om

då

Nästan ska vi ta en titt på två exempel där vanliga misstag görs när man löser ekvationer med logaritmer. Se om du kan identifiera misstaget.

Var är misstaget? Titta närmare. I det andra steget kan man naturligtvis inte “dela” logaritmen över additionstecknet. Kom ihåg att man bara kan “dela” en logaritm till en summa om logaritmen tillämpas på en produkt, inte en summa. De korrekta stegen är därför följande:

Nu ska vi titta på följande exempel och se om du kan identifiera felet:

Var är felet? Ja, det är i det andra steget – en kvot av logaritmer är naturligtvis inte logaritmen av kvoten. Vi kan snarare använda formeln för byte av bas för att förenkla det första steget på följande sätt:

Slutligt ska vi illustrera hur vi kan använda logaritmens regler för att lösa följande:

Du kanske lägger märke till att den okända förekommer som basen och som en variabel i logaritmens argument. Hur kan vi lösa ? Metoden är fortfarande beroende av att logaritmens regler tillämpas konsekvent. Först höjer vi båda sidorna som potenser av basen , och därmed

Du kanske minns från definitionen av logaritmen att den vänstra sidan bara blir logaritmens argument, och därför

Genom att ordna om ovanstående ekvation behöver vi lösa

Om vi märker att detta liknar en kvadratisk i , löser vi på följande sätt:

Nu, var är den negativa roten? Eftersom också är basen för logaritmen förkastas därför den negativa roten som lösning. Därför är det slutliga svaret.

Med hjälp av ovanstående exempel kan du se att det inte alls är svårt att lösa en till synes svår logaritmisk ekvation – det räcker med att tillämpa logaritmens regler konsekvent för att få fram den rätta lösningen.

Svar på frågor: (a) 2 (b) 3 (c) -3 (d) -2.