Kolmogorov-Smirnov-test
K-S-testet är ett test för god överensstämmelse som används för att bedöma likformigheten hos en uppsättning datafördelningar. Det utformades som ett svar på bristerna i chi-kvadrat-testet, som endast ger exakta resultat för diskreta, indelade fördelningar. K-S-testet har den fördelen att det inte gör några antaganden om hur de datamängder som skall jämföras är indelade, vilket undanröjer den godtyckliga karaktär och informationsförlust som följer med processen för val av bin.
Inom statistiken är K-S-testet det accepterade testet för att mäta skillnader mellan kontinuerliga datamängder (oinning av datafördelningar) som är en funktion av en enda variabel. Detta differensmått, K-S \(D\)-statistiken, definieras som det maximala värdet av den absoluta skillnaden mellan två kumulativa fördelningsfunktioner. Det ensidiga K-S-testet används för att jämföra en datamängd med en känd kumulativ fördelningsfunktion, medan det tvåsidiga K-S-testet jämför två olika datamängder. Varje uppsättning data ger en annan kumulativ fördelningsfunktion, och dess betydelse ligger i dess förhållande till den sannolikhetsfördelning från vilken datamängden är hämtad: sannolikhetsfördelningsfunktionen för en enda oberoende variabel \(x\) är en funktion som tilldelar varje värde av \(x\) en sannolikhet. Den sannolikhet som det specifika värdet \(x_{i}\) har är värdet av sannolikhetsfördelningsfunktionen vid \(x_{i}\) och betecknas \(P(x_{i})\).Den kumulativa fördelningsfunktionen definieras som den funktion som anger andelen datapunkter till vänster om ett givet värde \(x_{i}\), \(P(x <x_{i})\); den representerar sannolikheten för att \(x\) är mindre än eller lika med ett visst värde \(x_{i}\).
För att jämföra två olika kumulativa fördelningsfunktioner \(S_{N1}(x)\) och \(S_{N2}(x)\) är K-S-statistiken
D = max|S_N1(x) – S_N2(x)|
där \(S_{N}(x)\) är den kumulativa fördelningsfunktionen för den sannolikhetsfördelning från vilken en datauppsättning med \(N\) händelser dras. Om \(N\) ordnade händelser finns vid datapunkterna \(x_{i}\), där \(i = 1, \ldots, N\), så
S_N(x_i) = (i-N)/N
där datamatrisen \(x\) är sorterad i stigande ordning. Detta är en stegfunktion som ökar med \(1/N\) vid värdet av varje ordnad datapunkt.
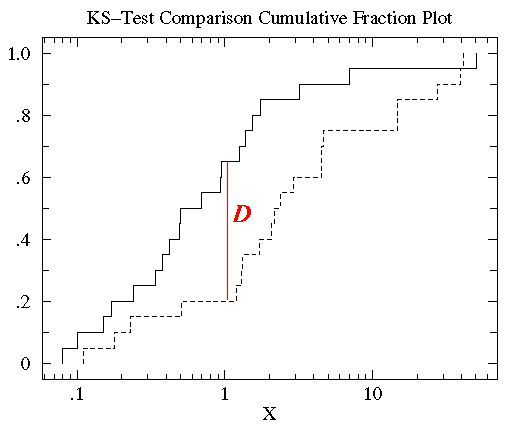
Kirkman, T.W. (1996) Statistists to Use.
http://www.physics.csbsju.edu/stats/
För våra syften är de två fördelningar som jämförs den uppmätta fördelningen av ankomsttiderna och den ackumulerade fraktionen på det förflutna tidsintervallet. Om nollhypotesen (ingen variabilitet) gäller, får vi 50 % av händelserna på 50 % av den förflutna tiden, och statistiken \(D\) bör fördela sig enligt Kolmogorovfördelningen för många realiseringar av fördelningen av ankomsttiderna. Den sannolikhet som testet ger är således \(p_{KS} = 1 – \alpha\), där \(\alpha\) är sannolikheten (enligt Kolmogorovfördelningen) för att värdet av \(D\) är större eller lika med det uppmätta värdet. Ett litet värde på \(p_{KS}\) indikerar därför överensstämmelse med nollhypotesen, medan ett stort värde på \(p_{KS}\) indikerar att intervallet mellan händelserna inte är konstant, och därför kan man dra slutsatsen om variabilitet.