StatsTest Flow: Förutsägelse >> Kontinuerlig beroende variabel >> Mer än en oberoende variabel >> Inga upprepade mätningar >> En beroende variabel
Är du inte säker på att detta är rätt statistisk metod? Använd arbetsflödet Choose Your StatsTest för att välja rätt metod.
- Vad är multivariat multipel linjär regression?
- Antaganden för multivariat multipel linjär regression
- Linearitet
- Inga outliers
- Samma spridning över intervallet
- Normalitet för residualer
- Ingen multikollinearitet
- När man ska använda multivariat multipel linjär regression?
- Förutsägelse
- Kontinuerlig beroende variabel
- Mer än en oberoende variabel
- Multivariat multipel linjär regression Exempel
- Fler ställda frågor
- Hjälp!
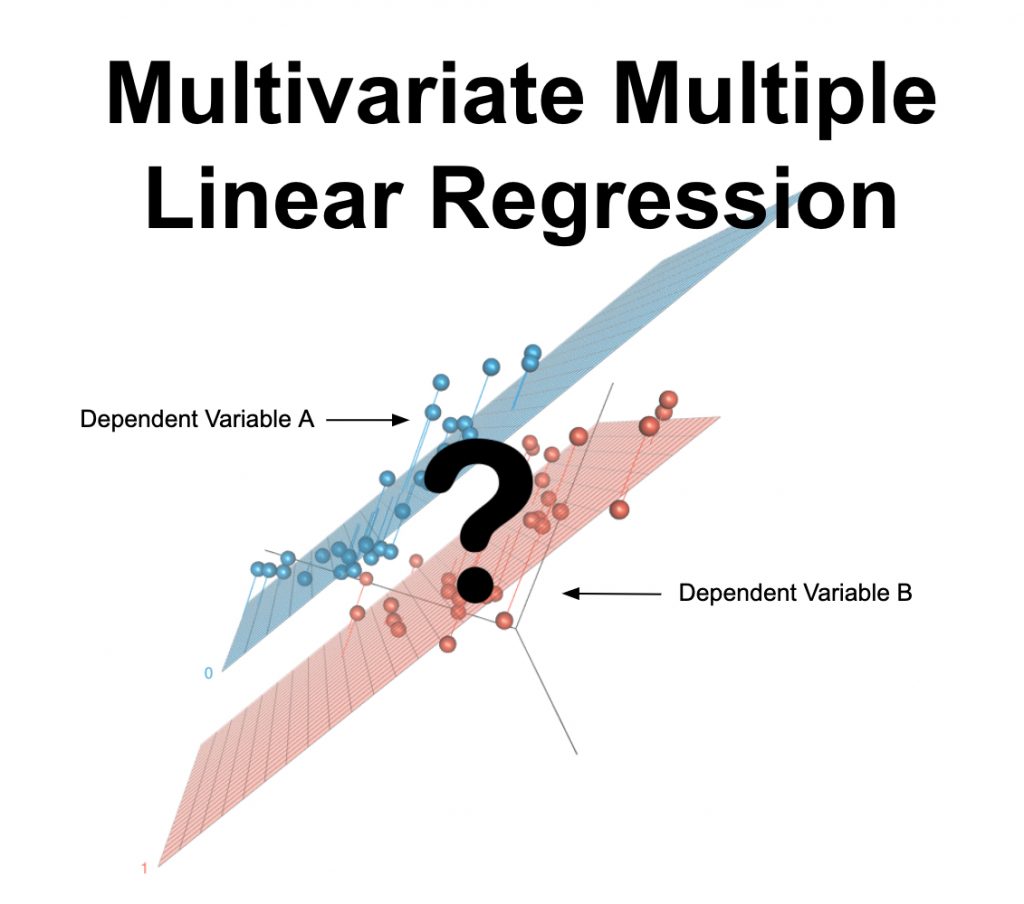
Vad är multivariat multipel linjär regression?
Multivariat multipel linjär regression är ett statistiskt test som används för att förutsäga flera utfallsvariabler med hjälp av en eller flera andra variabler. Det används också för att fastställa det numeriska förhållandet mellan dessa uppsättningar av variabler och andra. Variabeln som du vill förutsäga ska vara kontinuerlig och dina data ska uppfylla de andra antaganden som anges nedan.
Antaganden för multivariat multipel linjär regression
Alla statistiska metoder har antaganden. Antaganden innebär att dina data måste uppfylla vissa egenskaper för att resultaten av den statistiska metoden ska vara korrekta.
Antagandena för multivariat multipel linjär regression omfattar:
- Linearitet
- Inga outliers
- Samma spridning över hela intervallet
- Normalitet för residualer
- Ingen multikollinearitet
Låtsas vi dyka in i var och en av dessa separat.
Linearitet
De variabler som du bryr dig om måste ha ett linjärt samband. Det innebär att om du plottar variablerna ska du kunna dra en rak linje som passar dataformen.
Inga outliers
De variabler som du bryr dig om får inte innehålla outliers. Linjär regression är känslig för outliers, eller datapunkter som har ovanligt stora eller små värden. Du kan se om dina variabler har outliers genom att plotta dem och observera om några punkter ligger långt ifrån alla andra punkter.
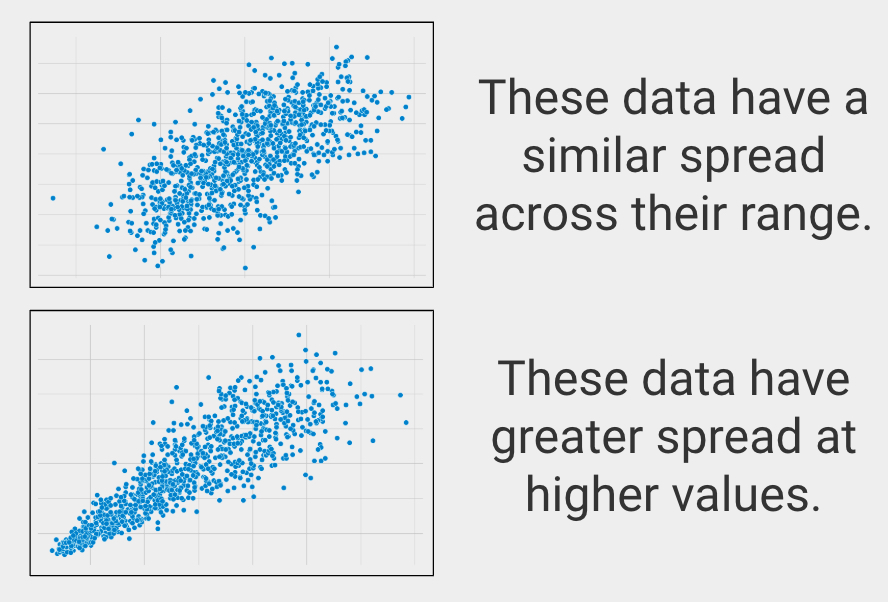
Samma spridning över intervallet
I statistiken kallas detta för homoscedasticitet, vilket beskriver när variabler har en liknande spridning över sina intervall.
Normalitet för residualer
Med ordet “residualer” avses de värden som uppstår när man subtraherar de förväntade (eller förutspådda) beroende variablerna från de faktiska värdena. Fördelningen av dessa värden bör motsvara en normal (eller klockkurva) distributionsform.
Om detta antagande uppfylls säkerställs att resultaten av regressionen är lika tillämpliga över hela spridningen av data och att det inte finns någon systematisk bias i förutsägelsen.
Ingen multikollinearitet
Multikollinearitet hänvisar till scenariot när två eller flera av de oberoende variablerna är väsentligt korrelerade sinsemellan. När multikollinearitet förekommer blir regressionskoefficienterna och den statistiska signifikansen instabila och mindre trovärdiga, även om det inte påverkar hur väl modellen passar data i sig.
När man ska använda multivariat multipel linjär regression?
Du bör använda multivariat multipel linjär regression i följande scenario:
- Du vill använda en variabel i en förutsägelse av flera andra variabler, eller du vill kvantifiera det numeriska förhållandet mellan dem
- Variablerna du vill förutsäga (din beroende variabel) är kontinuerliga
- Du har mer än en oberoende variabel, eller en variabel som du använder som prediktor
- Du har inga upprepade mätningar från samma observationsenhet
- Du har mer än en beroende variabel
Låt oss förtydliga dessa för att hjälpa dig att veta när du ska använda multivariat multipel linjär regression.
Förutsägelse
Du letar efter ett statistiskt test för att förutsäga en variabel med hjälp av en annan. Detta är en fråga om förutsägelse. Andra typer av analyser är att undersöka styrkan i förhållandet mellan två variabler (korrelation) eller att undersöka skillnader mellan grupper (skillnad).
Kontinuerlig beroende variabel
Den variabel du vill förutsäga måste vara kontinuerlig. Kontinuerlig innebär att din variabel av intresse i princip kan anta vilket värde som helst, t.ex. hjärtfrekvens, längd, vikt, antal glassbitar du kan äta på en minut osv.
Typer av data som INTE är kontinuerliga är bland annat ordnade data (t.ex. slutplacering i ett lopp, bästa företagsranking osv.), kategoriska data (kön, ögonfärg, ras osv.) eller binära data (har köpt produkten eller inte, har sjukdomen eller inte osv.).
Om din beroende variabel är binär bör du använda multipel logistisk regression, och om din beroende variabel är kategorisk bör du använda multinomial logistisk regression eller linjär diskriminantanalys.
Mer än en oberoende variabel
Multivariat multipel linjär regression används när det finns en eller flera prediktorvariabler med flera värden för varje observationsenhet.
Ingen upprepade åtgärder
Denna metod lämpar sig för scenariot när det endast finns en observation för varje observationsenhet. Observationsenheten är det som utgör en “datapunkt”, t.ex. en butik, en kund, en stad osv.
Om du har en eller flera oberoende variabler men de mäts för samma grupp vid flera tidpunkter bör du använda en modell med blandade effekter.
Mer än en beroende variabel
För att köra multivariat multipel linjär regression bör du ha mer än en beroende variabel, eller variabel som du försöker förutsäga.
Om du bara förutsäger en variabel bör du använda multipel linjär regression.
Multivariat multipel linjär regression Exempel
Dependent variabel 1: Intäkter
Dependentvariabel 2: Kundtrafik
Oberoende variabel 1: Dollar som spenderas på reklam per stad
Oberoende variabel 2: Befolkning per stad
Nollhypotesen, som är statistisk jargong för vad som skulle hända om behandlingen inte gör någonting, är att det inte finns något samband mellan utgifter för reklam och reklampengar eller befolkning per stad. Vårt test kommer att bedöma sannolikheten för att denna hypotes är sann.
Vi samlar in våra data och efter att ha försäkrat oss om att antagandena för linjär regression är uppfyllda utför vi analysen.
Denna analys utför i praktiken multipel linjär regression två gånger med hjälp av båda de beroende variablerna. När vi kör analysen får vi alltså betakoefficienter och p-värden för varje term i modellen “intäkter” och i modellen “kundtrafik”. För alla linjära regressionsmodeller har du en betakoefficient som är lika med interceptet för din linjära regressionslinje (ofta märkt med ett 0 som β0). Det är helt enkelt där regressionslinjen korsar y-axeln om du skulle plotta dina data. Vid multipel linjär regression finns det dessutom två fler fler andra betakoefficienter (β1, β2 osv.) som representerar förhållandet mellan de oberoende och beroende variablerna.
Dessa ytterligare betakoefficienter är nyckeln till att förstå det numeriska förhållandet mellan dina variabler. I huvudsak förväntas din beroende variabel förändras med värdet av den betakoefficient som är kopplad till den oberoende variabeln (samtidigt som andra oberoende variabler hålls konstanta) för varje enhetsökning (värde 1) av en given oberoende variabel.
P-värdet som är kopplat till dessa ytterligare betavärden är chansen att se våra resultat om man antar att det faktiskt inte finns något samband mellan den variabeln och intäkterna. Ett p-värde som är mindre än eller lika med 0,05 innebär att vårt resultat är statistiskt signifikant och att vi kan lita på att skillnaden inte enbart beror på slumpen. För att få ett övergripande p-värde för modellen och enskilda p-värden som representerar variablernas effekter i de två modellerna används ofta MANOVAs.
Den här analysen kommer dessutom att resultera i ett R-kvadratvärde (R2). Detta värde kan variera från 0-1 och representerar hur väl din linjära regressionslinje passar dina datapunkter. Ju högre R2-värdet är, desto bättre passar modellen in på data.
Fler ställda frågor
Q: Vad är skillnaden mellan multivariat multipel linjär regression och att köra linjär regression flera gånger?
A: De är begreppsmässigt likartade, eftersom de enskilda modellkoefficienterna kommer att vara desamma i båda scenarierna. En väsentlig skillnad är dock att signifikanstester och konfidensintervall för multivariat linjär regression tar hänsyn till de flera beroende variablerna.
Q: Hur kör jag multivariat multipel linjär regression i SPSS, R, SAS eller STATA?
A: Den här resursen är inriktad på att hjälpa dig att välja rätt statistisk metod varje gång. Det finns många resurser som kan hjälpa dig att ta reda på hur du ska köra den här metoden med dina data:
R-artikel: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/
Hjälp!
Om du fortfarande inte kommer på något är du välkommen att kontakta oss.