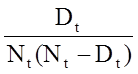Det finns flera olika sätt att skatta en överlevnadsfunktion eller en överlevnadskurva. Det finns ett antal populära parametriska metoder som används för att modellera överlevnadsdata, och de skiljer sig åt när det gäller de antaganden som görs om fördelningen av överlevnadstider i befolkningen. Några populära fördelningar är exponential-, Weibull-, Gompertz- och lognormalfördelningen.2 Den kanske mest populära är exponentialfördelningen, som utgår från att en deltagares sannolikhet att drabbas av den aktuella händelsen är oberoende av hur länge personen har varit händelselös. Andra fördelningar gör olika antaganden om sannolikheten för att en person ska drabbas av en händelse (dvs. den kan öka, minska eller förändras över tiden). Mer information om parametriska metoder för överlevnadsanalys finns i Hosmer och Lemeshow och Lee och Wang1,3.

Vi fokuserar här på två icke-parametriska metoder, som inte gör några antaganden om hur sannolikheten att en person utvecklar händelsen förändras över tiden. Med hjälp av icke-parametriska metoder uppskattar och plottar vi överlevnadsfördelningen eller överlevnadskurvan. Överlevnadskurvor plottas ofta som stegfunktioner, vilket visas i figuren nedan. Tiden visas på X-axeln och överlevnaden (andelen personer i riskzonen) visas på Y-axeln. Observera att den procentuella andelen deltagare som överlever inte alltid motsvarar den procentuella andelen som lever (vilket förutsätter att det intressanta utfallet är döden). “Överlevnad” kan också avse andelen som är fria från en annan utfallshändelse (t.ex. procentandel fria från hjärtinfarkt eller kardiovaskulär sjukdom), eller så kan det också representera procentandelen som inte upplever ett hälsosamt utfall (t.ex. cancerremiss).

Överlevnadsfunktion

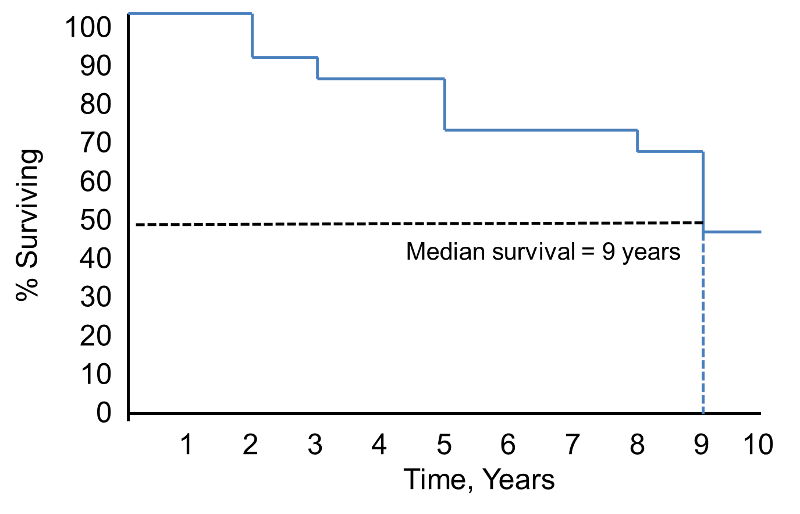
Bemärk att överlevnadssannolikheten är 100 % under 2 år och sedan sjunker till 90 %. Medianöverlevnaden är 9 år (dvs. 50 % av befolkningen överlever 9 år; se streckade linjer).

Exempel:

Tänk på en liten prospektiv kohortstudie som är utformad för att studera tiden till döden. Studien omfattar 20 deltagare som är 65 år och äldre; de registreras under en femårsperiod och följs i upp till 24 år tills de dör, studien avslutas eller de hoppar av studien (förlorad uppföljning). Uppgifterna visas nedan. I studien finns det 6 dödsfall och 3 deltagare med fullständig uppföljning (dvs. 24 år). De återstående 11 deltagarna har färre än 24 års uppföljning på grund av sen registrering eller förlust av uppföljning.

Deltagarnas identifikationsnummer	Dödsår	År Senaste kontakt
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Livstabell (aktuariell tabell)

Ett sätt att sammanfatta deltagarnas erfarenheter är med en livstabell, eller en försäkringsteknisk tabell. Livstabeller används ofta inom försäkringsbranschen för att uppskatta den förväntade livslängden och fastställa premier. Vi fokuserar på en särskild typ av livstabell som används flitigt i biostatistiska analyser och som kallas kohortlivstabell eller uppföljningslivstabell. Uppföljningslivstabellen sammanfattar deltagarnas erfarenheter under en fördefinierad uppföljningsperiod i en kohortstudie eller i en klinisk prövning fram till tidpunkten för den intressanta händelsen eller slutet av studien, beroende på vad som inträffar först.

För att konstruera en livstabell organiserar vi först uppföljningstiderna i intervall med lika stort avstånd. I tabellen ovan har vi en maximal uppföljningstid på 24 år, och vi överväger 5-årsintervall (0-4, 5-9, 10-14, 15-19 och 20-24 år). Vi summerar antalet deltagare som lever i början av varje intervall, antalet som dör och antalet som censureras i varje intervall.

Intervall i år	Antal som lever i början av intervallet	Antal som avlider under intervallet	Antal som censureras
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

Vi använder följande notation i vår livstidsanalys. Vi definierar först notationen och använder den sedan för att konstruera livstabellen.

• Nt = antal deltagare som är händelselösa och anses vara i riskzonen under intervallet t (t.ex, i detta exempel antalet levande eftersom vårt utfall av intresse är död)
• Dt = antal deltagare som dör (eller drabbas av den händelse som är av intresse) under intervall t
• Ct = antal deltagare som censureras under intervall t Nt* = genomsnittligt antal deltagare som är i riskzonen under intervall t
• Nt* = genomsnittligt antal deltagare som är i riskzonen under intervall t [När man konstruerar försäkringstekniska livstabeller gör man ofta följande antaganden: För det första antas de intressanta händelserna (t.ex. dödsfall) inträffa i slutet av intervallet och de censurerade händelserna antas inträffa jämnt (eller jämnt) under hela intervallet. Därför görs ofta en justering av Nt för att återspegla det genomsnittliga antalet deltagare i riskzonen under intervallet, Nt*, som beräknas på följande sätt: Nt* = Nt-Ct/2 (dvs, vi subtraherar hälften av de censurerade händelserna).
• qt = andelen som dör (eller drabbas av en händelse) under intervallet t, qt = Dt/Nt*
• pt = andelen som överlever (förblir händelselös) intervallet t, pt = 1-qt
• St, andelen som överlever (eller förblir händelselös) efter intervallet t; detta kallas ibland kumulativ överlevnadssannolikhet och beräknas på följande sätt: För det första definieras andelen deltagare som överlever efter tidpunkt 0 (starttidpunkten) som S0 = 1 (alla deltagare lever eller är händelselösa vid tidpunkt noll eller studiestart). Andelen som överlever efter varje efterföljande intervall beräknas med hjälp av principer för villkorlig sannolikhet som introducerades i modulen om sannolikhet. Sannolikheten för att en deltagare överlever efter intervall 1 är S1 = p1. Sannolikheten för att en deltagare överlever efter intervall 2 innebär att de måste överleva efter intervall 1 och genom intervall 2: S2 = P(överleva efter intervall 2) = P(överleva genom intervall 2)*P(överleva efter intervall 1), eller S2 = p2*S1. I allmänhet är St+1 = pt+1*St.

För det första intervallet, 0-4 år, visas formatet för den uppföljande livstabellen nedan.

För det första intervallet, 0-4 år: Vid tidpunkt 0, början av det första intervallet (0-4 år), finns det 20 deltagare som lever eller är i riskzonen. Två deltagare dör under intervallet och 1 censureras. Vi tillämpar korrigeringen för antalet censurerade deltagare under det intervallet för att få fram Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Beräkningarna av de övriga kolumnerna visas i tabellen. Sannolikheten för att en deltagare överlever efter 4 år, eller efter det första intervallet (genom att använda den övre gränsen för intervallet för att definiera tiden) är S4 = p4 = 0,897.

För det andra intervallet, 5-9 år: Antalet riskpersoner är antalet riskpersoner i det föregående intervallet (0-4 år) minus de som dör och censureras (dvs. Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). Sannolikheten att en deltagare överlever efter 9 år är S9 = p9*S4 = 0,937*0,897 = 0,840.

Intervall i år	Antal i riskzonen under intervallet, Nt	Genomsnittligt antal i riskzonen under intervallet, Nt*	Antal dödsfall under intervallet, Dt	Förlorad uppföljning, Ct	Andel som dör under intervallet, qt	Andel som överlever bland riskgrupperna Intervall, pt	Sannolikhet för överlevnad St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

Den kompletta uppföljningslivstabellen visas nedan.

Intervall i år	Antal i riskzonen under intervallet, Nt	Genomsnittligt antal i riskzonen under intervallet, Nt*	Antal dödsfall under intervallet, Dt	Förlorad uppföljning, Ct	Andel som dör Under intervallet, qt	Am Among Those at Risk, Andel som överlever Intervall, pt	Överlevnadssannolikhet St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Denna tabell använder den aktuariella metoden för att konstruera tabellen för uppföljningslivslängd där tiden är uppdelad i lika stora intervall.

Kaplan-Meier (Product Limit) Approach

Ett problem med livstabellmetoden som visas ovan är att överlevnadssannolikheterna kan förändras beroende på hur intervallen är organiserade, särskilt med små urval. Kaplan-Meier-metoden, även kallad produktgränsmetoden, är en populär metod som löser detta problem genom att överlevnadssannolikheten omvärderas varje gång en händelse inträffar.

En lämplig användning av Kaplan-Meier-metoden vilar på antagandet att censurering är oberoende av sannolikheten att utveckla den aktuella händelsen och att överlevnadssannolikheterna är jämförbara för deltagare som rekryteras tidigt och senare i studien. När man jämför flera grupper är det också viktigt att dessa antaganden uppfylls i varje jämförelsegrupp och att t.ex. censurering inte är mer sannolik i en grupp än i en annan.

I tabellen nedan används Kaplan-Meier-metoden för att presentera samma data som presenterades ovan med hjälp av livscykelmetoden. Observera att vi börjar tabellen med Tid=0 och Överlevnadssannolikhet = 1. Vid Tid=0 (baslinjen, eller studiens början) är alla deltagare i riskzonen och överlevnadssannolikheten är 1 (eller 100 %). Med Kaplan-Meier-metoden beräknas överlevnadssannolikheten med hjälp av St+1 = St*((Nt+1-Dt+1)/Nt+1). Observera att beräkningarna med Kaplan-Meier-metoden liknar beräkningarna med den försäkringstekniska livstabellmetoden. Den största skillnaden är tidsintervallen, dvs. med den aktuariella livstabellmetoden tar vi hänsyn till jämnt fördelade intervaller, medan vi med Kaplan-Meiermetoden använder observerade händelsetider och censureringstider. Beräkningarna av överlevnadssannolikheterna beskrivs i detalj i de första raderna i tabellen.

Livstabell med Kaplan-Meier-metoden

Tid, År	Antal i riskzonen Nt	Antal dödsfall Dt	Antal censurerat Ct	Sannolikhet för överlevnad St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20				1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3		3	0.507

Med stora datamängder är dessa beräkningar omständliga. Dessa analyser kan dock genereras av statistiska beräkningsprogram som SAS. Excel kan också användas för att beräkna överlevnadssannolikheterna när data organiseras efter tidpunkter och antalet händelser och censurerade tidpunkter sammanfattas.

Från livstabellen kan vi ta fram en Kaplan-Meier överlevnadskurva.

Kaplan-Meier överlevnadskurva för uppgifterna ovan

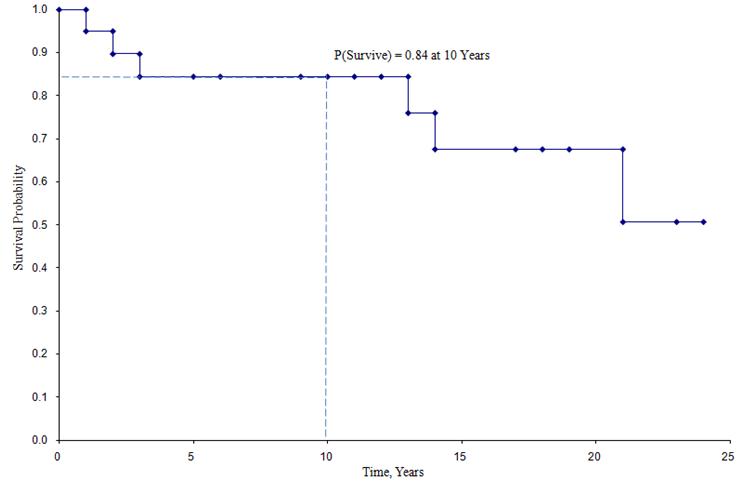
I överlevnadskurvan ovan representerar symbolerna varje händelsetid, antingen ett dödsfall eller en censurerad tid. Utifrån överlevnadskurvan kan vi också uppskatta sannolikheten för att en deltagare överlever efter 10 år genom att lokalisera 10 år på X-axeln och läsa uppåt och över till Y-axeln. Andelen deltagare som överlever efter 10 år är 84 % och andelen deltagare som överlever efter 20 år är 68 %. Medianöverlevnaden uppskattas genom att placera 0,5 på Y-axeln och läsa över och ner till X-axeln. Medianöverlevnaden är ungefär 23 år.

Standardfel och konfidensintervallskattningar av överlevnadssannolikheter

Dessa skattningar av överlevnadssannolikheter vid specifika tidpunkter och medianöverlevnadstiden är punktskattningar och bör tolkas som sådana. Det finns formler för att producera standardfel och konfidensintervallskattningar av överlevnadssannolikheter som kan genereras med många statistiska datapaket. En populär formel för att uppskatta standardfelet för överlevnadsskattningarna kallas Greenwoods5 formel och är följande:

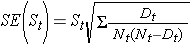
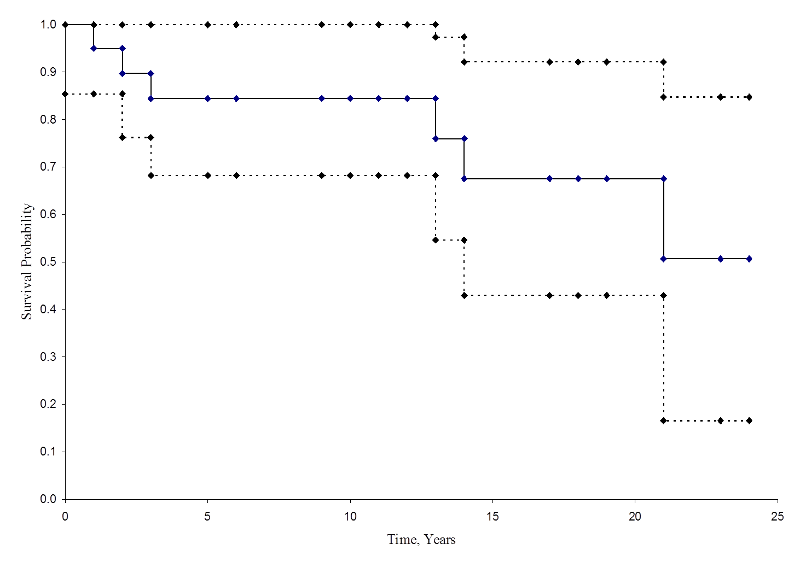
Mängden 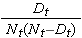summeras för antal risktagare (Nt) och antal dödsfall (Dt) som inträffat fram till och med den aktuella tidpunkten (dvs. kumulativt, över alla tidpunkter före den aktuella tidpunkten, se exempel i tabellen nedan). Standardfel beräknas för överlevnadsskattningarna för uppgifterna i tabellen nedan. Observera att den sista kolumnen visar kvantiteten 1,96*SE(St) som är felmarginalen och används för att beräkna 95 % konfidensintervallsskattningar (dvs. St ± 1,96 x SE(St)).

Standardfel för överlevnadsskattningar

Tid, År	Antal i riskzonen Nt	Antal dödsfall Dt	överlevnad Sannolikhet St				1.96*SE (St)
0	20		1
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0,000	0,118	0,174	0,341

Figuren nedan sammanfattar skattningarna och konfidensintervallen i figuren nedan. Kaplan-Meier överlevnadskurvan visas som en heldragen linje och 95 % konfidensgränserna visas som streckade linjer.

Kaplan-Meier överlevnadskurva med konfidensintervall

Kumulativa incidenskurvor

Vissa utredare föredrar att generera kumulativa incidenskurvor, till skillnad från överlevnadskurvor som visar de kumulativa sannolikheterna för att drabbas av den aktuella händelsen. Kumulativ incidens, eller kumulativ misslyckandesannolikhet, beräknas som 1-St och kan enkelt beräknas från livstabellen med hjälp av Kaplan-Meier-metoden. De kumulativa sannolikheterna för misslyckande för exemplet ovan visas i tabellen nedan.

Livstabell med kumulativa sannolikheter för misslyckande

Tid, År	Antal i riskzonen Nt	Antal dödsfall Dt	Antal Censurerade Ct	Sannolikhet för överlevnad St	Sannolikhet för misslyckande 1-St
0	20				1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0,493

Figuren nedan visar den kumulativa incidensen av dödsfall för deltagare som ingick i den ovan beskrivna studien.

Kumulativ incidenskurva

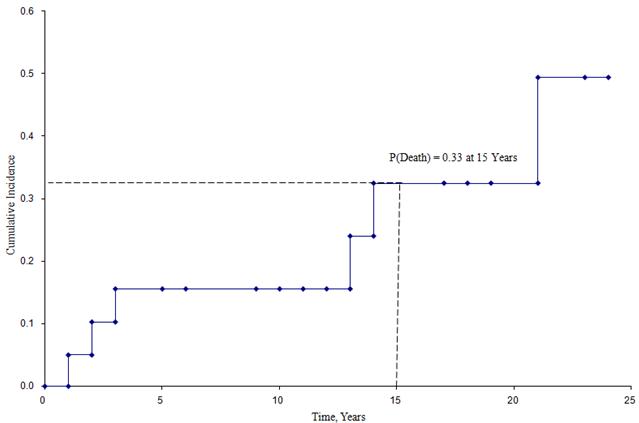
Utifrån denna figur kan vi uppskatta sannolikheten att en deltagare dör vid en viss tidpunkt. Exempelvis är sannolikheten för dödsfall ungefär 33 % vid 15 år (se streckade linjer).

Tillbaka till början | föregående sida | nästa sida