|
Vad är en Tetraeder?
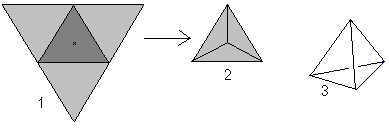
Om man tittar på ordet tetraeder (tetraeder betyder “med fyra plan”) kan man kalla varje pyramid med en triangel som bas för en tetraeder.
Hursomhelst är tetraedern den raka, regelbundna triangelpyramiden på den här webbplatsen.
Tetraedrontoppens delar
Höjd och area för en sidotriangel
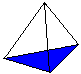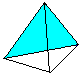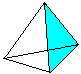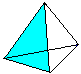
Fyra liksidiga trianglar bildar en tetraeder.
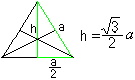 … … |
En triangel plockas ut: De tre höjderna skär varandra i en punkt som i alla trianglar. Detta är triangelns mittpunkt. Höjden kan beräknas utifrån sidan a som h=sqr(3)/2*a med hjälp av Pythagoras sats. |
Höjderna är också medianer och skär varandra i förhållandet2:1. Det används i följande beräkningar.
Triangelns area är A=sqr(3)/4*a².
Rymdhöjd
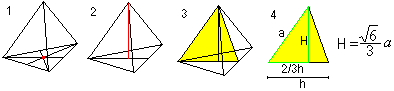
Centrum, omskriven sfär och inskriven sfär
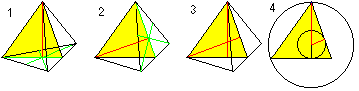
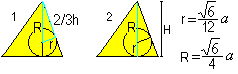 … … |
Du får två formler för r och R med hjälp av Pythagoras sats (1) och H=R+r (2): Det är r=sqr(6)/12*a , R=sqr(6)/4*a. |
Vinkelyta
…. 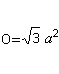 ….. ….. |
Som yta av basen och sidoytorna bildar ytanO. Det finns O=4*A (triangel) = sqr(3)a². |
Volym

Tetraediska tal topp
…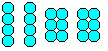 … … |
Om man limmar ihop 20 kulor till två grupper med fyra och två med sex får man ett välkänt pussel: Man måste bilda en pyramid med fyra delar. |
Det finns många liknande pussel.
Tetraeder i kuben topp
Sex diagonaler på ytan bildar en tetraeder i kuben.
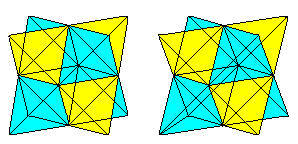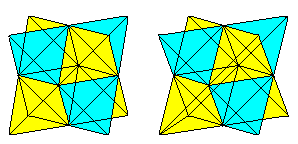
Om du kan 3D-bilden kan du tredimensionellt betrakta följande två kubpar.
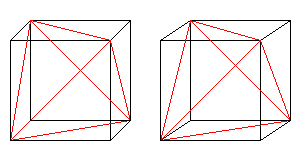
Om du ritar en andra tetraeder och skärningslinjerna får du en penetration av två tetraedrar.
Figuren består av ansiktsdiagonalerna och förbindelselinjerna för centrumen av de laterala rutorna i den ursprungliga kuben. De sista bildar en oktaeder.
Ringar av tetraedrar top
Du kan göra papperstetraedrar och klistra ett jämnt antal av dem till en ring. Ringen kan hela tiden vrida sig inåt eller utåt genom centrum. Detta är en vacker leksak. – Dessa ringar kallas också för kaleidocyklar.Du hittar mer på min webbsida Kaleidocyklar.
Tetraeder på Internetuppehåll
Tyska
Christof Weber
Washat dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)
Albert Kluge
Einrotierender Tetraeder als Java-Applet
FAZ
Tetraederpackung:Eins geht noch
Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)
Gerd Müller
PlatonischeKörper in Stereodarstellung
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder
LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder
ruhr-guide
TetraederBottrop
Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl
Engelska
Eric W. Weisstein (World of Mathematics)
Tetraeder
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder
Joyce Frost och Peg Cagle (mathforum)
En fantastisk, rymdfyllande, oregelbunden Tetraeder
Wikipedia
Tetraeder,Tetrapod(struktur), Tetraedertal