Práce je definována jako energie, kterou přidáme objektu působením síly F na určitou vzdálenost r.

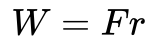
To může znamenat např. zvednutí objektu na vzdálenost r proti gravitaci. Přidaná energie je pak potenciální energií. V tomto případě však chci ukázat, jak souvisí práce s kinetickou energií.

Působíte-li na předmět silou, aby se pohyboval rychleji, zvyšujete jeho kinetickou energii.

Jak spolu souvisí, ukážu na jedné z pohybových rovnic, kterou jsem se zabýval dříve.

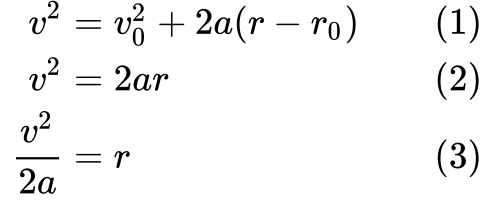
Začneme definicí (1) a pak ji zjednodušíme (2) tím, že počáteční rychlost v₀ a počáteční uražená vzdálenost r₀ jsou obě nulové.

Nakonec rovnici (3) přeuspořádáme tak, abychom získali způsob vyjádření r, který můžeme dosadit do W = Fr.

Z rovnice chceme také odstranit zrychlení, protože výraz pro kinetickou energii ho neobsahuje. Přestavíme si druhý Newtonsův zákon:

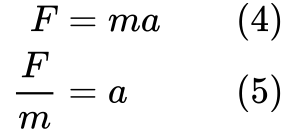
Nyní máme kousky k odvození rovnice pro kinetickou energii.

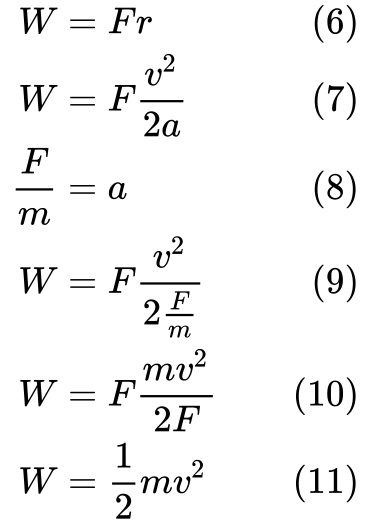
(7) dosadíme r do rovnice (3). Pak můžeme nahradit a v rovnici (9) definicí pro zrychlení v rovnici (8).

Nakonec (11) vidíme, že práce se rovná kinetické energii.

Když jsem si náhodou znovu pročítal tento příspěvek, všiml jsem si, že můj postup mohl být mnohem jednodušší.

Pokud začneme s W = Fv²/2a a F = ma, pak místo a dosadíme přímo F a dostaneme W = mav²/2a. Pak a snadno odstraníme a dostaneme W = mv²/2.