Christian Bohr og begrebet cooperative bindingRediger

I 1904 studerede Christian Bohr hæmoglobinbinding til ilt under forskellige betingelser. Ved at plotte hæmoglobinmætning med ilt som en funktion af iltpartialtrykket fik han en sigmoidal (eller “S-formet”) kurve. Dette viser, at jo mere ilt er bundet til hæmoglobin, jo lettere er det for mere ilt at binde sig – indtil alle bindingssteder er mættet. Bohr bemærkede desuden, at stigende CO2-tryk forskød denne kurve mod højre – dvs. at højere koncentrationer af CO2 gør det sværere for hæmoglobin at binde ilt. Sidstnævnte fænomen er sammen med observationen af, at hæmoglobins affinitet for ilt stiger med stigende pH, kendt som Bohr-effekten.

Original figur fra Christian Bohr, der viser den sigmoide stigning af oxyhæmoglobin som funktion af iltpartialtrykket.

Et receptormolekyle siges at udvise kooperativ binding, hvis dets binding til ligand skalerer ikke-lineært med ligandkoncentrationen. Cooperativitet kan være positiv (hvis binding af et ligandmolekyle øger receptorens tilsyneladende affinitet og dermed øger chancen for, at et andet ligandmolekyle binder sig) eller negativ (hvis binding af et ligandmolekyle mindsker affiniteten og dermed gør binding af andre ligandmolekyler mindre sandsynlig). Den “fraktionelle belægning” Y ¯ {\displaystyle {\bar {\bar {Y}}}

af en receptor med en given ligand defineres som mængden af ligand-bundne bindingssteder divideret med den samlede mængde af ligand-bindingssteder: Y ¯ = + = {\displaystyle {\bar {Y}}}={{\frac {}{+}}}}={\frac {}{}{}}}}

Hvis Y ¯ = 0 {\displaystyle {\bar {Y}}}=0}

, så er proteinet fuldstændig ubundet, og hvis Y ¯ = 1 {\displaystyle {\bar {Y}}}=1}

, er det fuldstændig mættet. Hvis plottet af Y ¯ {\displaystyle {\bar {\bar {Y}}}

ved ligevægt som funktion af ligandkoncentrationen er sigmoidalformet, som Bohr observerede det for hæmoglobin, tyder det på positiv kooperativitet. Hvis det ikke er tilfældet, kan man ikke udtale sig om kooperativitet ved at se på dette plot alene.

Begrebet kooperativ binding gælder kun for molekyler eller komplekser med mere end ét ligandbindingssted. Hvis der findes flere ligandbindingssteder, men ligandbinding til et af disse steder ikke påvirker de andre, siges receptoren at være ikke-samarbejdsvillig. Cooperativitet kan være homotropisk, hvis en ligand påvirker bindingen af ligander af samme art, eller heterotropisk, hvis den påvirker bindingen af andre slags ligander. I forbindelse med hæmoglobin observerede Bohr homotrop positiv kooperativitet (binding af ilt letter bindingen af mere ilt) og heterotrop negativ kooperativitet (binding af CO2 reducerer hæmoglobins evne til at binde ilt).)

Igennem det 20. århundrede er der blevet udviklet forskellige rammer til at beskrive bindingen af en ligand til et protein med mere end ét bindingssted og de kooperative virkninger, der observeres i denne sammenhæng.

Hill-ligningenRediger

Den første beskrivelse af kooperativ binding til et protein med flere bindingssteder blev udviklet af A.V. Hill. Med udgangspunkt i observationer af iltbinding til hæmoglobin og ideen om, at kooperativitet skyldes aggregering af hæmoglobinmolekyler, der hver især binder ét iltmolekyle, foreslog Hill en fænomenologisk ligning, som siden er blevet opkaldt efter ham:

Hill-plot af Hill-ligningen i rødt, der viser kurvens hældning som Hill-koefficienten og skæringspunktet med x-aksen, der giver den tilsyneladende dissociationskonstant. Den grønne linje viser den ikke-samarbejdsvillige kurve.

Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {\bar {Y}}}={\frac {K\cdot {}^{n}}}{1+K\cdot {}^{n}}}}={\frac {^{n}}}{K^{*}+^{n}}}={\frac {^{n}}{K_{d}^{n}}+^{n}}}}

hvor n {{\displaystyle n}}

er “Hill koefficienten”, {\displaystyle }

betegner ligandkoncentrationen, K {\displaystyle K}

betegner en tilsyneladende associationskonstant (anvendt i ligningens oprindelige form), K ∗ {\displaystyle K^{*}}

er en empirisk dissociationskonstant, og K d {\displaystyle K_{d}}}

er en mikroskopisk dissociationskonstant (anvendes i moderne former af ligningen og svarer til en E C 50 {\displaystyle \mathrm {EC} _{50}}

). Hvis n < 1 {\displaystyle n<1}

, udviser systemet negativ kooperativitet, mens kooperativiteten er positiv, hvis n > 1 {\displaystyle n>1}

. Det samlede antal ligandbindingssteder er en øvre grænse for n {\displaystyle n}

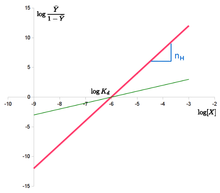
. Hill-ligningen kan lineariseres som: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}}{1-{\bar {Y}}}}=n\cdot {}\\log-n\cdot {}\log K_{d}}

“Hill plot” fås ved at plotte log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {{\bar {Y}}}{1-{\bar {Y}}}}}

versus log {\displaystyle \log}

. I tilfældet med Hill-ligningen er det en linje med hældning n H {\displaystyle n_{H}}

og interceptet log ( K d ) {\displaystyle \log(K_{d})}

. Dette betyder, at kooperativiteten antages at være fast, dvs. at den ikke ændrer sig med mætning. Det betyder også, at bindingsstederne altid udviser den samme affinitet, og at kooperativitet ikke skyldes en affinitet, der stiger med ligandkoncentrationen.

Adair-ligningenRediger

G.S. Adair fandt, at Hill-plottet for hæmoglobin ikke var en lige linje og opstillede den hypotese, at bindingsaffinitet ikke var et fast udtryk, men afhængig af ligandmætning. Efter at have påvist, at hæmoglobin indeholdt fire hemes (og dermed bindingssteder for ilt), arbejdede han ud fra den antagelse, at fuldt mættet hæmoglobin dannes i etaper, med mellemformer med et, to eller tre bundne iltmolekyler. Dannelsen af hvert mellemstadie fra ubundet hæmoglobin kan beskrives ved hjælp af en tilsyneladende makroskopisk associationskonstant K i {\displaystyle K_{i}}

. Den resulterende fraktionelle belægning kan udtrykkes som: Y ¯ = 1 4 ⋅ K I + 2 K I I I 2 + 2 K I I I 2 + 3 K I I I I 3 + 4 K I V 4 1 + K I + K I I I 2 + K I I I I I 3 + K I V 4 {\displaystyle {\bar {Y}}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, for ethvert protein med n ligandbindingssteder:

Y ¯ = 1 n K I + 2 K I I I 2 + … + n K n n n 1 + K I + K I I I 2 + … + K n n n {\displaystyle {\bar {\bar {Y}}}={\frac {1}{n}}}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

hvor n betegner antallet af bindingssteder og hver K i {\displaystyle K_{i}}

er en kombineret associationskonstant, der beskriver bindingen af i ligandmolekyler.Ved at kombinere Adair-behandlingen med Hill-plottet kommer man frem til den moderne eksperimentelle definition af kooperativitet (Hill, 1985, Abeliovich, 2005). Den resulterende Hill-koefficient, eller mere korrekt hældningen af Hill-plottet som beregnet ud fra Adair-ligningen, kan vises at være forholdet mellem variansen af bindingstallet og variansen af bindingstallet i et tilsvarende system af ikke-interagerende bindingssteder. Hill-koefficienten definerer således kooperativitet som en statistisk afhængighed af et bindingssted af tilstanden af et eller flere andre bindingssted(er).

Klotz-ligningenRediger

Irving Klotz, der arbejdede med calciumbindende proteiner, dekonvoluterede Adairs associationskonstanter ved at overveje trinvis dannelse af mellemstadierne og forsøgte at udtrykke den kooperative binding i form af elementære processer styret af massevirkningsloven. Inden for hans rammer er K 1 {\displaystyle K_{1}}}

er den associationskonstant, der styrer bindingen af det første ligandmolekyle, K 2 {\displaystyle K_{2}}}

er den associationskonstant, der styrer bindingen af det andet ligandmolekyle (når det første allerede er bundet) osv. For Y ¯ {\displaystyle {\bar {\bar {Y}}}}

, giver dette: Y ¯ = 1 n K 1 + 2 K 1 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {\displaystyle {\bar {\bar {Y}}}={\frac {1}{n}}}{\frac {K_{1}+2K_{1}K_{2}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Det er værd at bemærke, at konstanterne K 1 {\displaystyle K_{1}}}

, K 2 {\displaystyle K_{2}}}

og så videre vedrører ikke de enkelte bindingssteder. De beskriver, hvor mange bindingssteder der er besat, snarere end hvilke. Denne form har den fordel, at kooperativitet let kan erkendes, når man betragter associationskonstanterne. Hvis alle ligandbindingssteder er identiske med en mikroskopisk associationskonstant K {\displaystyle K}

, vil man forvente, at K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}}}K,\ldots K_{n}={\frac {1}{n}}}}K}

(dvs. K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}}}K}

) i fravær af kooperativitet. Vi har positiv kooperativitet, hvis K i {\displaystyle K_{i}}

ligger over disse forventede værdier for i > 1 {\displaystyle i>1}

.

Klotz-ligningen (som undertiden også kaldes Adair-Klotz-ligningen) anvendes stadig ofte i den eksperimentelle litteratur til at beskrive målinger af ligandbinding i form af sekventielle tilsyneladende bindingskonstanter.

Pauling-ligningenRediger

I midten af det 20. århundrede var der en øget interesse for modeller, der ikke kun beskrev bindingskurver fænomenologisk, men også tilbød en underliggende biokemisk mekanisme. Linus Pauling omfortolkede ligningen leveret af Adair og antog, at hans konstanter var en kombination af bindingskonstanten for liganden ( K { {\displaystyle K}

i ligningen nedenfor) og energi, der kommer fra interaktionen mellem underenhederne i det samarbejdende protein ( α {\displaystyle \alpha }

nedenfor). Pauling udledte faktisk flere ligninger, afhængigt af graden af interaktion mellem underenhederne. På baggrund af forkerte antagelser om lokaliseringen af hemes valgte han den forkerte til at beskrive hæmoglobins iltbinding, idet han antog, at underenhederne var anbragt i et kvadrat. Nedenstående ligning giver ligningen for en tetraedrisk struktur, hvilket ville være mere korrekt i tilfældet med hæmoglobin: Y ¯ = K + 3 α K 2 2 2 + 3 α 3 K 3 3 3 + α 6 K 4 4 4 1 + 4 K + 6 α K 2 2 2 + 4 α 3 K 3 3 3 + α 6 K 4 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alpha {}K^{2}^{2}^{2}+3\alpha {}^{3}K^{3}^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}{1+4K+6\alpha {}K^{2}^{2}^{2}+4\alpha {}^{3}K^{3}^{3}^{3}+\alpha {}^{6}K^{4}^{4}^{4}}}}

KNF-modellenRediger

Baseret på resultater, der viser, at strukturen af kooperative proteiner ændres ved binding til deres ligand, Daniel Koshland og kolleger forfinede den biokemiske forklaring af den mekanisme, som Pauling havde beskrevet. Koshland-Némethy-Filmer-modellen (KNF) går ud fra, at hver underenhed kan eksistere i en af to konformationer: aktiv eller inaktiv. Ligandbinding til en underenhed vil medføre en øjeblikkelig konformationsændring af den pågældende underenhed fra den inaktive til den aktive konformation, en mekanisme, der beskrives som “induced fit”. Ifølge KNF-modellen vil kooperativitet opstå som følge af interaktioner mellem underenhederne, hvis styrke varierer afhængigt af de involverede underenheders relative konformationer. For en tetraedrisk struktur (de overvejede også lineære og kvadratiske strukturer) foreslog de følgende formel:

Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B B ( K X K t ) 2 + 3 K A B 3 K B B B 3 ( K X K t ) 3 + K B B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B B ( K X K t ) 2 + 4 K A B 3 K B B B 3 ( K X K t ) 3 + K B B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Hvor K X {\displaystyle K_{X}}}

er tilknytningskonstanten for X, K t {\displaystyle K_{t}}

er forholdet mellem B- og A-tilstande i fravær af ligand (“overgang”), K A B {\displaystyle K_{AB}}

og K B B {\displaystyle K_{BB}}

er de relative stabiliteter af par af nabounderenheder i forhold til et par, hvor begge underenheder er i A-tilstand (Bemærk, at KNF-papiret faktisk præsenterer N s {\displaystyle N_{s}}}

, antallet af besatte steder, som her er 4 gange Y ¯ {\displaystyle {\bar {Y}}}}

).

MWC-modellenRediger

Monod-Wyman-Changeux-modelreaktionsskemaet for et protein, der består af to protomerer. Protomeren kan eksistere under to tilstande, hver med en forskellig affinitet for liganden. L er forholdet mellem tilstande i fravær af ligand, c er forholdet mellem affiniteterne.

Energiskema af en Monod-Wyman-Changeux-model af et protein bestående af to protomerer. Ligandens større affinitet for R-tilstanden betyder, at sidstnævnte fortrinsvis stabiliseres af bindingen.

Monod-Wyman-Changeux-modellen (MWC) for samordnede allosteriske overgange gik et skridt videre ved at udforske kooperativitet baseret på termodynamik og tredimensionelle konformationer. Den blev oprindeligt formuleret for oligomeriske proteiner med symmetrisk anordnede, identiske underenheder, som hver har ét ligandbindingssted. I henhold til denne ramme eksisterer to (eller flere) indbyrdes konverterbare konformationstilstande af et allosterisk protein i termisk ligevægt. Tilstandene – ofte kaldet spændte (T) og afslappede (R) – adskiller sig fra hinanden med hensyn til affinitet for ligandmolekylet. Forholdet mellem de to tilstande reguleres af bindingen af ligandmolekyler, der stabiliserer den tilstand med højere affinitet. Det er vigtigt, at alle underenheder i et molekyle skifter tilstande på samme tid, et fænomen, der er kendt som “samordnet overgang”.

Den allosteriske isomeriseringskonstant L beskriver ligevægten mellem de to tilstande, når der ikke er bundet noget ligandmolekyle: L = {{\displaystyle L={\frac {\left}{\left}}}

. Hvis L er meget stor, findes det meste af proteinet i T-tilstanden i fravær af ligand. Hvis L er lille (tæt på 1), er R-tilstanden næsten lige så befolket som T-tilstanden. Forholdet mellem dissociationskonstanterne for liganden fra T- og R-tilstandene beskrives ved konstanten c: c = K d R K d T {\displaystyle c={{\frac {K_{d}^{R}}}{K_{d}^{T}}}}

. Hvis c = 1 {\displaystyle c=1}

, har både R- og T-tilstande den samme affinitet for liganden, og liganden påvirker ikke isomeriseringen. Værdien af c angiver også, hvor meget ligevægten mellem T- og R-tilstandene ændres ved ligandbinding: jo mindre c er, jo mere forskydes ligevægten til R-tilstanden efter en binding. Med α = K d R {\displaystyle \alpha ={\frac {}{{K_{d}^{R}}}}

, beskrives den fraktionelle belægning som: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {\bar {Y}}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Det sigmoide Hill plot for allosteriske proteiner kan derefter analyseres som en progressiv overgang fra T-tilstanden (lav affinitet) til R-tilstanden (høj affinitet), efterhånden som mætningen stiger. Hill-plottets hældning afhænger også af mætningen, med en maksimal værdi ved bøjningspunktet. Skæringspunkterne mellem de to asymptoter og y-aksen gør det muligt at bestemme affiniteten af begge tilstande for liganden.

Hill-plot af MWC-bindingsfunktionen i rødt, af den rene T- og R-tilstand i grønt. Efterhånden som konformationen skifter fra T til R, gør bindingsfunktionen det også. Skæringspunkterne med x-aksen giver den tilsyneladende dissociationskonstant samt de mikroskopiske dissociationskonstanter for R- og T-tilstande.

I proteiner er konformationsændringer ofte forbundet med aktivitet eller aktivitet over for specifikke mål. En sådan aktivitet er ofte det, der er fysiologisk relevant eller det, der måles eksperimentelt. Graden af konformationsændring beskrives af tilstandsfunktionen R ¯ {\displaystyle {\bar {\bar {R}}}

, som angiver den fraktion af protein, der er til stede i R {\displaystyle R}}

state. Som energidiagrammet illustrerer, er R ¯ {\displaystyle {\bar {\bar {R}}}

stiger, efterhånden som flere ligandmolekyler bindes. Udtrykket for R ¯ {\displaystyle {\bar {R}}}

er: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}}={\frac {(1+\alpha )^{n}}}{(1+\alpha )^{n}}+L(1+c\alpha )^{n}}}}

Et afgørende aspekt af MWC-modellen er, at kurverne for Y ¯ {\displaystyle {\bar {Y}}}

og R ¯ {\displaystyle {\bar {R}}}

er ikke sammenfaldende, dvs. at fraktionel mætning ikke er en direkte indikator for konformationstilstand (og dermed aktivitet). Desuden kan omfanget af bindingens og aktiveringens kooperativitet være meget forskellige: et ekstremt tilfælde er bakteriernes flagellamotor med en Hill-koefficient på 1,7 for bindingen og 10,3 for aktiveringen. Responsens supra-linearitet kaldes undertiden ultrasensitivitet.

Hvis et allosterisk protein binder til et mål, der også har en højere affinitet for R-tilstanden, så stabiliserer målbindingen yderligere R-tilstanden og øger dermed ligandens affinitet. Hvis et mål på den anden side fortrinsvis binder til T-tilstanden, vil målbinding have en negativ virkning på ligandaffiniteten. Sådanne mål kaldes allosteriske modulatorer.

Siden dens begyndelse er MWC-rammen blevet udvidet og generaliseret. Der er blevet foreslået variationer, f.eks. for at tage højde for proteiner med mere end to tilstande, proteiner, der binder til flere typer af ligander eller flere typer af allosteriske modulatorer, og proteiner med ikke-identiske underenheder eller ligandbindingssteder.