Arbeit ist definiert als die Energie, die man einem Objekt durch Aufbringen einer Kraft F über eine bestimmte Strecke r hinzufügt.

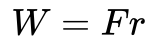
Das kann z.B. bedeuten, dass man ein Objekt gegen die Schwerkraft eine Strecke r hochhebt. Die zugeführte Energie ist dann potentielle Energie. In diesem Fall möchte ich jedoch zeigen, wie die Arbeit mit der kinetischen Energie zusammenhängt.

Wenn man eine Kraft auf ein Objekt ausübt, damit es sich schneller bewegt, erhöht man seine kinetische Energie.

Ich werde zeigen, wie die beiden zusammenhängen, indem ich eine der Bewegungsgleichungen verwende, die ich bereits behandelt habe.

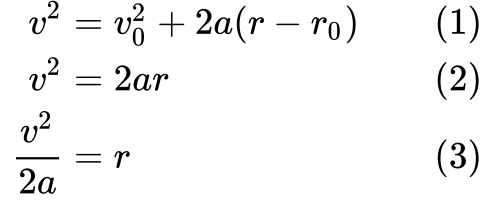
Wir beginnen mit der Definition (1) und vereinfachen sie (2), indem wir sagen, dass die Anfangsgeschwindigkeit v₀ und der anfänglich zurückgelegte Weg r₀ beide Null sind.

Schließlich ordnen wir (3) die Gleichung um, um einen Weg zu finden, r auszudrücken, so dass wir sie in W = Fr einsetzen können.

Wir wollen auch die Beschleunigung aus der Gleichung loswerden, weil der Ausdruck für die kinetische Energie sie nicht enthält. Lasst uns Newtons zweites Gesetz umstellen:

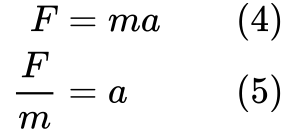
Jetzt haben wir die Teile, um die Gleichung für die kinetische Energie abzuleiten.

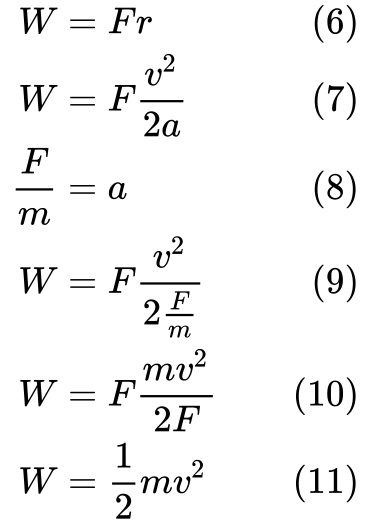
(7) Ersetze r mit Gleichung (3). Dann können wir a in Gleichung (9) mit der Definition für die Beschleunigung in Gleichung (8) ersetzen.

Schließlich (11) können wir sehen, dass Arbeit gleich kinetische Energie ist.

Beim erneuten Durchlesen dieses Beitrags ist mir aufgefallen, dass mein Ansatz viel einfacher hätte sein können.

Wenn wir mit W = Fv²/2a und F = ma beginnen, dann setzen wir F direkt anstelle von a ein und erhalten W = mav²/2a. Dann lässt sich a leicht eliminieren und wir erhalten W = mv²/2.