Christian Bohr ja yhteistoiminnallisen sitoutumisen käsiteEdit

Christian Bohr tutki vuonna 1904 hemoglobiinin sitoutumista happiin eri olosuhteissa. Kun hän piirsi hemoglobiinin kylläisyyden hapella hapen osapaineen funktiona, hän sai sigmoidisen (tai “S-muotoisen”) käyrän. Tämä osoittaa, että mitä enemmän happea on sitoutunut hemoglobiiniin, sitä helpommin lisää happea sitoutuu – kunnes kaikki sitoutumiskohdat ovat kyllästyneet. Lisäksi Bohr huomasi, että hiilidioksidin paineen nousu siirsi tätä käyrää oikealle – eli korkeammat hiilidioksidipitoisuudet vaikeuttavat hemoglobiinin hapen sitoutumista. Tämä jälkimmäinen ilmiö yhdessä sen havainnon kanssa, että hemoglobiinin affiniteetti happea kohtaan kasvaa pH:n noustessa, tunnetaan nimellä Bohrin efekti.

Alkuperäinen Christian Bohrin kuva, jossa näkyy oksyhemoglobiinin sigmoidinen kasvu hapen osapaineen funktiona.

Reseptorimolekyylin sanotaan osoittavan yhteistoiminnallista sitoutumista, jos sen sitoutuminen ligandiin skaalautuu epälineaarisesti ligandin konsentraation mukaan. Yhteistoiminnallisuus voi olla positiivista (jos ligandimolekyylin sitoutuminen lisää reseptorin näennäistä affiniteettia ja siten lisää toisen ligandimolekyylin sitoutumisen todennäköisyyttä) tai negatiivista (jos ligandimolekyylin sitoutuminen vähentää affiniteettia ja siten vähentää muiden ligandimolekyylien sitoutumisen todennäköisyyttä). “Osittainen miehitys” Y ¯ ¯ {\displaystyle {\bar {\bar {Y}}}

reseptorin sitoutuminen tiettyyn ligandiin määritellään ligandiin sitoutuneiden sitoutumiskohtien määränä jaettuna ligandiin sitoutumiskohtien kokonaismäärällä: Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}}={\frac {}{}{}}}}}}

Jos Y ¯ = 0 {\displaystyle {\bar {Y}}=0}

, niin proteiini on täysin sitoutumaton, ja jos Y ¯ = 1 {\displaystyle {\bar {Y}}=1}

, se on täysin kyllästynyt. Jos kuvaaja Y ¯ {\displaystyle {\bar {Y}}}

tasapainotilassa ligandikonsentraation funktiona on muodoltaan sigmoidinen, kuten Bohr havaitsi hemoglobiinille, tämä osoittaa positiivista cooperatiivisuutta. Jos näin ei ole, pelkästään tätä kuvaajaa tarkastelemalla ei voida tehdä mitään johtopäätöksiä yhteistoiminnallisuudesta.

Kooperatiivisen sitoutumisen käsite koskee vain molekyylejä tai komplekseja, joissa on useampi kuin yksi ligandin sitoutumiskohta. Jos ligandin sitoutumiskohtia on useita, mutta ligandin sitoutuminen johonkin kohtaan ei vaikuta muihin, reseptorin sanotaan olevan ei-kooperatiivinen. Yhteistoiminnallisuus voi olla homotrooppista, jos ligandi vaikuttaa samantyyppisten ligandien sitoutumiseen, tai heterotrooppista, jos se vaikuttaa muunlaisten ligandien sitoutumiseen. Hemoglobiinin tapauksessa Bohr havaitsi homotrooppista positiivista yhteistoiminnallisuutta (hapen sitoutuminen helpottaa lisähapen sitoutumista) ja heterotrooppista negatiivista yhteistoiminnallisuutta (hiilidioksidin sitoutuminen vähentää hemoglobiinin kykyä sitoa happea).)

Kautta 1900-luvun on kehitetty erilaisia kehyksiä kuvaamaan ligandin sitoutumista proteiiniin, jolla on useampi kuin yksi sitoutumiskohta, ja tässä yhteydessä havaittuja yhteistoiminnallisia vaikutuksia.

Hillin yhtälöEdit

Ensimmäisen kuvauksen yhteistoiminnallisesta sitoutumisesta useamman kuin yhden sitoutumiskohdan omaavaan proteiiniin kehitti A.V. Hill. Perustuen havaintoihin hapen sitoutumisesta hemoglobiiniin ja ajatukseen, että yhteistoiminnallisuus syntyi hemoglobiinimolekyylien aggregoitumisesta, joista kukin sitoi yhden happimolekyylin, Hill ehdotti fenomenologista yhtälöä, joka on sittemmin nimetty hänen mukaansa:

Hillin yhtälön Hillin kuvaaja punaisella, jossa käyrän kaltevuus on Hillin kerroin ja leikkauspiste x-akselilla antaa näennäisen dissosiaatiovakion. Vihreä viiva osoittaa ei-kooperatiivisen käyrän.

Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {Y}}={\frac {K\cdot {}^{n}}}{1+K\cdot {}^{n}}}}={\frac {^{n}}}{K^{*}+^{n}}}={\frac {^{n}}}{K_{d}^{n}+^{n}}}}

missä n {\displaystyle n}

on “Hillin kerroin”, {\displaystyle}

on “Hillin kerroin”.

tarkoittaa ligandin konsentraatiota, K {\displaystyle K}

tarkoittaa näennäistä assosiaatiovakiota (jota käytetään yhtälön alkuperäisessä muodossa), K ∗ {\displaystyle K^{*}}}

on empiirinen dissosiaatiovakio, ja K d {\displaystyle K_{d}}

mikroskooppinen dissosiaatiovakio (jota käytetään yhtälön nykyaikaisissa muodoissa ja joka vastaa E C 50 {\displaystyle \mathrm {EC} _{50}}

). Jos n < 1 {\displaystyle n<1}

, systeemillä on negatiivinen yhteistoiminnallisuus, kun taas yhteistoiminnallisuus on positiivinen, jos n > 1 {\displaystyle n>1}

. Ligandin sitoutumiskohtien kokonaismäärä on yläraja n {\displaystyle n}

. Hillin yhtälö voidaan linearisoida seuraavasti: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log-n\cdot {\bar {\bar {Y}}}}=n\cdot {\log-n\cdot {\bar {\bar {\bar {Y}}}}=n\cdot {\log-n\cdot {\bar {\bar {\bar {Y}}}}=n\cdot {\bar

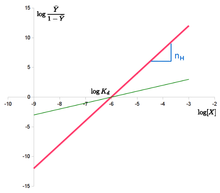
“Hill plot” saadaan piirtämällä log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}}

vastaan log {\displaystyle \log}

. Hillin yhtälön tapauksessa se on viiva, jonka kaltevuus on n H {\displaystyle n_{H}}

ja leikkauspiste log ( K d ) {\displaystyle \log(K_{d})}

. Tämä tarkoittaa, että yhteistoiminnallisuus oletetaan kiinteäksi, eli se ei muutu kyllästymisen myötä. Se tarkoittaa myös sitä, että sitoutumispaikoilla on aina sama affiniteetti, eikä kooperatiivisuus johdu siitä, että affiniteetti kasvaa ligandikonsentraation myötä.

Adairin yhtälöEdit

G.S. Adair havaitsi, että hemoglobiinin Hillin kuvaaja ei ollut suora viiva, ja esitti hypoteesin, että sitoutumisaffiniteetti ei ollut kiinteä termi, vaan riippuvainen ligandin kylläisyydestä. Hän osoitti, että hemoglobiini sisälsi neljä hemiä (ja siten hapen sitoutumiskohtia), ja lähti siitä olettamuksesta, että täysin tyydyttynyt hemoglobiini muodostuu vaiheittain, ja välimuodoissa on yksi, kaksi tai kolme sitoutunutta happimolekyyliä. Kunkin välivaiheen muodostumista sitoutumattomasta hemoglobiinista voidaan kuvata näennäisen makroskooppisen assosiaatiovakion K i {\displaystyle K_{i}} avulla.

. Tuloksena oleva fraktionaalinen miehitys voidaan ilmaista seuraavasti: Y ¯ = 1 4 ⋅ K I + 2 K I I I 2 + 3 K I I I I 3 + 4 K I V 4 1 + K I + K I I 2 + K I I I 2 + K I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, mille tahansa proteiinille, jolla on n ligandin sitoutumiskohtaa:

Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n n 1 + K I + K I I 2 + …. + K n n {\displaystyle {\bar {Y}}={\frac {1}{n}}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

jossa n tarkoittaa sitoutumiskohtien lukumäärää ja jokainen K i {\displaystyle K_{i}}

on yhdistetty assosiaatiovakio, joka kuvaa i ligandimolekyylin sitoutumista.Yhdistämällä Adair-käsittely ja Hillin kuvaaja, päästään nykyaikaiseen kokeelliseen määritelmään kooperatiivisuudelle (Hill, 1985, Abeliovich, 2005). Tuloksena saadun Hillin kertoimen tai oikeammin Adairin yhtälöstä lasketun Hillin kuvaajan kaltevuuden voidaan osoittaa olevan sitoutumisluvun varianssin suhde sitoutumisluvun varianssiin vastaavassa ei-interagoivien sitoutumiskohtien järjestelmässä. Näin ollen Hillin kerroin määrittelee yhteistoiminnallisuuden yhden sitoutumiskohdan tilastollisena riippuvuutena muiden kohtien tilasta.

Klotzin yhtälöEdit

Työskennellessään kalsiumia sitovien proteiinien parissa Irving Klotz purki Adairin assosiaatiovakioita ottamalla huomioon välivaiheiden vaiheittaisen muodostumisen ja pyrki ilmaisemaan yhteistoiminnallisen sitoutumisen massan vaikutuksen lain säätelemien alkeisprosessien avulla. Hänen mukaansa K 1 {\displaystyle K_{1}}

on ensimmäisen ligandimolekyylin sitoutumista ohjaava assosiaatiovakio, K 2 {\displaystyle K_{2}}

toisen ligandimolekyylin sitoutumista ohjaava assosiaatiovakio (kun ensimmäinen on jo sitoutunut) jne. For Y ¯ {\displaystyle {\bar {Y}}}

saadaan: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {\displaystyle {\bar {Y}}={\frac {1}{n}}}{\frac {K_{1}+2K_{1}K_{2}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

On syytä huomata, että vakiot K 1 {\displaystyle K_{1}}}

, K 2 {\displaystyle K_{2}}

ja niin edelleen eivät liity yksittäisiin sitoutumiskohtiin. Ne kuvaavat pikemminkin sitä, kuinka monta sitoutumispaikkaa on varattu, kuin sitä, mitkä niistä ovat varattuja. Tämän muodon etuna on, että yhteistoiminnallisuus on helppo tunnistaa, kun tarkastellaan assosiaatiovakioita. Jos kaikki ligandin sitoutumispaikat ovat identtisiä ja niillä on mikroskooppinen assosiaatiovakio K {\displaystyle K}

, voitaisiin odottaa, että K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}}K,\ldots K_{n}={\frac {1}{n}}}K}

(eli K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}K}K}

) ilman yhteistoiminnallisuutta. Meillä on positiivinen yhteistoiminnallisuus, jos K i {\displaystyle K_{i}}

on näiden odotusarvojen yläpuolella i > 1 {\displaystyle i>1}

.

Klotzin yhtälöä (jota joskus kutsutaan myös Adair-Klotzin yhtälöksi) käytetään edelleen usein kokeellisessa kirjallisuudessa kuvaamaan ligandin sitoutumisen mittauksia peräkkäisinä näennäisinä sitoutumisvakioina.

Paulingin yhtälöMuokkaa

1900-luvun puolivälissä kiinnostus malleihin, jotka eivät kuvaisi sitoutumiskäyriä vain fenomenologisesti, vaan tarjoaisivat myös taustalla olevan biokemiallisen mekanismin, kasvoi. Linus Pauling tulkitsi Adairin esittämän yhtälön uudelleen olettaen, että hänen vakionsa olivat ligandin sitoutumisvakion ( K {\displaystyle K}

alla olevassa yhtälössä) ja yhteistoimintaproteiinin alayksiköiden välisestä vuorovaikutuksesta tulevan energian ( α {\displaystyle \alpha }

alla) yhdistelmä. Pauling itse asiassa johti useita yhtälöitä riippuen alayksiköiden välisen vuorovaikutuksen asteesta. Hemien lokalisaatiota koskevien väärien oletusten perusteella hän valitsi hemien hapen sitoutumista hemoglobiiniin kuvaavan väärän yhtälön olettaen, että alayksiköt olisivat järjestäytyneet neliöön. Alla olevassa yhtälössä esitetään yhtälö tetraedriselle rakenteelle, joka olisi tarkempi hemoglobiinin tapauksessa: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 2 + 4 α 3 K 3 3 + α 6 K 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alpha {}K^{2}^{2}+3\alpha {}^{3}K^{3}^{3}+\alpha {}^{6}K^{4}^{4}}{1+4K+6\alpha {}K^{2}^{2}+4\alpha {}^{3}K^{3}^{3}^{3}+\alpha {}^{6}K^{4}^{4}^{4}}}}

KNF-malliEdit

Perustuu tuloksiin, jotka osoittavat, että yhteistoimintaproteiinien rakenne muuttuu niiden sitoutuessa ligandiinsa, Daniel Koshland ja kollegat tarkensivat Paulingin kuvaaman mekanismin biokemiallista selitystä. Koshland-Némethy-Filmer (KNF) -mallissa (Koshland-Némethy-Filmer) oletetaan, että kukin alayksikkö voi olla kahdessa konformaatiossa: aktiivisessa tai inaktiivisessa. Ligandin sitoutuminen johonkin alayksikköön aiheuttaisi kyseisen alayksikön välittömän konformaatiomuutoksen inaktiivisesta aktiiviseen konformaatioon, mekanismi, jota kuvataan nimellä “indusoitu sovitus”. KNF-mallin mukaan yhteistoiminta syntyisi alayksiköiden välisistä vuorovaikutuksista, joiden voimakkuus vaihtelee alayksiköiden suhteellisten konformaatioiden mukaan. Tetraedriselle rakenteelle (he tarkastelivat myös lineaarisia ja neliömäisiä rakenteita) he ehdottivat seuraavaa kaavaa:

Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Jossa K X {\displaystyle K_{X}}

on X:n assosiaatiovakio, K t {\displaystyle K_{t}}

on B- ja A-tilojen suhde ilman ligandia (“siirtymä”), K A B {\displaystyle K_{AB}}

ja K B B {\displaystyle K_{BB}}

ovat vierekkäisten alayksikköparien suhteelliset stabiilisuudet suhteessa pariin, jossa molemmat alayksiköt ovat A-tilassa (Huomaa, että KNF-paperissa esitetään itse asiassa N s {\displaystyle N_{s}}

, varattujen paikkojen lukumäärää, joka on tässä 4 kertaa Y ¯ {\displaystyle {\bar {Y}}}

).

MWC-malliEdit

Monod-Wyman-Changeux-mallin reaktiokaavio kahdesta protomeeristä koostuvalle proteiinille. Protomeeri voi olla olemassa kahdessa tilassa, joilla kummallakin on erilainen affiniteetti ligandiin. L on tilojen suhde ligandin puuttuessa, c on affiniteettien suhde.

Energiakaavio kahdesta protomeeristä koostuvan proteiinin Monod-Wyman-Changeux-mallista. Ligandin suurempi affiniteetti R-tilaan tarkoittaa, että jälkimmäinen stabiloituu mieluummin sitoutumalla.

Monod-Wyman-Changeux (MWC) -malli koordinoituja allosterisia siirtymiä varten meni askeleen pidemmälle tutkimalla yhteistoiminnallisuutta termodynamiikan ja kolmiulotteisten konformaatioiden perusteella. Se muotoiltiin alun perin oligomeerisille proteiineille, joissa on symmetrisesti järjestettyjä, identtisiä alayksiköitä, joista jokaisella on yksi ligandin sitoutumiskohta. Tämän viitekehyksen mukaan allosteerisen proteiinin kaksi (tai useampi) keskenään muunneltavaa konformaatiotilaa vallitsee rinnakkain termisessä tasapainossa. Tilat, joita kutsutaan usein jännittyneiksi (T) ja rentoiksi (R), eroavat toisistaan affiniteetiltaan ligandimolekyyliä kohtaan. Näiden kahden tilan välistä suhdetta säädellään sitomalla ligandimolekyylejä, jotka stabiloivat suuremman affiniteetin omaavaa tilaa. Tärkeää on, että kaikki molekyylin alayksiköt vaihtavat tiloja samanaikaisesti, ilmiö tunnetaan nimellä “koordinoitu siirtyminen”.

Allosterinen isomerisaatiovakio L kuvaa tasapainoa molempien tilojen välillä, kun ligandimolekyyliä ei ole sidottu: L = {\displaystyle L={\frac {\left}{\left}}}

. Jos L on hyvin suuri, suurin osa proteiinista on T-tilassa ilman ligandia. Jos L on pieni (lähellä yhtä), R-tilassa on lähes yhtä paljon ihmisiä kuin T-tilassa. Ligandin T- ja R-tilojen dissosiaatiovakioiden suhdetta kuvaa vakio c: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Jos c = 1 {\displaystyle c=1}

, sekä R- että T-tiloilla on sama affiniteetti ligandiin eikä ligandi vaikuta isomerisaatioon. C:n arvo kertoo myös, kuinka paljon T- ja R-tilojen välinen tasapaino muuttuu ligandin sitoutuessa: mitä pienempi c on, sitä enemmän tasapaino siirtyy yhden sitoutumisen jälkeen kohti R-tilaa. Kun α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}

, osittainen miehitys kuvataan seuraavasti: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Allosteristen proteiinien sigmoidista Hillin kuvaajaa voidaan tällöin analysoida asteittaisena siirtymänä T-tilasta (matala affiniteetti) R-tilaan (korkea affiniteetti) saturaation kasvaessa. Hillin kuvaajan kaltevuus riippuu myös saturaatiosta, ja sen maksimiarvo on käännepisteessä. Kahden asymptootin ja y-akselin välisten leikkauspisteiden avulla voidaan määrittää molempien tilojen affiniteetit ligandille.

MWC-sitoutumisfunktion Hill plot punaisella, puhtaan T- ja R-tilan Hill plot vihreällä. Kun konformaatio siirtyy T:stä R:ään, niin myös sitoutumisfunktio muuttuu. X-akselin leikkauspisteistä saadaan näennäinen dissosiaatiovakio sekä R- ja T-tilojen mikroskooppiset dissosiaatiovakiot.

Proteiineissa konformaatiomuutos liittyy usein aktiivisuuteen tai aktiivisuuteen tiettyjä kohteita kohtaan. Tällainen aktiivisuus on usein se, mikä on fysiologisesti merkityksellistä tai mitä kokeellisesti mitataan. Konformaatiomuutoksen astetta kuvataan tilafunktiolla R ¯ {\displaystyle {\bar {R}}}

, joka tarkoittaa proteiinin osuutta, joka on läsnä R {\displaystyle R}

state. Kuten energiadiagrammi osoittaa, R ¯ {\displaystyle {\bar {R}}}

kasvaa, kun useampi ligandimolekyyli sitoutuu. Lauseke R ¯ {\displaystyle {\bar {R}}}

on: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}={\frac {(1+\alpha )^{n}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Keskeinen näkökohta MWC-mallissa on se, että käyrät Y ¯ {\displaystyle {\bar {Y}}}

ja R ¯ {\displaystyle {\bar {R}}}}

eivät osu yksiin, eli fraktionaalinen kyllästys ei ole suora konformaatiotilan (ja siten aktiivisuuden) indikaattori. Lisäksi sitoutumisen ja aktivoitumisen yhteistoiminnallisuuden laajuudet voivat olla hyvin erilaisia: ääritapauksen tarjoaa bakteerien lippulaivamoottori, jonka Hill-kerroin on 1,7 sitoutumiselle ja 10,3 aktivoitumiselle. Vasteen supralineaarisuutta kutsutaan joskus ultrasensitiivisyydeksi.

Jos allosterinen proteiini sitoutuu kohteeseen, jolla on myös korkeampi affiniteetti R-tilaan, niin kohteen sitoutuminen vakauttaa R-tilaa entisestään, mikä lisää ligandin affiniteettia. Jos taas kohde sitoutuu ensisijaisesti T-tilaan, niin kohteen sitoutumisella on negatiivinen vaikutus ligandin affiniteettiin. Tällaisia kohteita kutsutaan allosterisiksi modulaattoreiksi.

MWC-kehystä on laajennettu ja yleistetty sen syntymisen jälkeen. Siitä on ehdotettu muunnelmia esimerkiksi sellaisten proteiinien huomioon ottamiseksi, joilla on enemmän kuin kaksi tilaa, proteiinien, jotka sitoutuvat useisiin erityyppisiin ligandeihin tai useisiin erityyppisiin allosterisiin modulaattoreihin, ja proteiinien, joilla on ei-identtisiä alayksiköitä tai ligandin sitoutumiskohtia.