Le travail est défini comme l’énergie, que vous ajoutez à un objet en appliquant une force F sur une certaine distance r.

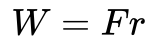
Cela peut signifier par exemple soulever un objet sur une distance r contre la gravité. L’énergie ajoutée est alors de l’énergie potentielle. Cependant, dans ce cas, je veux montrer comment le travail est lié à l’énergie cinétique.

Si vous appliquez une force à un objet, pour qu’il se déplace plus rapidement, vous augmentez son énergie cinétique.

Je vais montrer comment les deux sont liés en utilisant l’une des équations de mouvement que j’ai couvertes précédemment.

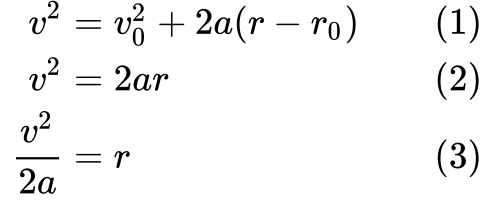
Nous commençons par la définition (1) puis nous la simplifions (2) en disant que la vitesse initiale v₀ et la distance initiale parcourue r₀ sont toutes deux nulles.

Enfin, nous réarrangeons (3)l’équation pour obtenir une façon d’exprimer r, afin de pouvoir la substituer dans W = Fr.

Nous voulons aussi nous débarrasser de l’accélération dans l’équation, car l’expression de l’énergie cinétique ne la contient pas. Réarrangeons la deuxième loi de Newton:

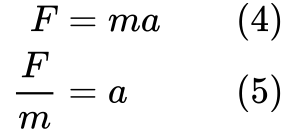
Maintenant nous avons les pièces pour dériver l’équation de l’énergie cinétique.

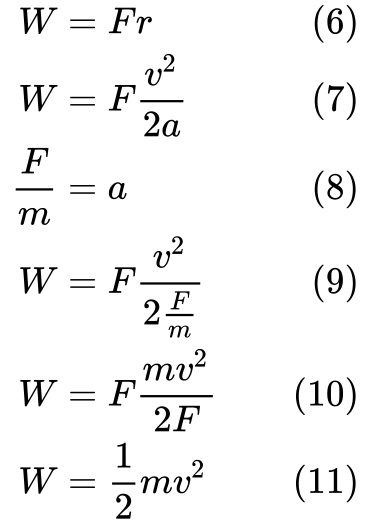
(7) substituer r avec l’équation (3). Ensuite, nous pouvons substituer a dans l’équation (9) avec la définition pour l’accélération dans l’équation (8).

Enfin (11) nous pouvons voir que le travail est égal à l’énergie cinétique.

En relisant ce post par hasard, j’ai remarqué que mon approche aurait pu être beaucoup plus simple.

Si nous commençons avec W = Fv²/2a et F = ma alors nous substituons F directement au lieu de a, et obtenons W = mav²/2a à la place. Ensuite, a est facilement éliminé et nous nous retrouvons avec W = mv²/2.