6.3 Belief Networks
Het begrip voorwaardelijke onafhankelijkheid kan worden gebruikt om een beknopte voorstelling te geven van vele domeinen. Het idee is dat, gegeven een willekeurige variabele X, er een kleine verzameling variabelen kan bestaan die de waarde van de variabele rechtstreeks beïnvloedt in die zin dat X voorwaardelijk onafhankelijk is van andere variabelen gegeven waarden voor de rechtstreeks beïnvloedende variabelen. De verzameling variabelen die plaatselijk van invloed zijn, wordt de Markov-deken genoemd. Deze lokaliteit wordt benut in een overtuigingsnetwerk. Een overtuigingsnetwerk is een gericht model van voorwaardelijke afhankelijkheid tussen een verzameling willekeurige variabelen. De precieze verklaring van voorwaardelijke onafhankelijkheid in een overtuigingsnetwerk houdt rekening met de directionaliteit.
Om een overtuigingsnetwerk te definiëren, begint men met een verzameling willekeurige variabelen die alle kenmerken van het model vertegenwoordigen. Stel dat deze variabelen {X1,…,Xn} zijn.Kies vervolgens een totale rangschikking van de variabelen, X1,…,Xn.
De kettingregel (Propositie 6.3) laat zien hoe een conjunctie kan worden ontbonden in conditionele waarschijnlijkheden:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Of, in termen van willekeurige variabelen en kansverdelingen,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definieer de ouders van de toevalsvariabele Xi, geschreven alsouders(Xi), als de kleinste verzameling voorgangers van Xi in de totale ordening, zodat de andere voorgangers van Xi voorwaardelijk onafhankelijk zijn van Xi gegevenouders(Xi). Dat wil zeggen, parents(Xi) ⊆{X1,…,Xi-1} zo dat
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Als er meer dan één minimale verzameling bestaat, kan elke minimale verzameling als ouders worden gekozen. Er kan alleen meer dan één minimale verzameling zijn als sommige van de voorgangers deterministische functies van andere zijn.
We kunnen de kettingregel en de definitie van ouders samenvoegen, wat
P(X1, X2,—, Xn) = ∏i=1n P(Xi|parents(Xi)) oplevert.
De kans over alle variabelen, P(X1, X2,—,Xn), wordt de gezamenlijke kansverdeling genoemd. Een overtuigingsnetwerk definieert een factorisatie van de gezamenlijke kansverdeling, waarbij de voorwaardelijke kansen factoren vormen die met elkaar worden vermenigvuldigd.
Een overtuigingsnetwerk, ook wel Bayesiannetwerk genoemd, is een acyclisch gerichte grafiek (DAG), waarvan de knopen willekeurige variabelen zijn. Er is een boog van elk element vanparents(Xi) naar Xi.Geassocieerd met het overtuigingsnetwerk is een verzameling conditionele waarschijnlijkheidsdistributies – de conditionele waarschijnlijkheid van elke variabele gegeven zijn ouders (die de voorafgaande waarschijnlijkheden van dievariabelen zonder ouders omvat).
Dus bestaat een overtuigingsnetwerk uit
- een DAG, waarin elke knoop gelabeld is met een willekeurige variabele;
- een domein voor elke willekeurige variabele; en
- een verzameling conditionele waarschijnlijkheidsverdelingen die P(X|ouders(X)) geven voor elke variabele X.
Een overtuigingsnetwerk is acyclisch door constructie. De manier waarop de kettingregel de conjunctie samenstelt, geeft de volgorde aan. Een variabele kan alleen voorgangers als ouders hebben.Verschillende decomposities kunnen resulteren in verschillende overtuigingsnetwerken.
Suppose we gebruiken de volgende variabelen, die alle Booleaans zijn, in de volgende volgorde:
- Knoeien is waar als er met het alarm is geknoeid.
- Brand is waar als er brand is.
- Alarm is waar als het alarm afgaat.
- Rook is waar als er rook is.
- Verlaten is waar als er veel mensen tegelijk het gebouw verlaten.
- Melding is waar als er door iemand een melding is gedaan van mensen die het gebouw verlaten. Report is false als er geen melding van vertrek is.
De variabele Report geeft de sensormelding aan dat er mensen vertrekken. Deze informatie is onbetrouwbaar omdat de persoon die zo’n melding geeft een practical joke kan uithalen, of omdat niemand die zo’n melding had kunnen geven, heeft opgelet. Deze variabele wordt geïntroduceerd om conditionering op onbetrouwbare sensor data mogelijk te maken. De agent weet wat de sensor rapporteert, maar hij heeft alleen onbetrouwbaar bewijs over mensen die het gebouw verlaten.Als onderdeel van het domein, veronderstel de volgende voorwaardelijke onafhankelijkheden:
- Brand is voorwaardelijk onafhankelijk van sabotage (gegeven geen andere informatie).
- Alarm is afhankelijk van zowel Brand als sabotage. Dat wil zeggen, we maken geen onafhankelijkheids aannames over hoe Alarm afhangt van zijn voorgangers gegeven deze variabele volgorde.
- Rook hangt alleen af van Vuur en is voorwaardelijk onafhankelijk van Sabotage en Alarm gegeven of er een Vuur is.
- Verlaten hangt alleen af van Alarm en niet direct van Vuur of Sabotage of Rook. Dat wil zeggen, Verlaten is voorwaardelijk onafhankelijk van de andere variabelen gegeven Alarm.
- Melding hangt alleen direct af van Verlaten.
Het overtuigingsnetwerk van figuur 6.1 drukt deze afhankelijkheden uit.
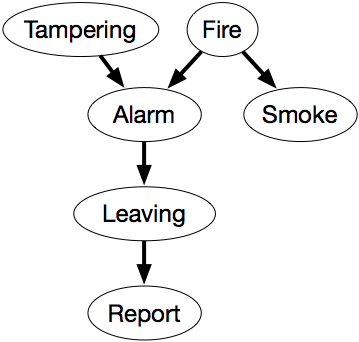
Dit netwerk vertegenwoordigt de factorisatie
P(Knoeien,Brand,Alarm,Rook,Verlaten,Melding) = P(Knoeien) ×P(Brand) ×P(Alarm|Knoeien,Brand) ×P(Rook|Vuur) ×P(Verlaten|Alarm) ×P(Melding|Verlaten).
We moeten ook het domein van elke variabele definiëren. Veronderstel dat de variabelen Booleaans zijn, dat wil zeggen dat ze het domein {waar,onwaar} hebben. We gebruiken de kleine letters van de variabele om de ware waarde weer te geven en gebruiken negatie voor de valse waarde. Dus, bijvoorbeeld, Tamponeren=waar wordt geschreven als Tamponeren, en Tamponeren=vals wordt geschreven als ¬tamponeren.
De volgende voorbeelden gaan uit van de volgende voorwaardelijke kansen:
P(brand) = 0.01
P(alarm | brand ∧sabotage) = 0.5
P(alarm | brand ∧¬tampering) = 0.99
P(alarm | ¬vuur ∧tampering) = 0.85
P(alarm | ¬vuur ∧¬tampering) = 0.0001
P(rook | vuur ) = 0.9
P(rook | ¬brand ) = 0,01
P(weggaan | alarm) = 0,88
P(weggaan | ¬alarm ) = 0,001
P(melding | weggaan ) = 0,75
P(melding | ¬weggaan ) = 0.01
- Voor elke draad wi is er een willekeurige variabele, Wi, in het domein {live,dead}, die aangeeft of er stroom is in draad wi. Wi=levend betekent dat draadwi stroom heeft. Wi=dood betekent dat er geen stroom is in draad wi.
- Outside_power met domein {live,dead} geeft aan of er stroom in het gebouw komt.
- Voor elke schakelaar si geeft de variabele Si_pos de positie vansi aan. Deze heeft het domein {up,down}.
- Voor elke schakelaar si, geeft de variabele Si_st de toestand van schakelaar si aan. Ithas domein {ok,upside_down,short,intermittent,broken}. Si_st=ok betekent dat de schakelaar si normaal werkt. Si_st=upside_down betekent dat schakelaar si ondersteboven is geïnstalleerd. Si_st=kort betekent dat schakelaar si is ingekort en als een draad werkt. Si_st=gebroken betekent dat schakelaar si kapot is en geen stroom doorlaat.
- Voor elke stroomonderbrekerercbi heeft variabele Cbi_st het domein {on,off}. Cbi_st=on betekent dat er stroom door cbi kan stromen en Cbi_st=off betekent dat er geen stroom door cbi kan stromen.
- Voor elk lampje li geeft de variabele Li_st met domein {ok,intermittent,broken} de toestand van het lampje aan. Li_st=ok betekent dat licht li brandt als er stroom op staat, Li_st=intermitterend betekent dat licht li met tussenpozen brandt als er stroom op staat, en Li_st=gebroken betekent dat licht li niet werkt.
Laten we een ordening kiezen waarbij de oorzaken van een variabele vóór de variabele in de ordening staan. Bijvoorbeeld, de variabele of een lampje brandt komt na de variabelen of het lampje werkt en of er stroom in het lampje komt.
Of lampje l1 brandt hangt er alleen van af of er stroom in draad w0 zit en of lampje l1 goed werkt. Andere variabelen, zoals de stand van schakelaar s1, of lampje l2 brandt, of wie de koningin van Canada is, doen niet ter zake. De ouders van L1_lit zijn dus W0 en L1_st.
Overweeg variabele W0, die weergeeft of er stroom in draad w0 zit. Als we wisten of er stroom was in draden w1 en w2, en we wisten de stand van schakelaar s2 en of de schakelaar goed werkte, zou de waarde van de andere variabelen (behalve L1_lit) geen invloed hebben op ons geloof in de vraag of er stroom is in draad w0. De ouders van W0 zouden dus S2_Pos, S2_st,W1, en W2 moeten zijn.
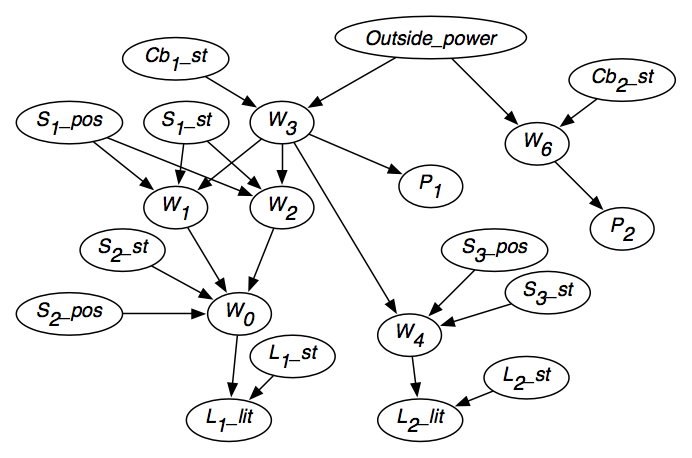
Figuur 6.2 toont het resulterende overtuigingsnetwerk nadat de afhankelijkheid van elke variabele in beschouwing is genomen.Het overtuigingsnetwerk bevat ook de domeinen van de variabelen, zoals gegeven in de figuur, en de voorwaardelijke waarschijnlijkheden van elke variabele gegeven zijn ouders.
Voor de variabele W1 moeten de volgende voorwaardelijke waarschijnlijkheden worden gespecificeerd:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=levend|S1_pos=omlaag ∧S1_st=omlaag ∧W3=dood).
Er zijn twee waarden voor S1_pos, vijf waarden voor S1_ok, en twee waarden voor W3, dus zijn er 2×5 ×2 = 20 verschillende gevallen waarin een waarde voor W1=levend moet worden gespecificeerd. Wat de waarschijnlijkheidstheorie betreft, kan de waarschijnlijkheid voor W1=levend voor deze 20 gevallen willekeurig worden toegekend. Kennis van het domein beperkt natuurlijk welke waarden zinvol zijn. De waarden voor W1=dood kunnen worden berekend uit de waarden voor W1=leven voor elk van deze gevallen.
Omdat de variabele S1_st geen ouders heeft, heeft zij een voorafgaande verdeling nodig, die kan worden gespecificeerd als de waarschijnlijkheden voor alle waarden op één na; de resterende waarde kan worden afgeleid uit de beperking dat alle waarschijnlijkheden bij elkaar opgeteld gelijk zijn aan 1. Dus, om de verdeling van S1_st te specificeren, moeten vier van de volgende vijf waarschijnlijkheden worden gespecificeerd:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Een overtuigingsnetwerk is een grafische voorstelling van voorwaardelijke onafhankelijkheid. De onafhankelijkheid stelt ons in staat directe effecten binnen de grafiek weer te geven en schrijft voor welke waarschijnlijkheden moeten worden gespecificeerd. Arbitraireposterior waarschijnlijkheden kunnen uit het netwerk worden afgeleid.
De onafhankelijkheidsaanname die in een overtuigingsnetwerk is ingebed, is als volgt:Elke willekeurige variabele is voorwaardelijk onafhankelijk van zijn niet-afstammelingen, gegeven zijn ouders. Dat wil zeggen, als X een willekeurige variabele is met ouders Y1,…, Yn, zijn alle willekeurige variabelen die geen afstammelingen zijn vanX voorwaardelijk onafhankelijk van X gegeven Y1 ,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
als R geen afstammeling is van X. Voor deze definitie nemen we X op als een afstammeling van zichzelf. Het rechterlid van deze vergelijking is de vorm van de waarschijnlijkheden die worden gespecificeerd als onderdeel van het overtuigingsnetwerk.R mag betrekking hebben op voorouders van X en andere knooppunten, zolang ze maar geen afstammelingen zijn van X. De onafhankelijkheidsveronderstelling stelt dat alle invloed van niet-afstammende variabelen wordt opgevangen door de waarde van de ouders van X te kennen.
Maakelijk verwijzen we naar de gelabelde DAG als een overtuigingsnetwerk. Wanneer dit wordt gedaan, is het belangrijk om te onthouden dat een domein voor elke variabele en een set conditionele kansverdelingen ook deel uitmaken van het netwerk.
Het aantal kansen dat voor elkevariabele moet worden gespecificeerd, is exponentieel met het aantal ouders van de variabele.De onafhankelijkheidsaanname is nuttig voor zover het aantalvariabelen dat direct van invloed is op een andere variabele, klein is. U moet de variabelen zo rangschikken dat de knooppunten zo weinig mogelijk ouders hebben.
Overtuigingsnetwerken en Causaliteit
Veronderstellingsnetwerken worden vaak causale netwerken genoemd en er wordt beweerd dat ze een goede voorstelling van causaliteit zijn.Herinner u dat een causaal model het resultaat van interventies voorspelt.Stel dat u een causaal model van een domein in gedachten hebt, waarbij het domein gespecificeerd is in termen van een verzameling willekeurige variabelen. Voor elk paar willekeurige variabelen X1en X2, als er een direct oorzakelijk verband bestaat van X1 naar X2 (d.w.z., ingrijpen om X1 te veranderen in een bepaalde context van andere variabelen beïnvloedt X2 en dit kan niet worden gemodelleerd door een of andere interveniërende variabele), voeg dan een boog toe vanX1 naar X2. Je zou verwachten dat het causale model gehoorzaamt aan de onafhankelijkheidsaanname van het overtuigingsnetwerk. Je zou dus verwachten dat alle conclusies van het overtuigingsnetwerk geldig zijn.
Je zou ook verwachten dat zo’n grafiek acyclisch is; je wilt niet dat iets uiteindelijk zichzelf veroorzaakt. Deze aanname is redelijk als je bedenkt dat de willekeurige variabelen bepaalde gebeurtenissen vertegenwoordigen in plaats van soorten gebeurtenissen. Neem bijvoorbeeld een causale keten waarin “gestresst zijn” ervoor zorgt dat u “inefficiënt werkt”, wat er op zijn beurt weer toe leidt dat u “gestresst bent”. Om de schijnbare cyclus te doorbreken, kunnen we “gestresst zijn” in verschillende stadia voorstellen als verschillende willekeurige variabelen die verwijzen naar verschillende tijden. Gestresst zijn in het verleden zorgt ervoor dat u op dit moment niet goed werkt, waardoor u in de toekomst gestresst zult zijn. De variabelen moeten voldoen aan het helderheidsbeginsel en een welomschreven betekenis hebben. De variabelen moeten niet worden gezien als gebeurtenistypen.
Het overtuigingsnetwerk zelf heeft niets te zeggen over causaliteit, en het kan niet-causale onafhankelijkheid representeren, maar het lijkt bijzonder geschikt als er causaliteit in een domein is. Door het toevoegen van bogen die lokale causaliteit weergeven, ontstaat een klein overtuigingsnetwerk. Het overtuigingsnetwerk vanFiguur 6.2 laat zien hoe dit kan worden gedaan voor een eenvoudig domein.
Acausaal netwerk modelleert interventies. Als iemand een variabele kunstmatig zou dwingen een bepaalde waarde te hebben, zouden de nakomelingen van die variabele – maar geen andere knooppunten – worden beïnvloed. Tenslotte kun je zien hoe causaliteit in overtuigingsnetwerken samenhangt met causaal en bewijskrachtig redeneren, zoals besproken in Paragraaf 5.7. Een causaal overtuigingsnetwerk kan worden gezien als een weg van axiomatiseren in een causale richting. Redeneren in overtuigingsnetwerken komt neer op het afleiden van oorzaken en vervolgens het doen van voorspellingen op grond daarvan. Er bestaat een directe koppeling tussen de op logica gebaseerde abductieve zienswijze die in Paragraaf 5.7 is besproken en overtuigingsnetwerken: Overtuigingsnetwerken kunnen worden gemodelleerd als logische programma’s met waarschijnlijkheden over mogelijke hypothesen. Dit wordt beschreven in Paragraaf 14.3.
Let op de restrictie “elke willekeurige variabele is voorwaardelijk onafhankelijk van zijn niet-afstammelingen gegeven zijn ouders” in de definitie van de onafhankelijkheid die in een overtuigingsnetwerk is gecodeerd. AlsR een descendant van variabele X bevat, is de onafhankelijkheidsaanname niet direct van toepassing.
De variabele S1_pos heeft geen ouders. De in het overtuigingsnetwerk ingebedde onafhankelijkheid specificeert dus dat P(S1_pos=up|A) =P(S1_pos=up) voor elke A die geen nakomeling vanS1_pos bevat. Als A een afstammeling van S1_pos=up bevat – bijvoorbeeld, als A S2_pos=up∧L1_lit=true is – kan de onafhankelijkheidsassumptie niet direct worden toegepast.
Dit netwerk kan op een aantal manieren worden gebruikt:
- Door te conditioneren op de kennis dat de schakelaars en stroomonderbrekers in orde zijn, en op de waarden van de buitenstroom en de stand van de schakelaars, kan dit netwerk simuleren hoe de verlichting zou moeten werken.
- Gegeven waarden van de externe stroom en de stand van de schakelaars, kan het netwerk de waarschijnlijkheid van elk resultaat afleiden – bijvoorbeeld, hoe groot de kans is dat l1 brandt.
- Gegeven waarden voor de schakelaars en of de lichten branden, kan de posterior waarschijnlijkheid dat elke schakelaar of stroomonderbreker in een bepaalde toestand is, worden afgeleid.
- Gegeven sommige waarnemingen, kan het netwerk worden gebruikt om terug te redeneren om de meest waarschijnlijke positie van schakelaars te bepalen.
- Gegeven enkele schakelaarposities, enkele uitgangen, en enkele tussenliggende waarden, kan het netwerk worden gebruikt om de waarschijnlijkheid van enige andere variabele in het netwerk te bepalen.
Een overtuigingsnetwerk specificeert een gezamenlijke waarschijnlijkheidsverdeling waaruit willekeurige voorwaardelijke waarschijnlijkheden kunnen worden afgeleid. Een netwerk kan worden opgevraagd door te vragen naar de conditionele waarschijnlijkheid van variabelen, geconditioneerd op de waarden van andere variabelen. Dit wordt meestal gedaan door waarnemingen op te geven van enkele variabelen en een andere variabele op te vragen.
P(brand) = 0.01
P(melding ) = 0.028
P(rook) = 0.0189
Observeren van het rapport geeft het volgende:
P(fire |report)= 0,2305
P(smoke |report) = 0,215
Zoals verwacht, neemt de kans op zowel sabotage als brand toe door het rapport. Omdat brand is toegenomen, is de kans op rook ook toegenomen.
Stel nu eens dat rook werd waargenomen:
P(brand|rook) = 0,476
P(melding|rook) = 0,320
Merk op dat de kans op sabotage niet wordt beïnvloed door de waarneming van rook; de kansen op melding en brand worden echter wel verhoogd.
Stel dat zowel melding als rook werden waargenomen:
P(brand | melding ∧rook) = 0,964
Door beide waar te nemen wordt brand nog waarschijnlijker. Echter, in de context van de melding, maakt de aanwezigheid van rook sabotage minder waarschijnlijk. Dit komt doordat de melding wordt verklaard door vuur, dat nu waarschijnlijker is.
Stel dat wel melding, maar geen rook werd waargenomen:
P(fire|report ∧¬smoke) = 0,0294
In de context van de melding wordt brand veel minder waarschijnlijk en neemt de waarschijnlijkheid van sabotage toe om de melding te verklaren.
Dit voorbeeld illustreert hoe de onafhankelijkheidsaanname van het overtuigingsnetwerk commonsense-conclusies oplevert en laat ook zien hoe het wegverklaren een gevolg is van de onafhankelijkheidsaanname van een overtuigingsnetwerk.
- 6.3.1 Overtuigingsnetwerken construeren