In het begin is het meestal nodig om een idee te krijgen van het pV-diagram van de cyclus. Daartoe zullen wij de krommen van de isochorische en adiabatische processen traceren. De grafiek van de Otto cyclus is bij benadering weergegeven in de volgende figuur.
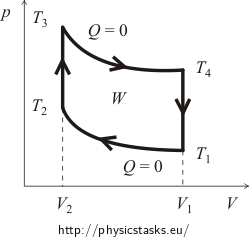
Het rendement η van de cyclus wordt gedefinieerd als
waarbij W de arbeid is die door het gas gedurende één cyclus wordt verricht minus de arbeid die door de externe krachten wordt verricht (in het diagram wordt dit weergegeven door de oppervlakte van het gebied dat wordt gedefinieerd door de lijnen van de cyclus!) en Qsup de warmte is die tijdens de cyclus aan het systeem wordt toegevoerd.
De arbeid W kan worden berekend met behulp van het verband tussen de druk en het volume tijdens een adiabatische uitzetting en compressie (de arbeid die wordt verricht tijdens een isochorisch proces is uiteraard nul). In deze opgave zal het echter beter zijn gebruik te maken van het feit dat de totale verandering van de inwendige energie per cyclus gelijk moet zijn aan nul (we komen terug in dezelfde toestand als bij het begin, dus de temperatuur en dus de inwendige energie blijven gelijk!). Volgens de eerste thermodynamische wet kan de door het gas verrichte arbeid worden uitgedrukt als het verschil tussen de geleverde warmte Qsup en de afgegeven warmte Qrel. De formule voor het rendement van de cyclus is dus van de vorm
Eerst zullen we de toegevoerde warmte Qsup berekenen. Het is duidelijk dat er tijdens het adiabatische proces geen warmte-uitwisseling plaatsvindt en dat tijdens de isochorische afkoeling de warmte wordt afgegeven. Dit betekent dat de warmte alleen wordt toegevoerd tijdens de isochorische verwarming van de temperatuur T2 tot de temperatuur T3. De hoeveelheid van deze warmte kan als volgt worden uitgedrukt in de variabelen van de hoeveelheid stof n van het gas en zijn molaire warmtecapaciteit CV:
Wij zullen de hoeveelheid van de afgegeven warmte Qrel op ongeveer dezelfde wijze uitdrukken. We weten al dat de warmte alleen vrijkomt tijdens de isochorische afkoeling van de temperatuur T4 terug naar de begintemperatuur T1. Het is waar dat:
\
Nu we deze formules substitueren in de formule van het rendement van de cyclus, krijgen we onmiddellijk:
\
Nu moeten we de temperatuurverschillen uitdrukken met behulp van de gegeven compressieverhouding
\
en de Poissonverhouding κ.
Daartoe gebruiken we de vergelijking voor een ideaal gas dat een adiabatisch proces ondergaat (de wet van Poisson) pVκ = C = konst.., waarbij C een constante is. Nu berekenen we de druk uit de toestandsvergelijking van een ideaal gas
die we substitueren in de wet van Poisson. Nu schuiven we de constanten (C en K) naar één kant \
Nu passen we deze wet van Poisson toe voor beide adiabatische processen. Voor de adiabatische uitzetting krijgen we de relatie
\
En voor de adiabatische compressie krijgen we
\
Nu trekken we de tweede vergelijking van de eerste af en ontbinden V1κ – 1 aan de ene kant en V2κ – 1 aan de andere kant. Zo krijgen we:
\
We zien dat we er daadwerkelijk in geslaagd zijn de temperatuurverschillen uit te drukken met behulp van de gegeven waarden. Als we dit verband in de formule voor het rendement invoeren, krijgen we de uiteindelijke vergelijking:
\