Aristoteles (Ἀριστοτέλης) 384-322 BCE was een Grieks filosoof en wetenschapper, geboren in de stad Stagira, in het klassieke Griekenland.

Op 17-jarige leeftijd werd hij lid van Plato’s Academie in Athene en bleef daar tot zijn zevenendertigste (ca. 347 v.Chr.)

Zijn geschriften bestrijken vele onderwerpen – waaronder natuurkunde, biologie, zoölogie, logica, ethiek, poëzie, theater, muziek, taalkunde en politiek. Ze vormen het eerste alomvattende systeem van de westerse filosofie.

• Opgenomen en aangepast van Aristoteles. (2016, 20 oktober). Wikipedia, The Free Encyclopedia.

Aristoteles stelde 3 bewegingswetten op, gebaseerd op waarnemingen (maar niet op experimenten)

* voorwerpen in de hemelen (de hemelse sfeer) bewegen in cirkelvormige beweging,zonder dat een externe kracht hen daartoe dwingt.voorwerpen op aarde (de aardse sfeer) bewegen in rechte lijnen, tenzij ze gedwongen worden in een cirkelvormige beweging te gaan.

Hoe zit het met duwen en trekken?

Natuurlijke versus onnatuurlijke beweging

Wat zou er dus gebeuren als een kanon een kanonskogel zou afvuren? Aristoteles veronderstelde dat deze in een rechte lijn zou bewegen (door de onnatuurlijke kracht), en daarna recht naar beneden zou vallen (door een andere, natuurlijke kracht.)

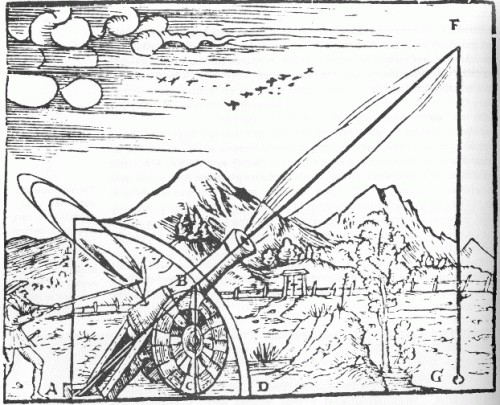
Voor Aristoteles is het zo dat zodra de “gewelddadige beweging” (van mensen) is uitgedoofd, de natuurlijke beweging het overneemt, en dan valt de kanonskogel naar zijn natuurlijke plaats, de aarde.

Hoewel, zoals Galielo in de jaren 1500 liet zien, Aristoteles’ opvatting helemaal niet juist is. Iedereen die naar een boogschutter kijkt die een pijl de lucht in schiet, en zorgvuldig observeert, zou zien dat dit niet gebeurt.

De verticale beweging neemt langzaam af, bereikt nul (op het hoogtepunt), en neemt dan toe in de tegenovergestelde (neerwaartse) richting.

Hemelse krachten vs aardse krachten

Aardse (aardse) voorwerpen werden verondersteld een aparte reeks bewegingswetten te hebben. Aardse voorwerpen zouden uit zichzelf altijd ophouden met bewegen.

*Voorwerpen bewegen van nature alleen in rechte lijnen. *Om voorwerpen een cirkelvormige beweging te laten maken, is een externe kracht nodig die ze in een cirkelvormig pad houdt.

Ook heeft Aristoteles nooit experimenten uitgevoerd, dus hij was zeer beperkt in wat hij kon waarnemen.In de middeleeuwen voerde Galileo (en anderen) gecontroleerde experimenten uit. De resultaten van deze experimenten werden geanalyseerd met wiskunde.

Galileo leerde kritische denkvaardigheden van zijn vader, Vincenzo

a. Als de bal naar beneden rolt, beweegt hij met de zwaartekracht van de aarde mee, en neemt zijn snelheid toe.

c. Als de bal op een vlakke ondergrond rolt, beweegt hij niet met of tegen de zwaartekracht in.

b. Als de hoek van de opwaartse helling kleiner wordt, rolt de bal een grotere afstand voordat hij zijn aanvankelijke hoogte heeft bereikt.

Galileo’s conclusie werd ondersteund door een andere redenering.

Inclined Plane – Galileo’s Battle for the Heavens PBS NOVA

Rolling balls, cylinders and tubes down inclined plane: Traagheidsmoment

Er is iets speciaals: De brachistochrone – kromme van de snelste afdaling. En de tautochrone – de kromme waarbij de tijd die een voorwerp dat zonder wrijving in uniforme zwaartekracht naar zijn laagste punt glijdt, nodig heeft, onafhankelijk is van zijn beginpunt.

De bewegingswetten van Aristoteles.

Uittreksel uit een lezing van professor Michael Fowler, U. Va. Physics, 9/3/2008

http://galileoandeinstein.physics.virginia.edu/lectures/aristot2.html

Wat Aristoteles in die jaren in Athene bereikte, was het begin van een school van georganiseerd wetenschappelijk onderzoek op een schaal die alles wat daarvoor was geweest, ver overtrof. Hij definieerde eerst duidelijk wat wetenschappelijke kennis was, en waarom die gezocht moest worden. Met andere woorden, hij vond eigenhandig de wetenschap uit als de collectieve, georganiseerde onderneming die het vandaag is. Plato’s Academie had het equivalent van een universitaire afdeling wiskunde, Aristoteles had de eerste wetenschappelijke afdeling, werkelijk uitstekend in biologie, maar, zoals we zullen zien, een beetje zwak in natuurkunde.

Na Aristoteles was er gedurende meer dan 2000 jaar geen vergelijkbare professionele wetenschappelijke onderneming, en zijn werk was van zo’n kwaliteit dat het door iedereen werd aanvaard, en 2000 jaar later al lang deel uitmaakte van de officiële orthodoxie van de Christelijke Kerk. Dit was ongelukkig, want toen Galilei enkele beweringen over de eenvoudige natuurkunde in twijfel trok, kwam hij al snel in ernstige moeilijkheden met de Kerk.
Aristoteles’ methode van onderzoek:

definitie van het onderwerp

beschouwing van de moeilijkheden, door het doornemen van de algemeen aanvaarde opvattingen over het onderwerp, en suggesties van eerdere schrijvers

presentatie van zijn eigen argumenten en oplossingen

Dit is het patroon dat moderne onderzoekspapers volgen, Aristoteles legde de standaard professionele benadering van wetenschappelijk onderzoek vast.

Aristoteles weerlegde vaak een tegenargument door aan te tonen dat het tot een absurde conclusie leidde, dit wordt reductio ad absurdum (iets tot absurditeit reduceren) genoemd. Zoals we later zullen zien, gebruikte Galileo precies dit soort argumenten tegen Aristoteles zelf, tot grote ergernis van Aristotelici 2000 jaar na Aristoteles.

In tegenstelling tot Plato, die vond dat de enige wetenschap die de moeite waard was de beschouwing van abstracte vormen was, beoefende Aristoteles gedetailleerde observatie en dissectie van planten en dieren, om te proberen te begrijpen hoe elk paste in het grote schema van de natuur, en het belang van de verschillende organen van dieren.

Het is van essentieel belang te beseffen dat de wereld die Aristoteles in het dagelijks leven om zich heen zag, inderdaad heel anders was dan die wij vandaag de dag zien. Ieder modern kind heeft vanaf zijn geboorte auto’s en vliegtuigen zien bewegen, en komt er al gauw achter dat deze dingen niet leven, zoals mensen en dieren. Daarentegen waren de meeste bewegingen in het Griekenland van de vierde eeuw mensen, dieren en vogels, die allemaal zeer levend waren. Deze beweging had allemaal een doel, het dier bewoog zich om een of andere reden naar een plaats waar het liever zou zijn, dus werd de beweging gestuurd door de wil van het dier.

Voor Aristoteles voldeed deze beweging dus aan de “natuur” van het dier, net zoals zijn natuurlijke groei voldeed aan de natuur van het dier.

Om de beweging van dingen die duidelijk niet leven, zoals een steen die uit de hand valt, te verklaren, breidde Aristoteles het concept van de “natuur” van iets uit tot levenloze materie. Hij stelde voor de beweging van zulke levenloze voorwerpen te begrijpen door te stellen dat elementen de neiging hebben hun natuurlijke plaats in de orde der dingen te zoeken:

Zo beweegt de aarde het sterkst naar beneden,
water stroomt ook naar beneden, maar niet zo sterk, want een steen valt door water heen.
Lucht daarentegen beweegt zich omhoog (bellen in water),
en vuur gaat het sterkst omhoog van alle, omdat het door de lucht omhoog schiet.

Deze algemene theorie over hoe elementen bewegen moet natuurlijk worden uitgewerkt, wanneer ze wordt toegepast op echte materialen, die mengsels van elementen zijn. Hij zou concluderen dat hout zowel aarde als lucht in zich heeft, omdat het niet in water zinkt.

Natuurlijke beweging en gewelddadige beweging

Dingen bewegen ook omdat ze geduwd worden. De natuurlijke neiging van een steen, als hij alleen en zonder steun wordt gelaten, is om te vallen, maar wij kunnen hem optillen, of zelfs door de lucht gooien.

Aristoteles noemde een dergelijke gedwongen beweging “gewelddadige” beweging in tegenstelling tot natuurlijke beweging.

De term “gewelddadig” betekent alleen dat er een of andere externe kracht op wordt uitgeoefend.

Aristoteles was de eerste die kwantitatief nadacht over de snelheden die bij deze bewegingen betrokken waren. Hij deed twee kwantitatieve beweringen over hoe dingen vallen (natuurlijke beweging):

Zwaardere dingen vallen sneller, waarbij de snelheid evenredig is met het gewicht.

De valsnelheid van een gegeven voorwerp hangt omgekeerd evenredig af van de dichtheid van het medium waardoor het valt.

Dus zal hetzelfde lichaam bijvoorbeeld twee keer zo snel vallen door een medium met de helft van de dichtheid.

Merk op dat deze regels een zekere elegantie bezitten, een aantrekkelijke kwantitatieve eenvoud. En, als je een steen en een stuk papier laat vallen, is het duidelijk dat het zwaardere ding sneller valt, en een steen die door water valt wordt zeker afgeremd door het water, dus de regels lijken op het eerste gezicht aannemelijk.

Het verrassende is, dat Aristoteles, gezien zijn nauwgezette waarnemingen van zoveel dingen, deze regels niet serieus heeft onderzocht.

Het zou niet lang geduurd hebben om uit te vinden of bijvoorbeeld een halve baksteen met de helft van de snelheid van een hele baksteen viel. Dit was duidelijk niet iets wat hij belangrijk vond.

Uit de tweede bewering hierboven concludeerde hij dat een vacuüm niet kan bestaan, want als dat wel zo was, omdat het een dichtheid van nul heeft, zouden alle lichamen er met oneindige snelheid doorheen vallen, wat duidelijk onzin is.

Voor gewelddadige beweging stelde Aristoteles dat de snelheid van het bewegende voorwerp recht evenredig was met de uitgeoefende kracht.

Dit betekent allereerst dat als je stopt met duwen, het voorwerp stopt met bewegen.

Dit klinkt zeker als een redelijke regel voor bijvoorbeeld
het duwen van een doos boeken over een tapijt, of een os die een ploeg door een akker sleept.

(Dit intuïtief aantrekkelijke beeld houdt echter geen rekening met
de grote wrijvingskracht tussen de doos en het tapijt.
Als je de doos op een slee zou zetten en over het ijs zou duwen,
zou de doos niet stoppen als je stopt met duwen.
Eeuwen later realiseerde Galileo zich het belang van wrijving in deze situaties.)

Leerstandaarden

2016 Massachusetts Science and Technology/Engineering Curriculum Framework
HS-PS2-1. Gegevens analyseren om de bewering te staven dat de tweede bewegingswet van Newton een
wiskundig model is dat de verandering in beweging (de versnelling) van objecten beschrijft wanneer
er op wordt ingewerkt door een netto kracht.

HS-PS2-10(MA). Gebruik vrije-lichaamskrachtendiagrammen, algebraïsche uitdrukkingen en de bewegingswetten van Newton om veranderingen in snelheid en versnelling te voorspellen voor een object dat in één dimensie beweegt in verschillende situaties

Massachusetts History and Social Science Curriculum Framework

De wortels van de westerse beschaving: Het oude Griekenland, C. 800-300 BCE.
7.34 Beschrijf de doelen en functies van de ontwikkeling van Griekse instellingen zoals het lyceum, het gymnasium, en de Bibliotheek van Alexandrië, en identificeer de belangrijkste prestaties van de oude Grieken.

WHI.33 Vat samen hoe de wetenschappelijke revolutie en de wetenschappelijke methode tot nieuwe theorieën over het heelal hebben geleid en beschrijf de prestaties van de leidende figuren van de wetenschappelijke revolutie, waaronder Bacon, Copernicus, Descartes, Galileo, Kepler, en Newton.

EEN KADER VOOR WETENSCHAPPELIJK ONDERWIJS VOOR K-12: Praktijken, overkoepelende concepten en kernideeën
PS2.A: KRACHTEN EN BEWEGING
Hoe kan men de voortdurende beweging, veranderingen in beweging of stabiliteit van een voorwerp voorspellen?

Interacties van een voorwerp met een ander voorwerp kunnen worden verklaard en voorspeld met behulp van het concept van krachten, die een verandering in de beweging van een of beide op elkaar inwerkende voorwerpen kunnen veroorzaken… Op macroschaal wordt de beweging van een voorwerp onderhevig aan krachten beheerst door de tweede bewegingswet van Newton… Inzicht in de krachten tussen voorwerpen is belangrijk om te beschrijven hoe hun bewegingen veranderen, en om de stabiliteit of instabiliteit van systemen op elke schaal te voorspellen.