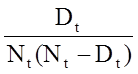Er zijn verschillende manieren om een overlevingsfunctie of een overlevingscurve te schatten. Er zijn een aantal populaire parametrische methoden die worden gebruikt om overlevingsgegevens te modelleren, en zij verschillen in termen van de veronderstellingen die worden gemaakt over de verdeling van overlevingstijden in de populatie. Enkele populaire verdelingen zijn de exponentiële, Weibull-, Gompertz- en lognormale verdelingen.2 Misschien is de exponentiële verdeling wel de populairste, die ervan uitgaat dat de waarschijnlijkheid dat een deelnemer de gebeurtenis van belang ondergaat, onafhankelijk is van hoe lang die persoon gebeurtenisvrij is geweest. Andere verdelingen maken verschillende veronderstellingen over de waarschijnlijkheid dat een individu een voorval ontwikkelt (d.w.z. dat deze kan toenemen, afnemen of veranderen in de loop van de tijd). Meer details over parametrische methoden voor overlevingsanalyse zijn te vinden in Hosmer en Lemeshow en Lee en Wang1,3.

Wij richten ons hier op twee niet-parametrische methoden, die geen veronderstellingen maken over hoe de waarschijnlijkheid dat een persoon een voorval ontwikkelt in de loop van de tijd verandert. Met niet-parametrische methoden schatten en plotten we de overlevingsverdeling of de overlevingscurve. Overlevingskrommen worden vaak uitgezet als stapfuncties, zoals in de onderstaande figuur. De tijd staat op de X-as en de overleving (percentage mensen dat risico loopt) staat op de Y-as. Merk op dat het percentage deelnemers dat overleeft niet altijd overeenkomt met het percentage dat in leven is (waarbij wordt verondersteld dat de uitkomst van belang de dood is). “Overleving” kan ook verwijzen naar het percentage dat vrij is van een andere gebeurtenis (bijv. percentage vrij van MI of hart- en vaatziekten), of het kan ook staan voor het percentage dat geen gezonde uitkomst heeft (bijv. remissie van kanker).

Survival Function

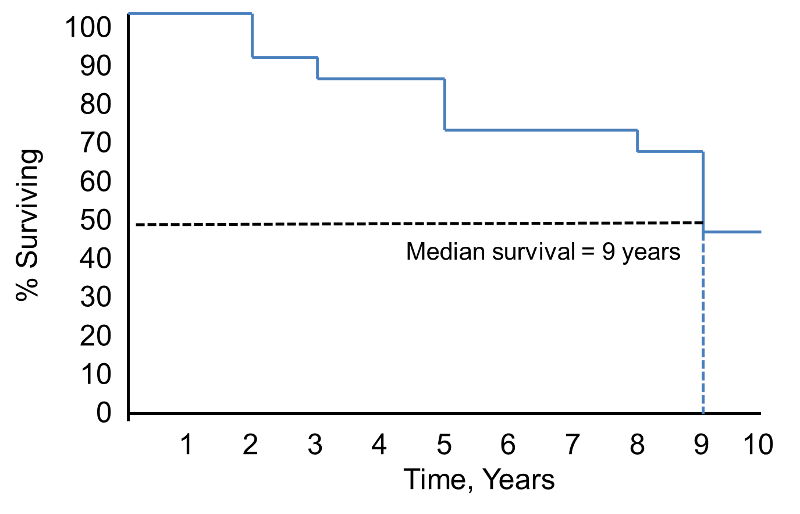
Merk op dat de overlevingskans gedurende 2 jaar 100% is en dan daalt tot 90%. De mediane overleving is 9 jaar (d.w.z. 50% van de populatie overleeft 9 jaar; zie stippellijnen).

Voorbeeld:

Beschouw een klein prospectief cohortonderzoek dat is opgezet om de tijd tot overlijden te bestuderen. Bij de studie zijn 20 deelnemers van 65 jaar en ouder betrokken; zij worden in een periode van 5 jaar ingeschreven en maximaal 24 jaar gevolgd totdat zij overlijden, de studie wordt beëindigd, of zij uit de studie stappen (lost to follow-up). De gegevens zijn hieronder weergegeven. In de studie zijn er 6 sterfgevallen en 3 deelnemers met volledige follow-up (d.w.z. 24 jaar). De overige 11 hebben minder dan 24 jaar follow-up als gevolg van te late inschrijving of verlies aan follow-up.

Identificatienummer deelnemer	Jaar van overlijden	Jaar laatste contact
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Levens tabel (Actuariële tabel)

Een manier om de ervaringen van de deelnemers samen te vatten is met een levens tabel, of een actuariële tabel. Levenstafels worden vaak gebruikt in de verzekeringssector om de levensverwachting te schatten en de premies vast te stellen. Wij concentreren ons op een bepaald type sterftetabel dat veel wordt gebruikt in biostatistische analyses, namelijk een cohort sterftetabel of een follow-up sterftetabel. De opvolglevenstabel vat de ervaringen van de deelnemers samen gedurende een vooraf bepaalde opvolgingsperiode in een cohortstudie of in een klinische proef tot het tijdstip van de gebeurtenis van belang of het einde van de studie, afhankelijk van wat zich het eerst voordoet.

Om een levenstabel te construeren, ordenen we eerst de opvolgingstijden in gelijkmatig verdeelde intervallen. In de bovenstaande tabel hebben we een maximale follow-up van 24 jaar, en we beschouwen intervallen van 5 jaar (0-4, 5-9, 10-14, 15-19 en 20-24 jaar). We tellen het aantal deelnemers op die in leven zijn aan het begin van elk interval, het aantal dat overlijdt, en het aantal dat gecensureerd wordt in elk interval.

Interval in jaren	Aantal in leven aan het begin van interval	Aantal sterfgevallen tijdens interval	Aantal gecensureerd
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

Wij gebruiken de volgende notatie in onze analyse van de levenstabel. Wij definiëren eerst de notatie en gebruiken deze vervolgens om de tabel op te stellen.

• Nt = aantal deelnemers die gebeurtenisvrij zijn en geacht worden risico te lopen gedurende interval t (bijv, in dit voorbeeld het aantal levenden aangezien onze uitkomst van belang de dood is)
• Dt = aantal deelnemers dat sterft (of de gebeurtenis van belang ondergaat) tijdens interval t
• Ct = aantal deelnemers dat gecensureerd wordt tijdens interval t Nt* = het gemiddelde aantal deelnemers dat risico loopt tijdens interval t
• Nt* = het gemiddelde aantal deelnemers dat risico loopt tijdens interval t [Bij het construeren van actuariële sterftetafels worden vaak de volgende veronderstellingen gemaakt: Ten eerste, de gebeurtenissen van belang (b.v. overlijden) worden verondersteld plaats te vinden aan het eind van het interval en censored gebeurtenissen worden verondersteld gelijkmatig (of gelijkmatig) plaats te vinden gedurende het interval. Daarom wordt Nt vaak gecorrigeerd om het gemiddelde aantal deelnemers weer te geven dat gedurende het interval risico loopt, Nt*, dat als volgt wordt berekend: Nt* =Nt-Ct/2 (d.w.z,
• qt = aandeel dat sterft (of een gebeurtenis ondergaat) tijdens interval t, qt = Dt/Nt*
• pt = aandeel dat interval t overleeft (gebeurtenisvrij blijft), pt = 1-qt
• St, het aandeel dat voorbij interval t overleeft (of gebeurtenisvrij blijft); dit wordt soms de cumulatieve overlevingskans genoemd en deze wordt als volgt berekend: Eerst wordt het percentage deelnemers dat na tijdstip 0 (het begintijdstip) overleeft, gedefinieerd als S0 = 1 (alle deelnemers in leven of vrij van voorvallen op tijdstip nul of begin van het onderzoek). Het percentage deelnemers dat elk volgend interval overleeft, wordt berekend met behulp van de beginselen van voorwaardelijke waarschijnlijkheid die in de module over waarschijnlijkheid zijn geïntroduceerd. Meer bepaald is de kans dat een deelnemer na interval 1 overleeft S1 = p1. De kans dat een deelnemer voorbij interval 2 overleeft, betekent dat hij voorbij interval 1 en door interval 2 moest overleven: S2 = P(overleef voorbij interval 2) = P(overleef voorbij interval 2)*P(overleef voorbij interval 1), of S2 = p2*S1. In het algemeen geldt: St+1 = pt+1*St.

De opmaak van de vervolgleeftijdtabel is hieronder weergegeven.

Voor het eerste interval, 0-4 jaar: Op tijdstip 0, het begin van het eerste interval (0-4 jaar), zijn er 20 deelnemers in leven of in gevaar. Twee deelnemers overlijden in het interval en 1 wordt gecensureerd. We passen de correctie toe voor het aantal deelnemers dat in dat interval wordt gecensureerd, zodat Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. De berekeningen van de overige kolommen staan in de tabel. De kans dat een deelnemer na 4 jaar, of na het eerste interval (waarbij de bovengrens van het interval wordt gebruikt om de tijd te definiëren) overleeft, is S4 = p4 = 0,897.

Voor het tweede interval, 5-9 jaar: Het aantal risicodragers is het aantal risicodragers in het vorige interval (0-4 jaar) min degenen die sterven en gecensureerd worden (d.w.z. Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). De kans dat een deelnemer langer dan 9 jaar overleeft is S9 = p9*S4 = 0,937*0,897 = 0,840.

Interval in jaren	Aantal risicopersonen tijdens interval, Nt	Gemiddeld aantal risicopersonen tijdens interval, Nt*	Aantal sterfgevallen tijdens interval, Dt	Verloren voor follow-up, Ct	Deel sterfgevallen tijdens interval, qt	Onder degenen die risico liepen, het deel dat overleefde Interval, pt	Overlevingskans St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

De volledige vervolgleeftijdtabel is hieronder weergegeven.

Interval in jaren	Aantal risicopersonen tijdens interval, Nt	Gemiddeld aantal risicopersonen tijdens interval, Nt*	Aantal sterfgevallen tijdens interval, Dt	Verloren voor follow-up, Ct	Proportion Dying During Interval, qt	Am among those at Risk, Proportion Surviving Interval, pt	Survival Probability St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Deze tabel maakt gebruik van de actuariële methode om de vervolglevensverwachtingstabel te construeren waarbij de tijd in gelijkmatig verdeelde intervallen is verdeeld.

Kaplan-Meier (Product Limit) Approach

Een probleem met de hierboven getoonde levenstabel-benadering is dat de overlevingskansen kunnen veranderen afhankelijk van hoe de intervallen zijn georganiseerd, vooral bij kleine steekproeven. De Kaplan-Meier-benadering, ook wel de productlimietbenadering genoemd, is een populaire benadering die dit probleem aanpakt door de overlevingskans opnieuw te schatten telkens wanneer zich een gebeurtenis voordoet.

Geschikt gebruik van de Kaplan-Meier-benadering berust op de aanname dat censuur onafhankelijk is van de waarschijnlijkheid van het ontwikkelen van de gebeurtenis van belang en dat de overlevingskansen vergelijkbaar zijn bij deelnemers die vroeg en later in de studie worden gerekruteerd. Wanneer verschillende groepen worden vergeleken, is het ook belangrijk dat in elke vergelijkingsgroep aan deze veronderstellingen wordt voldaan en dat bijvoorbeeld de kans op censuur in de ene groep niet groter is dan in de andere.

In de onderstaande tabel worden met behulp van de Kaplan-Meier-benadering dezelfde gegevens gepresenteerd als hierboven met behulp van de levensdetabelbenadering. Merk op dat we de tabel beginnen met Tijd=0 en Overlevingskans = 1. Op Tijd=0 (basislijn, of het begin van de studie) lopen alle deelnemers risico en is de overlevingskans 1 (of 100%). Met de Kaplan-Meier-methode wordt de overlevingskans berekend met St+1 = St*((Nt+1-Dt+1)/Nt+1). Merk op dat de berekeningen volgens de Kaplan-Meier-methode vergelijkbaar zijn met die volgens de actuariële sterftetabelmethode. Het belangrijkste verschil zijn de tijdsintervallen, d.w.z. bij de actuariële sterftetabelbenadering gaan we uit van intervallen met gelijke tussenpozen, terwijl we bij de Kaplan-Meier-benadering uitgaan van waargenomen gebeurtenistijden en censortijden. De berekeningen van de overlevingskansen worden gedetailleerd weergegeven in de eerste paar rijen van de tabel.

Levensduur volgens de Kaplan-Meier-benadering

Tijd, Jaren	Aantal risicogevallen Nt	Aantal sterfgevallen Dt	aantal gecensureerd Ct	overlevingskans St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20			1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3	3	0,507

Bij grote gegevensverzamelingen zijn deze berekeningen omslachtig. Deze analyses kunnen echter worden gegenereerd door statistische rekenprogramma’s zoals SAS. Excel kan ook worden gebruikt om de overlevingskansen te berekenen, zodra de gegevens zijn geordend naar tijdstippen en de aantallen gebeurtenissen en gecensureerde tijdstippen zijn samengevat.

Uit de overlevingstabel kunnen we een Kaplan-Meier overlevingscurve afleiden.

Kaplan-Meier overlevingscurve voor de bovenstaande gegevens

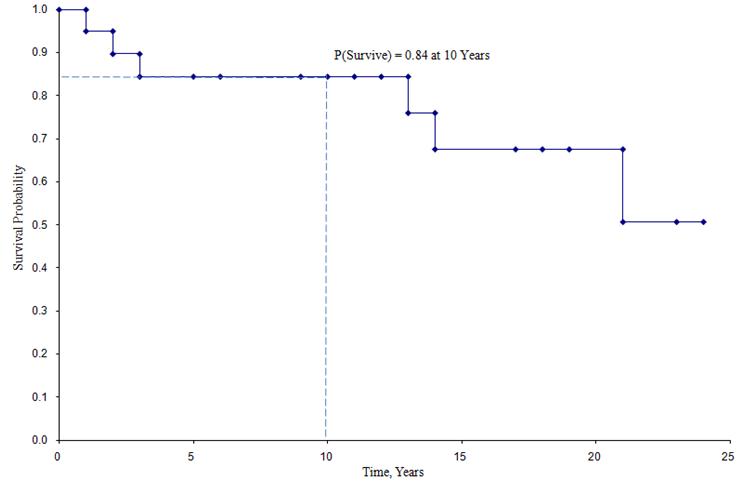
In de hierboven getoonde overlevingskromme stellen de symbolen elk tijdstip van een gebeurtenis voor, hetzij een sterfgeval of een gecensureerd tijdstip. Aan de hand van de overlevingscurve kan ook worden geschat hoe groot de kans is dat een deelnemer langer dan 10 jaar overleeft door 10 jaar op de X-as te zetten en naar boven en over de Y-as te lezen. Het percentage deelnemers dat langer dan 10 jaar overleeft is 84%, en het percentage deelnemers dat langer dan 20 jaar overleeft is 68%. De mediane overleving wordt geschat door 0,5 op de Y-as te plaatsen en over en neer op de X-as af te lezen. De mediane overleving is ongeveer 23 jaar.

Standaardfouten en betrouwbaarheidsintervalschattingen van overlevingskansen

Deze schattingen van overlevingskansen op specifieke tijdstippen en de mediane overlevingstijd zijn puntschattingen en moeten als zodanig worden geïnterpreteerd. Er zijn formules om standaardfouten en betrouwbaarheidsintervalschattingen van overlevingskansen te produceren die met veel statistische rekenpakketten kunnen worden gegenereerd. Een populaire formule om de standaardfout van de overlevingsschattingen te schatten heet de Greenwoods5 formule en is als volgt:

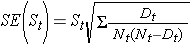
De hoeveelheid 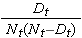wordt gesommeerd voor aantallen risicogevallen (Nt) en aantallen sterfgevallen (Dt) die zich voordoen gedurende het tijdstip van belang (d.w.z. cumulatief, over alle tijdstippen vóór het tijdstip van belang, zie voorbeeld in de tabel hieronder). Standaardfouten worden berekend voor de overlevingsschattingen voor de gegevens in de onderstaande tabel. Merk op dat in de laatste kolom de grootheid 1,96*SE(St) staat, die de foutenmarge is en gebruikt wordt voor de berekening van de 95%-schattingen van het betrouwbaarheidsinterval (d.w.z. St ± 1,96 x SE(St)).

Standaardfouten van overlevingsschattingen

Tijd, Jaren	aantal risicopersonen Nt	aantal sterfgevallen Dt	overlevingskans Waarschijnlijkheid St				1.96*SE (St)
0	20		1
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0,000	0,118	0,174	0,341

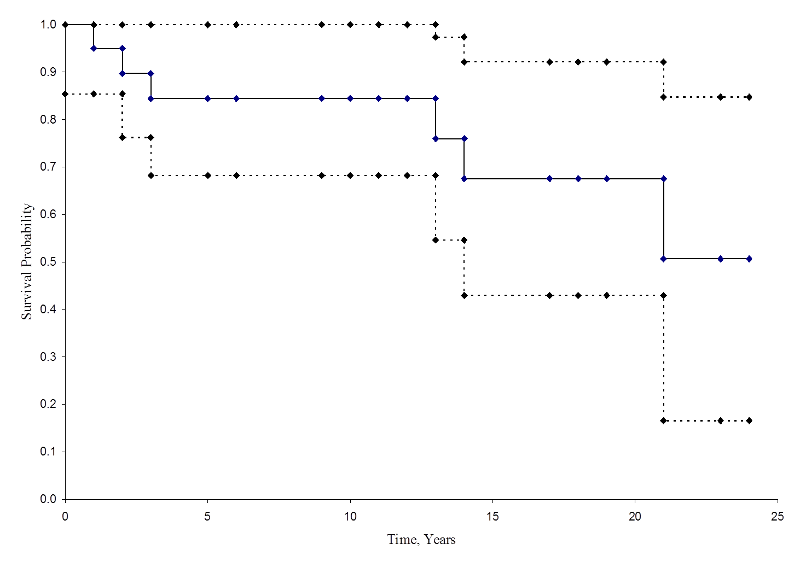
In de onderstaande figuur zijn de schattingen en betrouwbaarheidsintervallen samengevat. De Kaplan-Meier-overlevingscurve wordt weergegeven als een ononderbroken lijn, en de 95%-betrouwbaarheidsgrenzen worden weergegeven als stippellijnen.

Kaplan-Meier-overlevingscurve met betrouwbaarheidsintervallen

Cumulatieve incidentiecurven

Sommige onderzoekers geven er de voorkeur aan cumulatieve incidentiecurven te genereren, in tegenstelling tot overlevingscurven die de cumulatieve waarschijnlijkheid van het doormaken van de gebeurtenis van belang weergeven. Cumulatieve incidentie, of cumulatieve faalkans, wordt berekend als 1-St en kan gemakkelijk uit de levenstabel worden berekend met behulp van de Kaplan-Meier-methode. De cumulatieve faalkansen voor bovenstaand voorbeeld staan in onderstaande tabel.

Levensduurtabel met cumulatieve faalkansen

Tijd, Jaren	aantal risico’s Nt	aantal sterfgevallen Dt	aantal Gecensureerd Ct	Overlevingskans St	Overlevingskans 1-St
0	20		1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0.493

De onderstaande figuur toont de cumulatieve incidentie van overlijden voor deelnemers die aan de hierboven beschreven studie hebben deelgenomen.

Cumulatieve incidentiecurve

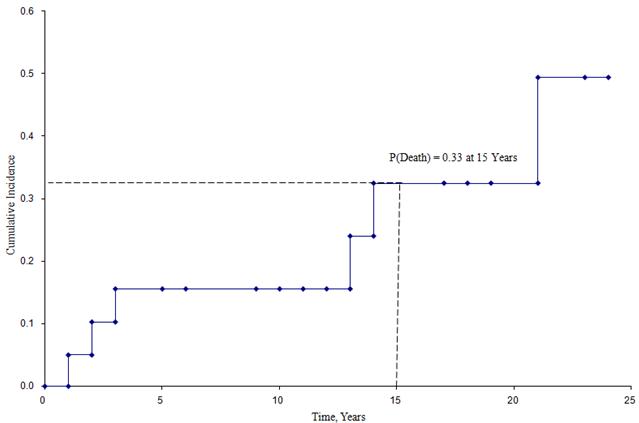
Uit deze figuur kunnen we schatten hoe groot de kans is dat een deelnemer op een bepaald tijdstip overlijdt. De kans op overlijden is bijvoorbeeld ongeveer 33% op 15 jaar (zie de stippellijnen).

terug naar boven | vorige pagina | volgende pagina