Kolmogorov-Smirnov Test
De K-S test is een goodness-of-fit test die wordt gebruikt om de uniformiteit van een reeks van gegevensverdelingen te beoordelen. Hij werd ontworpen als antwoord op de tekortkomingen van de chi-kwadraattoets, die alleen nauwkeurige resultaten oplevert voor discrete, gekwantificeerde verdelingen. De K-S-toets heeft het voordeel dat hij geen aannames doet over de binning van de te vergelijken gegevensverzamelingen, waardoor het arbitraire karakter en het verlies van informatie, dat gepaard gaat met het proces van bin-selectie, wordt weggenomen.
In de statistiek is de K-S-toets de geaccepteerde toets voor het meten van verschillen tussen continue gegevensverzamelingen (ongebunkerde gegevensverdelingen) die een functie zijn van een enkele variabele. Deze verschilmaat, de K-S statistiek, wordt gedefinieerd als de maximale waarde van het absolute verschil tussen twee cumulatieve verdelingsfuncties. De eenzijdige K-S-toets wordt gebruikt om een gegevensreeks te vergelijken met een bekende cumulatieve verdelingsfunctie, terwijl de tweezijdige K-S-toets twee verschillende gegevensreeksen vergelijkt. Elke gegevensverzameling geeft een andere cumulatieve verdelingsfunctie, en de betekenis daarvan ligt in de relatie tot de kansverdeling waaruit de gegevensverzameling is afgeleid: de kansverdelingsfunctie voor één onafhankelijke variabele is een functie die een kans toekent aan elke waarde van \(x\). De kans die de specifieke waarde \(x_{i})aanneemt, is de waarde van de kansverdelingsfunctie bij \(x_{i})en wordt aangeduid met \(P(x_{i})\).De cumulatieve verdelingsfunctie is gedefinieerd als de functie die de fractie van gegevenspunten links van een bepaalde waarde (x_{i}) geeft, \(P(x <x_{i})\); zij geeft de kans weer dat \(x}) kleiner is dan of gelijk is aan een bepaalde waarde \(x_{i})\).
Voor het vergelijken van twee verschillende cumulatieve verdelingsfuncties \(S_{N1}(x)\) en \(S_{N2}(x)\) is de K-S statistiek
D = max|S_N1(x) – S_N2(x)|
waarbij \(S_{N}(x)\) de cumulatieve verdelingsfunctie is van de kansverdeling waaruit een dataset met \(N)\) gebeurtenissen wordt getrokken. Als \(N\) geordende gebeurtenissen zich bevinden op datapunten \(x_{i}\), waarbij \(i = 1, \, N\), dan
S_N(x_i) = (i-N)/N
waarbij de \(x\) data-array in oplopende volgorde is gesorteerd. Dit is een stapfunctie die bij de waarde van elk geordend gegevenspunt met \(1/N\) toeneemt.
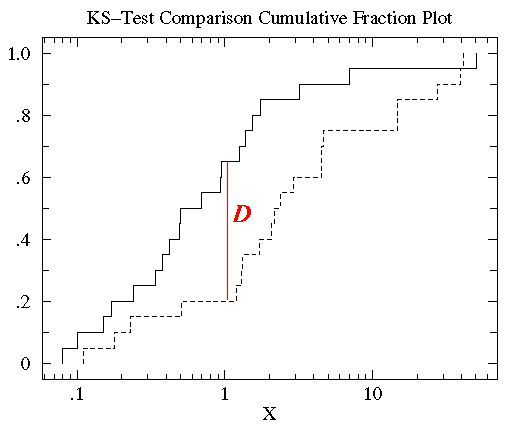
Kirkman, T.W. (1996) Statist to Use.
http://www.physics.csbsju.edu/stats/
Voor onze doeleinden zijn de twee vergeleken verdelingen de gemeten verdeling van de aankomsttijden, en de gecumuleerde fractie over het verstreken tijdsinterval. Als de nulhypothese (geen variabiliteit) geldt, krijgen we 50% van de gebeurtenissen in 50% van de verstreken tijd, en de statistiek zou zich moeten verdelen volgens de Kolmogorov-verdeling voor vele realisaties van de aankomsttijdenverdeling. De kans die de test oplevert is dus (p_{KS} = 1 – \alpha), waarbij \(\alpha) de kans is (onder de Kolmogorov verdeling) dat de waarde van \(D\) groter of gelijk is aan de gemeten waarde. Een kleine waarde van \(p_{KS}}) wijst dus op overeenstemming met de nulhypothese, terwijl een grote waarde van \(p_{KS}}) aangeeft dat het interval tussen de gebeurtenissen niet constant is, en dat er dus variabiliteit uit kan worden afgeleid.