De StatsTest Flow: Voorspelling >> Continue afhankelijke variabele >> Meer dan één onafhankelijke variabele >> Geen herhaalde metingen >> Eén afhankelijke variabele

Niet zeker of dit de juiste statistische methode is? Gebruik de workflow Choose Your StatsTest om de juiste methode te selecteren.

Wat is Multivariate Meervoudige Lineaire Regressie?

Multivariate Meervoudige Lineaire Regressie is een statistische test die wordt gebruikt om meerdere uitkomstvariabelen te voorspellen met behulp van een of meer andere variabelen. Hij wordt ook gebruikt om de numerieke relatie tussen deze reeksen variabelen en andere te bepalen. De variabele die u wilt voorspellen moet continu zijn en uw gegevens moeten voldoen aan de andere aannames die hieronder worden genoemd.

Aannames voor Multivariate Meervoudige Lineaire Regressie

Elke statistische methode heeft aannames. Veronderstellingen houden in dat uw gegevens aan bepaalde eigenschappen moeten voldoen, willen de resultaten van de statistische methode nauwkeurig zijn.

De veronderstellingen voor Multivariate Multiple Linear Regression omvatten:

1. Lineariteit
2. Geen uitschieters
3. Gelijkmatige spreiding over het bereik
4. Normaliteit van Residuen
5. Geen Multicollineariteit

Laten we eens in elk van deze afzonderlijk duiken.

Lineariteit

De variabelen waar het om gaat moeten lineair aan elkaar gerelateerd zijn. Dit betekent dat als u de variabelen uitzet, u een rechte lijn kunt trekken die past bij de vorm van de gegevens.

Geen uitschieters

De variabelen waar het om gaat, mogen geen uitschieters bevatten. Lineaire regressie is gevoelig voor uitschieters, of gegevenspunten die ongewoon grote of kleine waarden hebben. U kunt zien of uw variabelen uitschieters bevatten door ze uit te zetten en te kijken of er punten zijn die ver van alle andere punten liggen.

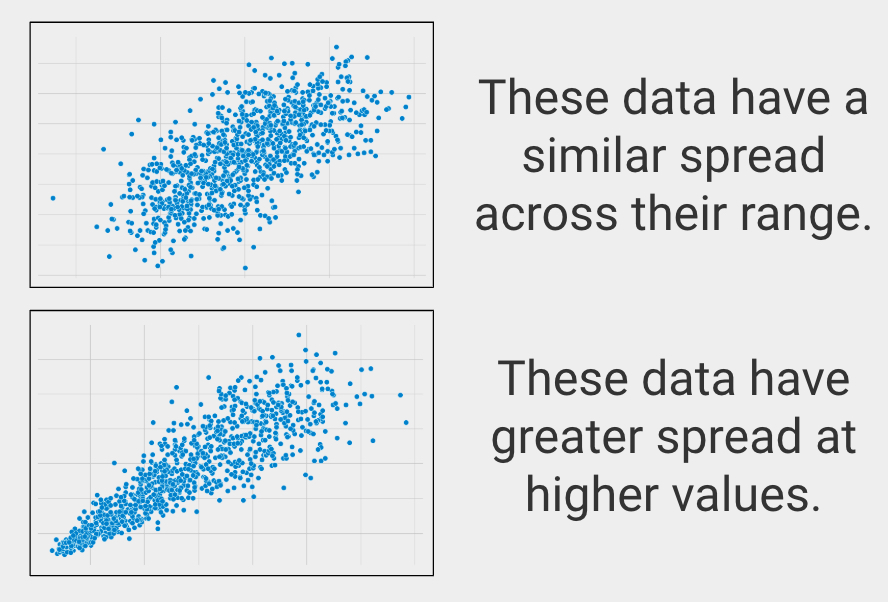
Gelijkmatige spreiding over het bereik

In de statistiek heet dit homoscedasticiteit, die beschrijft wanneer variabelen een gelijkmatige spreiding over hun bereik hebben.

Normaliteit van residuen

Het woord “residuen” verwijst naar de waarden die resulteren uit het aftrekken van de verwachte (of voorspelde) afhankelijke variabelen van de werkelijke waarden. De verdeling van deze waarden moet overeenkomen met een normale (of belcurve) verdelingsvorm.

Het voldoen aan deze aanname verzekert dat de resultaten van de regressie gelijkelijk van toepassing zijn over de gehele spreiding van de gegevens en dat er geen systematische vertekening in de voorspelling optreedt.

Geen multicollineariteit

Multicollineariteit verwijst naar het scenario waarin twee of meer van de onafhankelijke variabelen onderling aanzienlijk gecorreleerd zijn. Wanneer multicollineariteit aanwezig is, worden de regressiecoëfficiënten en de statistische significantie onstabiel en minder betrouwbaar, hoewel het geen invloed heeft op hoe goed het model op zich bij de gegevens past.

Wanneer multivariate meervoudige lineaire regressie gebruiken?

U moet Multivariate Multiple Linear Regression in het volgende scenario gebruiken:

1. U wilt één variabele gebruiken in een voorspelling van meerdere andere variabelen, of u wilt de numerieke relatie tussen deze variabelen kwantificeren
2. De variabelen die u wilt voorspellen (uw afhankelijke variabele) zijn continu
3. U hebt meer dan één onafhankelijke variabele, of één variabele die u als voorspeller gebruikt
4. U hebt geen herhaalde metingen van dezelfde eenheid van waarneming
5. U hebt meer dan één afhankelijke variabele

Laten we deze verduidelijken om u te helpen weten wanneer u Multivariate Meervoudige Lineaire Regressie moet gebruiken.

Voorspelling

U bent op zoek naar een statistische test om een variabele te voorspellen aan de hand van een andere variabele. Dit is een voorspellingsvraag. Andere soorten analyses zijn het onderzoeken van de sterkte van het verband tussen twee variabelen (correlatie) of het onderzoeken van verschillen tussen groepen (verschil).

Continue Afhankelijke Variabele

De variabele die u wilt voorspellen moet continu zijn. Continu betekent dat uw variabele in principe elke waarde kan aannemen, zoals hartslag, lengte, gewicht, aantal repen ijs dat u in 1 minuut kunt eten, enz.

Typen gegevens die NIET continu zijn, zijn geordende gegevens (zoals plaats in een race, beste bedrijfsranglijst, enz.), categorische gegevens (geslacht, oogkleur, ras, enz.), of binaire gegevens (het product gekocht of niet, de ziekte gehad of niet, enz.).

Als uw afhankelijke variabele binair is, moet u gebruikmaken van meervoudige logistische regressie, en als uw afhankelijke variabele categorisch is, moet u gebruikmaken van multinomiale logistische regressie of lineaire discriminantanalyse.

Meer dan één onafhankelijke variabele

Multivariate Meervoudige Lineaire Regressie wordt gebruikt wanneer er sprake is van één of meer voorspellende variabelen met meerdere waarden voor elke eenheid van waarneming.

Geen herhaalde metingen

Deze methode is geschikt voor het scenario waarin er slechts één waarneming is voor elke eenheid van waarneming. De eenheid van waarneming is wat een “gegevenspunt” vormt, bijvoorbeeld een winkel, een klant, een stad, enz…

Als u een of meer onafhankelijke variabelen hebt, maar deze voor dezelfde groep op meerdere tijdstippen worden gemeten, moet u een Mixed Effects Model gebruiken.

Meer dan één afhankelijke variabele

Om Multivariate Multiple Linear Regression uit te voeren, moet u meer dan één afhankelijke variabele hebben, of variabele die u probeert te voorspellen.

Als u slechts één variabele voorspelt, moet u Multiple Linear Regression gebruiken.

Multivariate Multiple Linear Regression Voorbeeld

Dependent Variable 1: Inkomsten
Debepalende Variabele 2: Klantenverkeer
Afhankelijke Variabele 1: Dollars uitgegeven aan reclame per stad
Afhankelijke Variabele 2: Bevolking per stad

De nulhypothese, wat statistisch jargon is voor wat er zou gebeuren als de behandeling niets doet, is dat er geen verband is tussen de uitgaven aan reclame en de reclamedollars of de bevolking per stad. Onze test beoordeelt de waarschijnlijkheid dat deze hypothese waar is.

We verzamelen onze gegevens en nadat we hebben vastgesteld dat aan de veronderstellingen van lineaire regressie is voldaan, voeren we de analyse uit.

Deze analyse voert in feite tweemaal meervoudige lineaire regressie uit met beide afhankelijke variabelen. Wanneer wij deze analyse uitvoeren, krijgen wij dus bètacoëfficiënten en p-waarden voor elke term in het “inkomsten”-model en in het “klantenverkeer”-model. Voor elk lineair regressiemodel hebt u één bètacoëfficiënt die gelijk is aan het intercept van uw lineaire regressielijn (vaak met een 0 aangeduid als β0). Dit is gewoon waar de regressielijn de y-as kruist als u uw gegevens zou plotten. In het geval van meervoudige lineaire regressie zijn er nog twee andere bètacoëfficiënten (β1, β2, enz.), die de relatie tussen de onafhankelijke en afhankelijke variabelen weergeven.

Deze extra bètacoëfficiënten zijn de sleutel tot het begrip van de numerieke relatie tussen uw variabelen. In wezen wordt verwacht dat voor elke eenheid (waarde van 1) toename van een bepaalde onafhankelijke variabele, uw afhankelijke variabele verandert met de waarde van de bètacoëfficiënt die aan die onafhankelijke variabele is gekoppeld (terwijl andere onafhankelijke variabelen constant worden gehouden).

De p-waarde die aan deze aanvullende bètawaarden is gekoppeld, is de kans dat onze resultaten worden gezien in de veronderstelling dat er in feite geen relatie is tussen die variabele en de omzet. Een p-waarde kleiner dan of gelijk aan 0,05 betekent dat ons resultaat statistisch significant is en dat we erop kunnen vertrouwen dat het verschil niet aan toeval alleen te wijten is. Om een algemene p-waarde voor het model te krijgen en individuele p-waarden die de effecten van variabelen over de twee modellen weergeven, worden vaak MANOVA’s gebruikt.

Daarnaast zal deze analyse resulteren in een R-Squared (R2)-waarde. Deze waarde kan variëren van 0-1 en geeft aan hoe goed uw lineaire regressielijn bij uw gegevenspunten past. Hoe hoger de R2, hoe beter uw model bij uw gegevens past.

Veelgestelde vragen

Q: Wat is het verschil tussen multivariate meervoudige lineaire regressie en het meervoudig uitvoeren van lineaire regressie?
A: Ze zijn conceptueel vergelijkbaar, aangezien de afzonderlijke modelcoëfficiënten in beide scenario’s hetzelfde zullen zijn. Een wezenlijk verschil is echter dat significantietests en betrouwbaarheidsintervallen voor multivariate lineaire regressie rekening houden met de meervoudige afhankelijke variabelen.

Q: Hoe voer ik multivariate meervoudige lineaire regressie uit in SPSS, R, SAS of STATA?
A: Deze bron is erop gericht u te helpen elke keer de juiste statistische methode te kiezen. Er zijn veel bronnen beschikbaar om u te helpen uitzoeken hoe u deze methode met uw gegevens kunt toepassen:
R artikel: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Help!

Als u er nog steeds niet uitkomt, neem dan gerust contact met ons op.