Tetraëder

Inhoud van deze pagina Wat is een Tetraëder? Delen van de Tetraëder Tetraëdergetallen Tetraëder in de kubus Ringen van Tetraëders Tetraëders op hetInternet

Naar de hoofdpagina “Mathematische Basteleien”

Wat is een Tetraëder?

Een tetraëder is een driedimensionale figuur met vier gelijkzijdige driehoeken. Als je drie driehoeken optilt (1), krijg je de tetraëder in bovenaanzicht (2). Over het algemeen wordt hij in perspectief weergegeven (3).

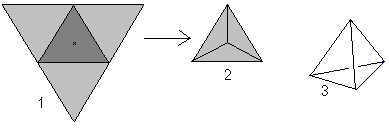
Als je naar het woord tetraëder kijkt (tetraëder betekent “met vier vlakken”), dan zou je elke piramide met een driehoek als basis een tetraëder kunnen noemen.

De tetraëder is echter de rechte, regelmatige driehoekige piramide op deze website.

Delen van deTetraëdertop
Hoogte en oppervlakte van een zijdriehoek
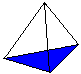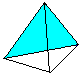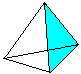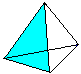
Vier gelijkzijdige driehoeken vormen een tetraëder.

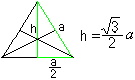…	Een driehoek is uitgekozen: De drie hoogten snijden elkaar in één punt, zoals in elke driehoek. Dit is het middelpunt van de driehoek. De hoogte kan worden berekend door de zijde a als h=sqr(3)/2*a met behulp van de stelling van Pythagoras.

De hoogten zijn ook medianen en snijden elkaar met de verhouding 2:1. Die wordt in de volgende berekeningen gebruikt.

De oppervlakte van de driehoek is A=sqr(3)/4*a².

Ruimtehoogte

De hoogte van de tetraëder ligt tussen het middelpunt van de basisdriehoek (1) en het hoekpunt (2). Voor berekeningen beschouwt men de zogenaamde steundriehoek (3, geel), die gevormd wordt door één zijde en twee driehoekshoogten. Er geldt H=sqr(6)/3*a met behulp van de Pythagorasantheorema.
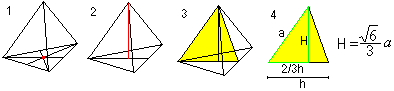
Centrum, omgeschreven bol en ingeschreven bol Het middelpunt van een tetraëder is het snijpunt van twee ruimtehoogten (1,2,3). Het is het zwaartepunt, middelpunt van de bol door de vier hoeken, en middelpunt van de grootste bol, die nog in de tetraëder past (4).

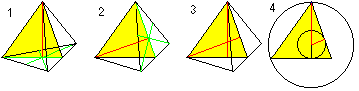
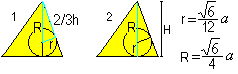…	U krijgt twee formules voor r en R met behulp van de stelling van Pythagoras (1) en H=R+r (2): Er is r=sqr(6)/12*a , R=sqr(6)/4*a.

Hoekoppervlak

….…..

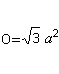De oppervlakte van het grondvlak en de zijvlakken vormen het oppervlakO. Er is O=4*A (driehoek) = sqr(3)a².

Volume

Tetrahedaalgetallen top

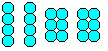…….	Als je 20 knikkers plakt in twee groepen met vier en twee met zes, krijg je een bekende puzzel: Je moet een piramide vormen met vier stukken.

Er zijn veel soortgelijke puzzels.

Tetraëder in de kubus top
Zes gezichtsdiagonalen vormen een tetraëder in de kubus.
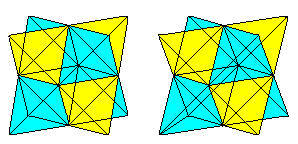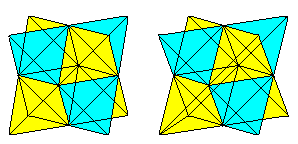
Als u het 3D-beeld kent, kunt u de volgende twee kubusparen driedimensionaal bekijken.

Het volume van de tetraëder is het derde deel van het volume van de kubus.

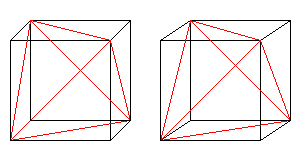
Als u een tweede tetraëder en de snijlijnen tekent, krijgt u een doorsnede van twee tetraëders.

De figuur bestaat uit de gezichtsdiagonalen en de verbindingslijnen van de middelpunten van de laterale vierkanten van de oorspronkelijke kubus. De laatste tonen vormen een octaëder.

Ringen van tetraëders top
Je kunt papieren tetraëders maken en daar een even aantal van op een ring plakken. De ring kan voortdurend door het midden naar binnen of naar buiten draaien. Dit is leuk speelgoed. – Deze ringen worden ook wel kaleidocyclles genoemd. Meer hierover op mijn webpagina Kaleidocycles.

Tetrahedraon the Internettop

German

Christof Weber
Wat doet dieer Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

Engels

Eric W. Weisstein (World of Mathematics)
Tetraëder

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraëder

Joyce Frost en Peg Cagle (mathforum)
Een verbluffende, ruimtevullende, niet-regelmatige tetraëder

Wikipedia
Tetraëder,Tetrapod(structuur), Tetraëdernummer