Graphs in Python

Origins of Graph Theory

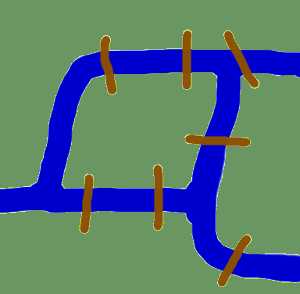Voordat we beginnen met de eigenlijke implementaties van grafieken in Python en voor we beginnen met de introductie van Python-modules die zich met grafieken bezighouden, willen we ons wijden aan de oorsprong van de grafentheorie.
De oorsprong brengt ons terug in de tijd naar het Künigsberg van de 18e eeuw. Königsberg was in die tijd een stad in Pruisen. De rivier de Pregel stroomde door de stad, waardoor twee eilanden ontstonden. De stad en de eilanden waren met elkaar verbonden door zeven bruggen, zoals afgebeeld. De inwoners van de stad werden geraakt door de vraag, of het mogelijk was een wandeling door de stad te maken door elk deel van de stad te bezoeken en elke brug slechts één keer over te steken? Elke brug moet volledig zijn overgestoken, d.w.z. het is niet toegestaan om halverwege een brug te lopen en dan om te keren en later de andere helft vanaf de andere kant over te steken. De wandeling hoeft niet op dezelfde plaats te beginnen en te eindigen.Leonhard Euler loste het probleem in 1735 op door te bewijzen dat het niet mogelijk is. Hij ontdekte dat de keuze van een route binnen elk landgebied irrelevant is en dat het enige dat telt de volgorde (of de volgorde) is waarin de bruggen worden overgestoken. Hij had een abstractie van het probleem gemaakt door overbodige feiten te elimineren en zich te concentreren op de landgebieden en de bruggen die ze verbinden. Op deze manier schiep hij de grondslagen van de grafentheorie. Als we een “landgebied” als een hoekpunt zien en elke brug als een rand, hebben we het probleem “gereduceerd” tot een grafiek.

Inleiding in de grafentheorie met behulp van Python

Voordat we beginnen met onze behandeling van mogelijke Python-weergaven van grafieken, willen we eerst enkele algemene definities van grafieken en de componenten ervan presenteren.
Een “grafiek “1 in de wiskunde en informatica bestaat uit “knooppunten”, ook wel “hoekpunten” genoemd.Knooppunten kunnen al dan niet met elkaar verbonden zijn. In onze illustratie, – die een grafische voorstelling van een grafiek is, – is het knooppunt “a” verbonden met het knooppunt “c”, maar “a” is niet verbonden met “b”. De verbindingslijn tussen twee knooppunten wordt een rand genoemd. Als de ribben tussen de knopen ongericht zijn, heet de grafiek een ongerichte grafiek. Als een rand van een hoekpunt (node) naar een ander hoekpunt (node) is gericht, heet een grafiek een gerichte grafiek. Een gerichte rand heet een arc.

Hoe theoretisch grafieken er ook uitzien, veel praktische problemen kunnen door grafieken worden weergegeven. Ze worden vaak gebruikt om problemen of situaties in de natuurkunde, biologie, psychologie en vooral in de informatica te modelleren. In de informatica worden grafieken gebruikt om communicatienetwerken, de organisatie van gegevens, rekenapparatuur en het verloop van berekeningen weer te geven,
In het laatste geval worden ze gebruikt om de organisatie van gegevens weer te geven, zoals het bestandssysteem van een besturingssysteem, of communicatienetwerken. De linkstructuur van websites kan ook worden gezien als een grafiek, d.w.z. een gerichte grafiek, omdat een link een gerichte edge of een arc is.
Python heeft geen ingebouwd datatype of klasse voor grafieken, maar het is gemakkelijk om ze in Python te implementeren. Eén datatype is ideaal om grafieken in Python te representeren, namelijk dictionaries. De grafiek in onze illustratie kan op de volgende manier worden geïmplementeerd:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

De sleutels van het bovenstaande woordenboek zijn de knooppunten van onze grafiek. De overeenkomstige waarden zijn lijsten met de knooppunten, die door een rand met elkaar worden verbonden. Er is geen eenvoudiger en eleganter manier om een grafiek weer te geven.
Een rand kan worden gezien als een 2-tupel met knooppunten als elementen, d.w.z. (“a”, “b”)
Functie om de lijst van alle randen te genereren:Deze code genereert de volgende uitvoer, indien gecombineerd met het eerder gedefinieerde grafiekwoordenboek:

 $ python3 graph_simple.py 

Zoals we kunnen zien, is er geen rand die het knooppunt “f” bevat. “f” is een geïsoleerd knooppunt van onze grafiek.
De volgende Python-functie berekent de geïsoleerde knooppunten van een gegeven grafiek:Als we deze functie met onze grafiek aanroepen, wordt een lijst met “f” geretourneerd:

Grafieken als Python-klasse

Voordat we verder gaan met het schrijven van functies voor grafieken, doen we eerst een poging tot een Python-implementatie van de grafiekklasse. Als je naar de volgende listing van onze klasse kijkt, zie je in de __init__-methode dat we een dictionary “self.__graph_dict” gebruiken voor het opslaan van de hoekpunten en hun corresponderende aangrenzende hoekpunten.
Als u deze module standalone start, krijgt u het volgende resultaat:

Paden in grafieken

We willen nu het kortste pad van een knooppunt naar een ander knooppunt vinden. Voordat we naar de Python-code voor dit probleem gaan, moeten we eerst enkele formele definities geven.

Aaangrenzende hoekpunten:
Twee hoekpunten zijn aangrenzend als ze beide een gemeenschappelijke flank hebben.
Pad in een ongerichte grafiek:
Een pad in een ongerichte grafiek is een reeks hoekpunten P = ( v1, v2, …., vn ) ∈ V x V x … x V zo dat vi grenst aan v{i+1} voor 1 ≤ i < n. Zo’n pad P heet een pad van lengte n van v1 naar vn.
Eenvoudig pad:
Een pad zonder herhaalde hoekpunten wordt een eenvoudig pad genoemd.
Voorbeeld:
(a, c, e) is een eenvoudig pad in onze grafiek, evenals (a,c,e,b). (a,c,e,b,c,d) is een pad, maar geen eenvoudig pad, omdat het knooppunt c twee keer voorkomt.
De volgende methode vindt een pad van een begin- naar een eindpunt:Als we onze grafiekklasse inclusief de methode find_path opslaan als “graphs.py”, kunnen we de werking van onze functie find_path controleren:Het resultaat van het vorige programma ziet er als volgt uit:
De methode find_all_paths vindt alle paden tussen een begin- en een eindpunt:We hebben onze voorbeeldgrafiek enigszins gewijzigd door randen toe te voegen van “a” naar “f” en van “f” naar “d” om de eerder gedefinieerde methode te testen:Het resultaat ziet er als volgt uit:

Graad

De graad van een hoekpunt v in een grafiek is het aantal randen dat het met elkaar verbindt, waarbij lussen twee keer worden geteld. De graad van een hoekpunt v wordt aangeduid met deg(v). De maximale graad van een grafiek G, aangeduid met Δ(G), en de minimale graad van een grafiek, aangeduid met δ(G), zijn de maximale en minimale graad van zijn hoekpunten.
In de grafiek hiernaast is de maximale graad 5 bij hoekpunt c en de minimale graad 0, dat wil zeggen het geïsoleerde hoekpunt f.
Als alle graden in een grafiek gelijk zijn, is de grafiek een regelmatige grafiek.In een regelmatige grafiek zijn alle graden gelijk, en dus kunnen we spreken van de graad van de grafiek.
De graadsomformule (Handshaking lemma):
∑v &in; Vdeg(v) = 2 |E|
Dit betekent dat de som van de graden van alle hoekpunten gelijk is aan het aantal ribben vermenigvuldigd met 2.We kunnen concluderen dat het aantal hoekpunten met oneven graad even moet zijn. Deze uitspraak staat bekend als het handshaking lemma. De naam “handshaking lemma” komt van een populair wiskundig probleem: In een willekeurige groep mensen is het aantal mensen dat een oneven aantal andere mensen uit de groep een hand heeft gegeven even.
De volgende methode berekent de graad van een hoekpunt:
De volgende methode berekent een lijst met de geïsoleerde hoekpunten van een grafiek:De methoden delta en Delta kunnen worden gebruikt om respectievelijk de minimale en maximale graad van een hoekpunt te berekenen:

Graadreeks

De graadreeks van een ongerichte grafiek wordt gedefinieerd als de opeenvolging van de vertexgraden in een niet oplopende volgorde.
De volgende methode retourneert een tupel met de graadreeks van de instance-grafiek:
De gradenreeks van onze voorbeeldgrafiek is de volgende opeenvolging van gehele getallen: (5,2,1,1,1,0).
Isomorfe grafieken hebben dezelfde gradenreeks. Twee grafieken met dezelfde gradenreeks zijn echter niet noodzakelijkerwijs isomorf.
Er is de vraag of een gegeven gradenreeks kan worden gerealiseerd door een eenvoudige grafiek. De stelling van Erdös-Gallai stelt dat een niet oplopende rij van n getallen di (voori = 1, …n) de gradenreeks van een eenvoudige grafiek is als en slechts als de som van de reeks even is en aan de volgende voorwaarde is voldaan:

Implementatie van de stelling van Erdös-Gallai

Onze grafiekklasse – zie verder voor een volledige lijst – bevat een methode “erdoes_gallai” die bepaalt of een reeks aan de stelling van Erdös-Gallai voldoet. Eerst wordt nagegaan of de som van de elementen van de rij oneven is. Zo ja, dan geeft de functie False terug, omdat de stelling van Erdös-Gallai niet meer vervuld kan worden. Hierna controleren we met de statische methode is_degree_sequence of de ingevoerde rij een gradenreeks is, d.w.z. of de elementen van de rij niet oplopend zijn. Dit is een beetje overbodig, aangezien de input verondersteld wordt een gradenreeks te zijn, dus je kan deze controle achterwege laten omwille van de efficiëntie. Nu controleren we in de body van de tweede if, of aan de formule van de stelling is voldaan:
Versie zonder de overbodige gradenreeks test:

Grafendichtheid

De grafiekdichtheid wordt gedefinieerd als de verhouding tussen het aantal randen van een gegeven grafiek, en het totale aantal randen, dat de grafiek zou kunnen hebben. Met andere woorden: Het meet hoe dicht een gegeven grafiek bij een volledige grafiek ligt.
De maximale dichtheid is 1, als een grafiek compleet is. Dit is duidelijk, want het maximum aantal ribben in een grafiek hangt af van de hoekpunten en kan worden berekend als:
max. aantal ribben = ½ * |V| * ( |V| – 1 ).
Aan de andere kant is de minimale dichtheid 0, als de grafiek geen ribben heeft, d.w.z. dat het een geïsoleerde grafiek is.
Voor eenvoudige ongerichte grafieken wordt de grafiekdichtheid als volgt gedefinieerd: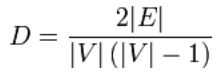

Een dichte grafiek is een grafiek waarin het aantal ribben dicht bij het maximale aantal ribben ligt. Een grafiek met slechts enkele randen wordt een schaarse grafiek genoemd. De definitie voor deze twee termen is niet erg scherp, d.w.z. er is geen kleinste bovengrens (supremum) voor een sparse dichtheid en geen grootste ondergrens (infimum) voor het definiëren van een dichte grafiek.

De nauwkeurigste wiskundige notatie gebruikt de grote O notatie:
Sparse Graph:
Dichte Grafiek:
Een dichte grafiek is een grafiek G = (V, E) waarin |E| = Θ(|V|2).
“dichtheid” is een methode van onze klasse om de dichtheid van een grafiek te berekenen:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

We kunnen deze methode testen met het volgende script. Een volledige grafiek heeft een dichtheid van 1 en een geïsoleerde grafiek heeft een dichtheid van 0, zoals we kunnen zien aan de resultaten van het vorige testscript:

$ python test_density.py 0.4666666666671.00.0

Gesloten grafieken

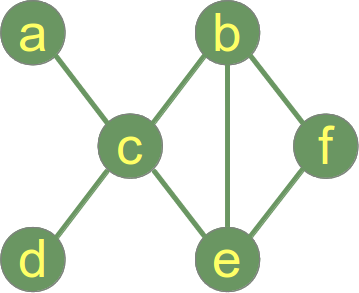Een grafiek wordt verbonden genoemd als elk paar hoekpunten in de grafiek verbonden is. De voorbeeldgrafiek hiernaast is een verbonden grafiek.
Het is mogelijk om met een eenvoudig algoritme te bepalen of een grafiek verbonden is:

1. Kies een willekeurig knooppunt x van de grafiek G als beginpunt
2. Bepaal de verzameling A van alle knooppunten die vanuit x bereikt kunnen worden.
3. Als A gelijk is aan de verzameling knopen van G, is de grafiek verbonden; anders is hij ontkoppeld.

We implementeren een methode is_connected om te controleren of een grafiek een verbonden grafiek is. We leggen de nadruk niet op efficiëntie maar op leesbaarheid.
Als u deze methode toevoegt aan onze grafiekklasse, kunnen we die testen met het volgende script. Ervan uitgaande dat je de grafiekklasse opslaat als graph2.py:
Een aangesloten component is een maximaal aangesloten deelgraf van G. Elke vertex behoort tot precies één aangesloten component, net als elke edge.

Afstand en diameter van een grafiek

De afstand “dist” tussen twee hoekpunten in een grafiek is de lengte van het kortste pad tussen deze hoekpunten. Bij de berekening van een afstand zijn geen backtracks, omwegen of lussen toegestaan.
In onze voorbeeldgrafiek rechts is de afstand tussen het hoekpunt a en het hoekpunt f 3, d.w.z. dist(a,f) = 3, omdat de kortste weg via de hoekpunten c en e (of c en b als alternatief) loopt.
De excentriciteit van een hoekpunt s van een grafiek g is de maximale afstand tot elk ander hoekpunt van de grafiek:
e(s) = max( { dist(s,v) | v ∈ V })
(V is de verzameling van alle hoekpunten van g)
De diameter d van een grafiek wordt gedefinieerd als de maximale excentriciteit van een willekeurig hoekpunt in de grafiek. Dit betekent dat de diameter gelijk is aan de lengte van het kortste pad tussen de knopen die het verst van elkaar verwijderd zijn. Om de diameter van een grafiek te bepalen, zoekt men eerst het kortste pad tussen elk tweetal hoekpunten. De grootste lengte van elk van deze paden is de diameter van de grafiek.

In onze voorbeeldgrafiek kunnen we direct zien dat de diameter 3 is, omdat de minimale lengte tussen a en f 3 is en er geen ander paar van hoekpunten is met een langer pad.
De volgende methode implementeert een algoritme om de diameter te berekenen. We kunnen de diameter van onze voorbeeldgrafiek berekenen met het volgende script, waarbij we er opnieuw van uitgaan dat onze volledige grafiekklasse is opgeslagen als graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

De waarde 3 wordt afgedrukt.

De volledige Python-grafiekklasse

In de volgende Python-code vindt u de volledige Python-klasmodule met alle besproken methoden:graph2.py

Tree / Forest

Een boom is een ongerichte grafiek die geen cycli bevat. Dit betekent dat elke twee hoekpunten van de grafiek verbonden zijn door precies één eenvoudig pad.
Een bos is een disjuncte unie van bomen. In tegenstelling tot bossen in de natuur kan een bos in de grafentheorie uit één enkele boom bestaan!
Een grafiek met één hoekpunt en geen enkele rand is een boom (en een bos).
Een voorbeeld van een boom: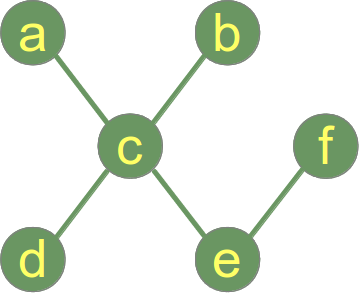

Terwijl het vorige voorbeeld een grafiek weergeeft die een boom en een bos is, toont de volgende afbeelding een grafiek die uit twee bomen bestaat, d.w.z.d.w.z. de grafiek is een bos maar geen boom:

Overzicht van bossen:

Met één hoekpunt:

Bossengrafieken met twee hoekpunten:

Bossengrafieken met drie hoekpunten:

Spannende boom

Een overspannende boom T van een verbonden, ongerichte grafiek G is een subgrafiek G’ van G, die een boom is, en G’ bevat alle hoekpunten en een deelverzameling van de ribben van G. G’ bevat alle ribben van G, als G een boomgrafiek is. Informeel is een overspannende boom van G een selectie van ribben van G die een boom vormen over elk hoekpunt. Dat wil zeggen dat elk hoekpunt in de boom ligt, maar dat er geen cycli (of lussen) in voorkomen.
Voorbeeld:
Een volledig aangesloten grafiek: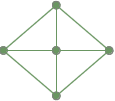

Twee overspannende bomen uit de vorige volledig aangesloten grafiek: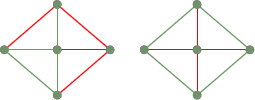

Hamiltoniaans spel

Een Hamiltoniaans pad is een pad in een ongerichte of gerichte grafiek dat elk hoekpunt precies één keer aandoet. Een Hamiltoniaanse cyclus (of circuit) is een Hamiltoniaans pad dat een cyclus is.
Noot voor informatici: Over het algemeen is het niet mogelijk om te bepalen, of dergelijke paden of cycli bestaan in willekeurige grafieken, omdat bewezen is dat het Hamiltoniaanse padprobleem NP-compleet is.
Het is vernoemd naar William Rowan Hamilton die het zogenaamde “icosiaanse spel”, of Hamilton’s puzzel, uitvond, waarbij het erom gaat een Hamiltoniaanse cyclus te vinden in de randgrafiek van de dodecaëder. Hamilton loste dit probleem op met behulp van de icosiaanse calculus, een algebraïsche structuur gebaseerd op wortels van eenheid met veel overeenkomsten met de quaternionen, die hij ook heeft uitgevonden.

Volledige lijst van de grafiekklasse

We kunnen deze grafiekklasse testen met het volgende programma:Als we dit programma starten, krijgen we de volgende uitvoer:
Voetnoten:
1 De grafieken die in de grafentheorie (en in dit hoofdstuk van onze Python-tutorial) worden bestudeerd, moeten niet worden verward met de grafieken van functies
2 Een singleton is een verzameling die precies één element bevat.
Credits:
Narayana Chikkam, nchikkam(at)gmail(dot)com, wees ons op een indexfout in de methode “erdoes_gallai”. Hartelijk dank, Narayana!