Door Evan Ma

(Docent wiskunde en natuurkunde bij The Edge Learning Center)

De logaritmische functie lijkt veel studenten die het IB Math SL programma bestuderen in verwarring te brengen. Om het goed te begrijpen, laten we

definiëren, waarbij , een strikt positief reëel getal, de basis wordt genoemd en de macht. We kennen bijvoorbeeld allemaal het volgende uit ons hoofd:

enzovoort. De logaritmische functie doet het omgekeerd – gegeven een getal als argument, levert zij de macht met een gespecificeerde basis op, en daarom is zij als volgt gedefinieerd.

Als

dan

Het is dus duidelijk dat

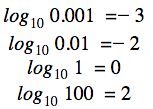
enzovoort. Laten we eens kijken naar andere voorbeelden waarbij andere basen betrokken zijn:

Laten we de volgende vragen eens invullen als oefening: (a) , (b) , (c) , (d) . De antwoorden zijn te vinden aan het eind van deze blog.

Uit de definitie van logaritme kunnen we ook opmaken dat als we het grondtal verhogen met het grondtallogaritme van een reëel getal , we het getal terugkrijgen, nl

U kunt dit proberen te controleren door uw rekenmachine te gebruiken voor verschillende geldige grondslagen. Deze identiteit is belangrijk wanneer we logaritmische vergelijkingen proberen op te lossen, waarvan voorbeelden zullen worden gegeven alter.

Nu, laten we eens kijken naar de regels van de logaritme. Vergelijkbaar met de definitie van de logaritme, gebruiken we de wetten van de indices om de regels af te leiden:

1. Logaritme van een product is som van de logaritmen

Bewijs: Zeg en , dus

2. Basis- logaritme van Mr is maal

Bewijs: Zeg , dus

3. Logaritme van een quotiënt is het verschil van logaritmen

Bewijs: Stel en , dan

4. De laatste regel heet de verandering-van-basis formule. Wij zullen een voorbeeld gebruiken als hulpmiddel om de formule af te leiden. Laten we zeggen dat we willen weten tot welke macht 2 verheven moet worden om 50 te krijgen. Aangezien 50 geen gehele macht van 2 is, ligt het antwoord niet voor de hand. Daarom schrijven we

en dus. Om te vinden, passen we logaritme base-10 toe op beide zijden van de vergelijking, aangezien onze rekenmachine wellicht niet over de base-2 logaritmetoets beschikt:

Gecorrigeerd naar 4 significante cijfers, is de waarde van ongeveer 5,644. U kunt uw antwoord controleren door 2 tot de macht van 5,644 te verheffen om te zien dat het antwoord ongeveer 50 is.

Om het probleem te veralgemenen, stel dat we moeten vinden zodanig dat en basis- logaritme ons niet ter beschikking staat, kunnen we dus in plaats daarvan base- logaritme gebruiken volgens de vergelijking

en dus

Bij wijze van voorbeeld, laten we het volgende beschouwen. Stel dat een bedrag van $10.000 wordt gedeponeerd tegen een rente van 2,5% per jaar, die jaarlijks wordt samengesteld. Hoe lang moet het geld op de rekening blijven staan om te groeien tot $50.000?

Om de vraag te beantwoorden, proberen we in feite n te vinden zodat

Aangezien mijn eenvoudige wetenschappelijke rekenmachine me niet toestaat een basis van 1 op te geven.025 voor de logaritmische sleutel, zal ik moeten vertrouwen op de formule van verandering van basis en basis-10 moeten gebruiken, en dus

Omdat de rente jaarlijks wordt samengesteld, zal het 66 jaar duren om minstens 5 keer te groeien.

Nu we de regels van logaritmen hebben verkend, introduceren we de natuurlijke logaritmische functie, of . Het is basis, waarbij het eminente irrationale getal ≈2,71828 is en waarvan het belang in de wetenschappen en de wiskunde niet genoeg kan worden benadrukt. De basislogaritme is dus als volgt gedefinieerd.

Als

dan

Laten we nu eens kijken naar twee voorbeelden waar vaak fouten worden gemaakt bij het oplossen van vergelijkingen van logaritmen. Kijk of je de fout kunt identificeren.

Waar zit de fout? Kijk beter. Natuurlijk kun je in de tweede stap het logaritme niet “splitsen” over het optelteken. Onthoud dat je een logaritme alleen in een som kunt “splitsen” als de logaritme wordt toegepast op een product, niet op een som. De juiste stappen zijn dus als volgt:

Nu kijken we naar het volgende voorbeeld en zien we of u de fout kunt identificeren:

Waar zit de fout? Ja, die zit in de tweede stap – een quotiënt van logaritmen is natuurlijk niet de logaritme van het quotiënt. In plaats daarvan kunnen we de formule van de verandering van basis gebruiken om de eerste stap te vereenvoudigen, als volgt:

Tot slot zullen we illustreren hoe we de regels van de logaritme kunnen gebruiken om het volgende op te lossen:

Je zult misschien opmerken dat de onbekende als basis en als variabele in het argument van de logaritme voorkomt. Hoe kunnen we oplossen? De methode hangt nog steeds af van het consequent toepassen van de regels van de logaritme. Eerst verheffen we beide zijden tot machten van de basis , en dus

U herinnert zich wellicht uit de definitie van logaritme dat het linkerlid gewoon het argument van het logaritme wordt, en dus

Door de bovenstaande vergelijking te herschikken, moeten we

Om te zien dat dit lijkt op een kwadratische vergelijking in , lossen we als volgt op:

Nu, waar is de negatieve wortel? Aangezien ook de basis van de logaritme is, wordt de negatieve wortel als oplossing verworpen. is dus het uiteindelijke antwoord.

Door de bovenstaande voorbeelden te bekijken, ziet u dat het oplossen van een schijnbaar moeilijke logaritmische vergelijking helemaal niet moeilijk is – u hoeft alleen maar de regels van het logaritme consequent toe te passen en de juiste oplossing kan worden verkregen.

Antwoorden op vragen: (a) 2 (b) 3 (c) -3 (d) -2.