Christian Bohr och begreppet kooperativ bindningRedigera

Christian Bohr studerade 1904 hemoglobinets bindning till syre under olika förhållanden. När han ritade hemoglobinmättnaden med syre som en funktion av syrepartialtrycket fick han en sigmoidal (eller “S-formad”) kurva. Detta tyder på att ju mer syre är bundet till hemoglobin, desto lättare är det för mer syre att binda – tills alla bindningsställen är mättade. Bohr noterade dessutom att ett ökande koldioxidtryck försköt denna kurva åt höger – dvs. högre koncentrationer av koldioxid gör det svårare för hemoglobin att binda syre. Det sistnämnda fenomenet, tillsammans med observationen att hemoglobins affinitet för syre ökar med stigande pH, är känt som Bohr-effekten.

Originalfigur från Christian Bohr, som visar den sigmoidala ökningen av syrehemoglobin som en funktion av syrepartialtrycket.

En receptormolekyl sägs uppvisa kooperativ bindning om dess bindning till liganden skalar icke-linjärt med ligandkoncentrationen. Kooperativitet kan vara positiv (om bindning av en ligandmolekyl ökar receptorns skenbara affinitet och därmed ökar chansen att en annan ligandmolekyl binder) eller negativ (om bindning av en ligandmolekyl minskar affiniteten och därmed gör det mindre sannolikt att andra ligandmolekyler binder). Den “fraktionella beläggningen” Y ¯ {\displaystyle {\bar {Y}}}

av en receptor med en given ligand definieras som mängden ligandbundna bindningsställen dividerat med den totala mängden ligandbindningsställen: Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}}}={\frac {}{}{}}}}}

Om Y ¯ = 0 {\displaystyle {\bar {Y}}=0}

är proteinet helt obundet, och om Y ¯ = 1 {\displaystyle {\bar {Y}}=1}

är det helt mättat. Om diagrammet för Y ¯ {\displaystyle {\bar {Y}}}

vid jämvikt som funktion av ligandkoncentrationen har en sigmoidal form, vilket Bohr observerade för hemoglobin, tyder detta på positiv kooperativitet. Om så inte är fallet kan man inte uttala sig om kooperativitet enbart genom att titta på denna graf.

Begreppet kooperativ bindning gäller endast för molekyler eller komplex med mer än en ligands bindningsställen. Om det finns flera ligandbindningsställen, men ligandbindning till något av ställena inte påverkar de andra, sägs receptorn vara icke-kooperativ. Samarbetsförmågan kan vara homotrop, om en ligand påverkar bindningen av ligander av samma typ, eller heterotrop, om den påverkar bindningen av andra typer av ligander. När det gäller hemoglobin observerade Bohr homotrop positiv kooperativitet (bindning av syre underlättar bindning av mer syre) och heterotrop negativ kooperativitet (bindning av koldioxid minskar hemoglobins förmåga att binda syre).)

Under hela 1900-talet har olika ramar utvecklats för att beskriva bindningen av en ligand till ett protein med mer än en bindningsplats och de kooperativa effekter som observeras i detta sammanhang.

The Hill equationEdit

Den första beskrivningen av kooperativ bindning till ett protein med flera bindningsplatser utvecklades av A.V. Hill. Med utgångspunkt i observationer av syrebindning till hemoglobin och idén att kooperativitet uppstod genom aggregering av hemoglobinmolekyler som var och en band en syremolekyl, föreslog Hill en fenomenologisk ekvation som sedan dess har fått sitt namn efter honom:

Hillplot av Hillekvationen i rött, med kurvans lutning som Hillkoefficienten och skärningspunkten med x-axeln som ger den skenbara dissociationskonstanten. Den gröna linjen visar den icke-samarbetsvilliga kurvan.

Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {\bar {Y}}={\frac {K\cdot {}^{n}}{1+K\cdot {}^{n}}}={\frac {^{n}}}{K^{*}+^{n}}}={\frac {^{n}}{K_{d}^{n}+^{n}}}}

varvid n {\displaystyle n}

är “Hillkoefficienten”, {\displaystyle }

betecknar ligandkoncentrationen, K {\displaystyle K}

betecknar en skenbar associationskonstant (används i ekvationens ursprungliga form), K ∗ {\displaystyle K^{*}}

är en empirisk dissociationskonstant och K d {\displaystyle K_{d}}

är en mikroskopisk dissociationskonstant (används i moderna former av ekvationen och motsvarar en E C 50 {\displaystyle \mathrm {EC} _{50}}

). Om n < 1 {\displaystyle n<1}

uppvisar systemet negativ kooperativitet, medan kooperativiteten är positiv om n > 1 {\displaystyle n>1}

. Det totala antalet bindningsställen för liganden är en övre gräns för n {\displaystyle n}

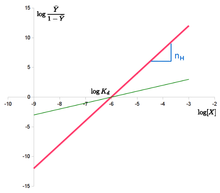
. Hillsekvationen kan linjäriseras som: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log-n\cdot {}\log K_{d}}

The “Hill plot” fås genom att plotta log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}}

mot log {\displaystyle \log}

. När det gäller Hill-ekvationen är det en linje med lutningen n H {\displaystyle n_{H}}

och intercept log ( K d ) {\displaystyle \log(K_{d})}

. Detta innebär att kooperativiteten antas vara fast, dvs. att den inte förändras med mättnaden. Det innebär också att bindningsställena alltid uppvisar samma affinitet, och att kooperativitet inte beror på att affiniteten ökar med ligandkoncentrationen.

Adair-ekvationenRedigera

G.S. Adair upptäckte att Hill-plotten för hemoglobin inte var en rak linje och ställde hypotesen att bindningsaffiniteten inte var en fast term utan beroende av ligandmättnaden. Efter att ha visat att hemoglobin innehöll fyra hemes (och därmed bindningsställen för syre) utgick han från antagandet att fullt mättat hemoglobin bildas i etapper, med mellanformer med en, två eller tre bundna syremolekyler. Bildandet av varje mellanstadium från obundet hemoglobin kan beskrivas med hjälp av en skenbar makroskopisk associationskonstant K i {\displaystyle K_{i}}

. Den resulterande fraktionella beläggningen kan uttryckas som: Y ¯ = 1 4 ⋅ K I + 2 K I I I 2 + 3 K I I I I 3 + 4 K I V 4 1 + K I + K I I I 2 + K I I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, för varje protein med n ligandbindningsställen:

Y ¯ = 1 n K I + 2 K I I I 2 + … + n K n n n 1 + K I + K I I I 2 + … + K n n {\displaystyle {\bar {Y}}={\frac {1}{n}}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

där n betecknar antalet bindningsställen och varje K i {\displaystyle K_{i}}

är en kombinerad associationskonstant som beskriver bindningen av i ligandmolekyler.Genom att kombinera Adairbehandlingen med Hillplotten kommer man fram till den moderna experimentella definitionen av kooperativitet (Hill, 1985, Abeliovich, 2005). Den resulterande Hillkoefficienten, eller rättare sagt lutningen på Hillplotten som beräknas utifrån Adair-ekvationen, kan visas vara förhållandet mellan variansen av bindningsantalet och variansen av bindningsantalet i ett likvärdigt system av icke samverkande bindningsställen. Hillkoefficienten definierar således kooperativitet som ett statistiskt beroende för en bindningsställe av tillståndet hos andra ställen.

Klotz ekvationEdit

Irving Klotz, som arbetade med kalciumbindande proteiner, avvecklade Adairs associationskonstanter genom att ta hänsyn till stegvis bildning av mellanliggande stadier och försökte uttrycka den kooperativa bindningen i termer av elementära processer som styrs av massaktionslagen. I hans ramverk är K 1 {\displaystyle K_{1}}}

den associationskonstant som styr bindningen av den första ligandmolekylen, K 2 {\displaystyle K_{2}}}

den associationskonstant som styr bindningen av den andra ligandmolekylen (när den första redan är bunden) osv. För Y ¯ {\displaystyle {\bar {Y}}}}

ger detta: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {\displaystyle {\bar {Y}}}={\frac {1}{n}}}{\frac {K_{1}+2K_{1}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Det är värt att notera att konstanterna K 1 {\displaystyle K_{1}}

, K 2 {\displaystyle K_{2}}

och så vidare har inget att göra med enskilda bindningsställen. De beskriver hur många bindningsplatser som är upptagna, snarare än vilka. Denna form har den fördelen att kooperativitet lätt känns igen när man betraktar associationskonstanterna. Om alla bindningsställen för ligander är identiska med en mikroskopisk associationskonstant K {\displaystyle K}

, skulle man förvänta sig att K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}}K,\ldots K_{n}={\frac {1}{n}}}K}

(det vill säga K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}}K}

) i frånvaro av samarbete. Vi har positiv kooperativitet om K i {\displaystyle K_{i}}

ligger över dessa förväntade värden för i > 1 {\displaystyle i>1}

.

Klotz-ekvationen (som ibland också kallas Adair-Klotz-ekvationen) används fortfarande ofta i den experimentella litteraturen för att beskriva mätningar av ligandbindning i termer av sekventiella skenbara bindningskonstanter.

Pauling-ekvationRedigera

I mitten av 1900-talet ökade intresset för modeller som inte bara beskrev bindningskurvorna fenomenologiskt, utan som också erbjöd en underliggande biokemisk mekanism. Linus Pauling omtolkade den ekvation som Adair tillhandahöll och antog att hans konstanter var en kombination av bindningskonstanten för liganden ( K { {\displaystyle K}

i ekvationen nedan) och energin som kommer från interaktionen mellan underenheterna i det kooperativa proteinet ( α {\displaystyle \alpha }

nedan). Pauling härledde faktiskt flera ekvationer, beroende på graden av interaktion mellan subenheterna. Baserat på felaktiga antaganden om hemes lokalisering valde han fel ekvation för att beskriva hemoglobins syrebindning, om man antar att underenheterna var arrangerade i en kvadrat. Ekvationen nedan ger ekvationen för en tetraedrisk struktur, vilket skulle vara mer korrekt i fallet med hemoglobin: Y ¯ = K + 3 α K 2 2 2 + 3 α 3 K 3 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 2 + 4 α 3 K 3 3 3 + α 6 K 4 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alpha {}K^{2}^{2}+3\alpha {}^{3}K^{3}^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}{1+4K+6\alpha {}K^{2}^{2}^{2}+4\alpha {}^{3}K^{3}^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}}}

KNF-modellenRedigera

Baserad på resultat som visar att strukturen hos kooperativa proteiner förändrades vid bindning till sin ligand, Daniel Koshland och kollegor förfinade den biokemiska förklaringen till den mekanism som Pauling hade beskrivit. Koshland-Némethy-Filmer-modellen (KNF) utgår från att varje underenhet kan existera i en av två konformationer: aktiv eller inaktiv. Bindning av en ligand till en underenhet skulle leda till en omedelbar konformationsförändring av denna underenhet från den inaktiva till den aktiva konformationen, en mekanism som beskrivs som “induced fit” (inducerad anpassning). Enligt KNF-modellen skulle samverkan uppstå genom interaktioner mellan underenheterna, vars styrka varierar beroende på de inblandade underenheternas relativa konformationer. För en tetraedrisk struktur (de tog även hänsyn till linjära och kvadratiska strukturer) föreslog de följande formel:

Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B B ( K X K t ) 2 + 3 K A B 3 K B B B 3 ( K X K t ) 3 + K B B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Varför K X {\displaystyle K_{X}}

är associationskonstanten för X, K t {\displaystyle K_{t}}

är förhållandet mellan B- och A-tillstånden i frånvaro av ligand (“övergång”), K A B {\displaystyle K_{AB}}

och K B B {\displaystyle K_{BB}}

är de relativa stabiliteterna hos par av angränsande subenheter i förhållande till ett par där båda subenheterna befinner sig i A-tillståndet (Observera att KNF-dokumentet faktiskt presenterar N s {\displaystyle N_{s}}

, antalet ockuperade platser, som här är 4 gånger Y ¯ {\displaystyle {\bar {Y}}}}

).

MWC-modellenRedigera

Monod-Wyman-Changeux-modellens reaktionsschema för ett protein som består av två protomerer. Protomeren kan existera i två tillstånd, vart och ett med olika affinitet för liganden. L är förhållandet mellan tillstånden i frånvaro av ligand, c är förhållandet mellan affiniteterna.

Energidiagram för en Monod-Wyman-Changeux-modell av ett protein som består av två protomerer. Ligandens större affinitet för R-tillståndet innebär att det senare föredraget stabiliseras av bindningen.

Monod-Wyman-Changeux-modellen (MWC) för samordnade allosteriska övergångar gick ett steg längre genom att utforska kooperativitet baserat på termodynamik och tredimensionella konformationer. Den formulerades ursprungligen för oligomeriska proteiner med symmetriskt arrangerade, identiska underenheter som var och en har en ligandbindningsplats. Enligt denna ram kan två (eller fler) interkonvertibla konformationstillstånd hos ett allosteriskt protein samexistera i en termisk jämvikt. Tillstånden – som ofta kallas spända (T) och avslappnade (R) – skiljer sig åt i affinitet för ligandmolekylen. Förhållandet mellan de två tillstånden regleras genom bindning av ligandmolekyler som stabiliserar tillståndet med högre affinitet. Det är viktigt att alla underenheter i en molekyl ändrar tillstånd samtidigt, ett fenomen som kallas “samordnad övergång”.

Den allosteriska isomeriseringskonstanten L beskriver jämvikten mellan de båda tillstånden när ingen ligandmolekyl är bunden: L = {\displaystyle L={\frac {\left}{\left}}}

. Om L är mycket stor finns större delen av proteinet i T-tillståndet i avsaknad av ligand. Om L är liten (nära ett) är R-tillståndet nästan lika populärt som T-tillståndet. Förhållandet mellan dissociationskonstanter för liganden från T- och R-tillstånden beskrivs av konstanten c: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}}{K_{d}^{T}}}}

. Om c = 1 {\displaystyle c=1}

har både R- och T-tillstånd samma affinitet för liganden och liganden påverkar inte isomeriseringen. Värdet på c anger också hur mycket jämvikten mellan T- och R-tillstånden förändras vid bindning av liganden: ju mindre c, desto mer förskjuts jämvikten mot R-tillståndet efter en bindning. Med α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}

, beskrivs fraktionell beläggning som: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Den sigmoida Hillplotten för allosteriska proteiner kan sedan analyseras som en progressiv övergång från T-tillståndet (låg affinitet) till R-tillståndet (hög affinitet) när mättnaden ökar. Hillplottens lutning beror också på mättnaden, med ett maximalt värde vid inflexionspunkten. Skärningarna mellan de två asymptoterna och y-axeln gör det möjligt att bestämma de båda tillståndens affinitet för liganden.

Hillplot för MWC-bindningsfunktionen i rött, för det rena T- och R-tillståndet i grönt. När konformationen skiftar från T till R gör även bindningsfunktionen det. Skärningarna med x-axeln ger den skenbara dissociationskonstanten samt de mikroskopiska dissociationskonstanterna för R- och T-tillstånden.

I proteiner är konformationsförändringar ofta förknippade med aktivitet, eller aktivitet mot specifika mål. Sådan aktivitet är ofta det som är fysiologiskt relevant eller det som mäts experimentellt. Graden av konformationsförändring beskrivs av tillståndsfunktionen R ¯ {\displaystyle {\bar {R}}}

, som anger den fraktion av protein som finns i R {\displaystyle R}}

state. Som energidiagrammet visar är R ¯ {\displaystyle {\bar {R}}}

ökar när fler ligandmolekyler binds. Uttrycket för R ¯ {\displaystyle {\bar {R}}}

är: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}}={\frac {(1+\alpha )^{n}}}{(1+\alpha )^{n}}+L(1+c\alpha )^{n}}}}

En viktig aspekt av MWC-modellen är att kurvorna för Y ¯ {\displaystyle {\bar {Y}}}

och R ¯ {\displaystyle {\bar {R}}}

sammanfaller inte, dvs. fraktionell mättnad är inte en direkt indikator på konformationstillstånd (och därmed på aktivitet). Dessutom kan omfattningen av bindningens och aktiveringens kooperativitet vara mycket olika: ett extremfall är bakteriernas flagellamotor med en Hillkoefficient på 1,7 för bindningen och 10,3 för aktiveringen. Svarets överlinjäritet kallas ibland för ultrakänslighet.

Om ett allosteriskt protein binder till ett mål som också har en högre affinitet för R-tillståndet, stabiliserar målbindningen ytterligare R-tillståndet och ökar därmed ligandens affinitet. Om ett mål å andra sidan föredrar att binda till T-tillståndet kommer målbindning att ha en negativ effekt på ligandens affinitet. Sådana mål kallas allosteriska modulatorer.

Sedan starten har MWC-ramen utvidgats och generaliserats. Variationer har föreslagits, till exempel för att tillgodose proteiner med mer än två tillstånd, proteiner som binder till flera typer av ligander eller flera typer av allosteriska modulatorer och proteiner med icke-identiska underenheter eller ligandbindningsställen.