Työ määritellään energiaksi, jonka lisäät kappaleeseen kohdistamalla voimaa F jollakin matkalla r.

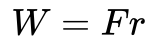
Tämähän voi tarkoittaa esimerkiksi kappaleen nostamista ylöspäin r matkan verran painovoimaa vastaan. Tällöin lisätty energia on potentiaalienergiaa. Tässä tapauksessa haluan kuitenkin näyttää, miten työ liittyy liike-energiaan.

Jos kohdistat kappaleeseen voiman, jotta se liikkuisi nopeammin, kasvatat sen liike-energiaa.

Näytän, miten nämä kaksi liittyvät toisiinsa käyttämällä yhtä aiemmin käsittelemistäni liikeyhtälöistä.

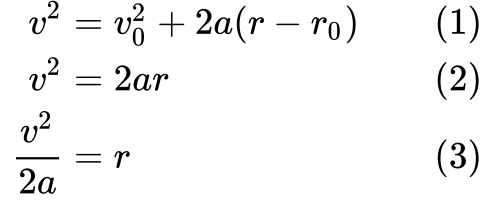
Aloitetaan määritelmästä (1) ja yksinkertaistetaan (2) sitä sanomalla, että alkunopeus v₀ ja kuljettu alkumatka r₀ ovat molemmat nolla.

Viimeiseksi järjestämme (3) yhtälön uudelleen saadaksemme tavan ilmaista r, jotta voimme korvata sen yhtälöllä W = Fr.

Haluamme myös päästä eroon kiihtyvyydestä yhtälöstä, koska liike-energian lauseke ei sisällä sitä. Järjestetään Newtonin toinen laki uudelleen:

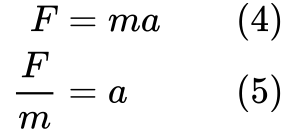
Nyt meillä on palaset, joista voimme johtaa kineettisen energian yhtälön.

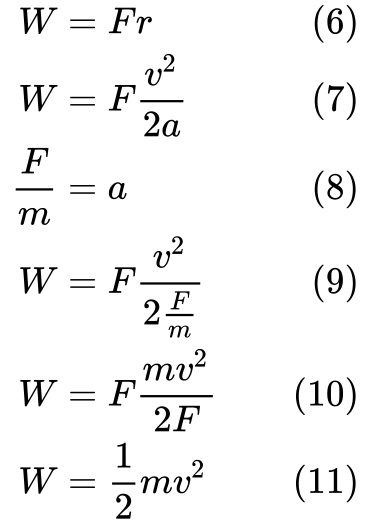
(7) Korvaa r yhtälöllä (3). Sitten voimme korvata a yhtälön (9) kiihtyvyyden määritelmällä yhtälössä (8).

Viimeiseksi (11) näemme, että työ on yhtä kuin liike-energia.

Lukiessani tätä viestiä sattumalta uudestaan läpi huomasin, että lähestymistapani olisi voinut olla paljon yksinkertaisempi.

Jos lähdemme liikkeelle yhtälöstä W = Fv²/2a ja F = ma, niin korvaamme a:n sijasta F:llä suoraan ja saamme sen sijaan arvoksi W = mav²/2a. Silloin a on helppo poistaa ja päädymme tulokseen W = mv²/2.