A munka az az energia, amelyet egy tárgyhoz egy erő F alkalmazásával r bizonyos távolságon keresztül r hozzáadunk.

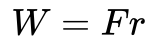
Ez jelentheti pl. egy tárgy felemelését r a gravitáció ellenében. A hozzáadott energia ekkor potenciális energia. Ebben az esetben azonban azt szeretném megmutatni, hogy a munka hogyan függ össze a mozgási energiával.

Ha erőt alkalmazunk egy tárgyra, hogy az gyorsabban mozogjon, akkor növeljük a mozgási energiáját.

A korábban tárgyalt mozgásegyenletek egyikének segítségével megmutatom, hogyan függ össze a kettő.

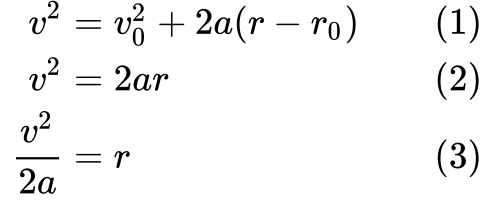
A definícióval (1) kezdjük, majd egyszerűsítjük (2) azt, hogy a kezdeti sebesség v₀ és a megtett kezdeti távolság r₀ egyaránt nulla.

Végül átrendezzük (3) az egyenletet, hogy megkapjuk a r kifejezés módját, így azt be tudjuk helyettesíteni W = Fr-ba.

A gyorsulást is ki akarjuk iktatni az egyenletből, mert a mozgási energia kifejezése nem tartalmazza azt. Rendezzük át Newtons második törvényét:

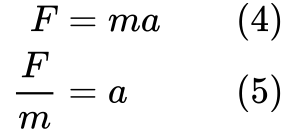
Most megkaptuk a darabokat, hogy levezessük a mozgási energia egyenletét.

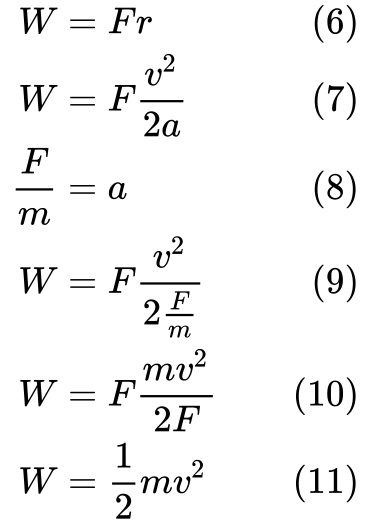
(7) Helyettesítsük a r egyenletet a (3) egyenletével. Ezután a (9) egyenletben lévő a-et helyettesíthetjük a (8) egyenletben lévő gyorsulás definíciójával.

Végül (11) láthatjuk, hogy a munka egyenlő a mozgási energiával.

Mikor véletlenül újra átolvastam ezt a hozzászólást, észrevettem, hogy a megközelítésem sokkal egyszerűbb lehetett volna.

Ha W = Fv²/2a és F = ma-ból indulunk ki, akkor az a helyett közvetlenül F-et helyettesítjük, és W = mav²/2a-t kapunk helyette. Ekkor az a könnyen kiiktatható, és a végeredmény W = mv²/2 lesz.