Il lavoro è definito come l’energia che si aggiunge ad un oggetto applicando una forza F su una certa distanza r.

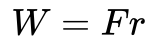
Questo potrebbe significare, ad esempio, sollevare un oggetto per una distanza r contro la gravità. L’energia aggiunta è quindi energia potenziale. Tuttavia in questo caso voglio mostrare come il lavoro sia collegato all’energia cinetica.

Se si applica una forza ad un oggetto, per farlo muovere più velocemente, si aumenta la sua energia cinetica.

Vi mostrerò come le due cose sono collegate usando una delle equazioni del moto che ho trattato prima.

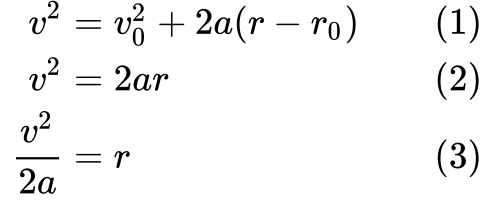
Partiamo dalla definizione (1) e poi la semplifichiamo (2) dicendo che la velocità iniziale v₀ e la distanza iniziale percorsa r₀ sono entrambe zero.

Infine riorganizziamo (3) l’equazione per ottenere un modo di esprimere r, in modo da poterlo sostituire in W = Fr.

Vogliamo anche eliminare l’accelerazione dall’equazione, perché l’espressione dell’energia cinetica non la contiene. Riorganizziamo la seconda legge di Newton:

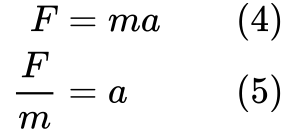
Ora abbiamo i pezzi per ricavare l’equazione dell’energia cinetica.

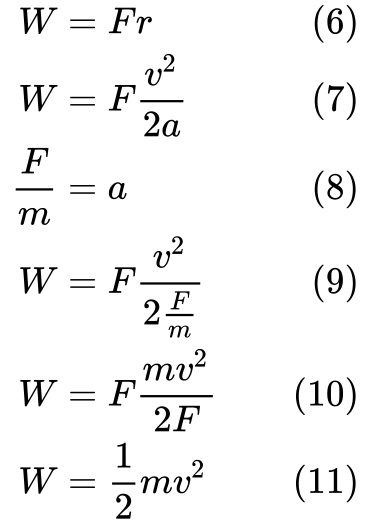
(7) sostituiamo r con l’equazione (3). Poi possiamo sostituire a nell’equazione (9) con la definizione di accelerazione nell’equazione (8).

Infine (11) possiamo vedere che il lavoro è uguale all’energia cinetica.

Leggendo di nuovo questo post per caso ho notato che il mio approccio avrebbe potuto essere molto più semplice.

Se partiamo da W = Fv²/2a e F = ma allora sostituiamo direttamente F al posto di a, e otteniamo W = mav²/2a. Allora a si elimina facilmente e ci ritroviamo con W = mv²/2.