Christian Bohr en het concept van coöperatieve bindingEdit

In 1904 bestudeerde Christian Bohr de binding van hemoglobine aan zuurstof onder verschillende omstandigheden. Toen hij de verzadiging van hemoglobine met zuurstof uitzette als functie van de partiële zuurstofdruk, kreeg hij een sigmoïdale (of “S-vormige”) curve. Dit wijst erop dat hoe meer zuurstof aan hemoglobine gebonden is, hoe gemakkelijker het is om meer zuurstof te binden – totdat alle bindingsplaatsen verzadigd zijn. Bovendien merkte Bohr op dat een toenemende CO2-druk deze curve naar rechts deed verschuiven – d.w.z. hogere concentraties CO2 maken het voor hemoglobine moeilijker om zuurstof te binden. Dit laatste verschijnsel, samen met de waarneming dat de affiniteit van hemoglobine voor zuurstof toeneemt naarmate de pH stijgt, staat bekend als het Bohr-effect.

Originele figuur van Christian Bohr, die de sigmoïdale toename van oxyhemoglobine toont als functie van de partiële zuurstofdruk.

Van een receptormolecuul wordt gezegd dat het coöperatieve binding vertoont als zijn binding aan het ligand niet-lineair schommelt met de ligandconcentratie. Coöperativiteit kan positief zijn (als binding van een ligandmolecuul de schijnbare affiniteit van de receptor verhoogt, en dus de kans op binding van een ander ligandmolecuul vergroot) of negatief (als binding van een ligandmolecuul de affiniteit verlaagt en dus binding van andere ligandmoleculen minder waarschijnlijk maakt). De “fractionele bezettingsgraad” Y ¯ {\displaystyle {Y}}

van een receptor met een bepaald ligand wordt gedefinieerd als de hoeveelheid ligandgebonden bindingsplaatsen gedeeld door de totale hoeveelheid ligandbindingsplaatsen: Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}}={\frac {}{}}}

Als Y ¯ = 0 {\displaystyle {\bar {Y}}=0}

, dan is het eiwit volledig ongebonden, en als Y ¯ = 1 {\displaystyle {\bar {Y}}=1}

, dan is het eiwit volledig verzadigd. Als de plot van Y ¯ {\displaystyle {\bar {Y}}

bij evenwicht als functie van de ligandconcentratie sigmoïdaal van vorm is, zoals waargenomen door Bohr voor hemoglobine, wijst dit op positieve coöperativiteit. Als dit niet het geval is, kan op basis van deze grafiek alleen geen uitspraak worden gedaan over de coöperativiteit.

Het concept van coöperatieve binding geldt alleen voor moleculen of complexen met meer dan één ligandbindingsplaats. Als er meerdere bindingsplaatsen voor liganden zijn, maar binding van een ligand aan een van die plaatsen heeft geen invloed op de andere, wordt gezegd dat de receptor niet coöperatief is. Coöperativiteit kan homotroop zijn, als een ligand de binding van liganden van dezelfde soort beïnvloedt, of heterotroop, als het de binding van andere soorten liganden beïnvloedt. In het geval van hemoglobine constateerde Bohr homotrope positieve coöperativiteit (binding van zuurstof vergemakkelijkt de binding van meer zuurstof) en heterotrope negatieve coöperativiteit (binding van CO2 vermindert de mogelijkheid van hemoglobine om zuurstof te binden.)

In de loop van de 20e eeuw zijn verschillende raamwerken ontwikkeld om de binding van een ligand aan een eiwit met meer dan één bindingsplaats en de coöperatieve effecten die in deze context worden waargenomen, te beschrijven.

De Hill-vergelijkingEdit

De eerste beschrijving van coöperatieve binding aan een eiwit met meerdere plaatsen werd ontwikkeld door A.V. Hill. Op basis van waarnemingen van zuurstofbinding aan hemoglobine en het idee dat coöperativiteit ontstaat door de aggregatie van hemoglobine moleculen, die elk een zuurstofmolecuul binden, stelde Hill een fenomenologische vergelijking voor die sindsdien naar hem is genoemd:

Heuvelplot van de Hill-vergelijking in rood, waarbij de helling van de curve de Hill-coëfficiënt is en het intercept met de x-as de schijnbare dissociatieconstante. De groene lijn geeft de niet-samenwerkende curve.

Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {Y}}={\frac {K\cdot {}^{n}}{1+K\cdot {}^{n}}={\frac {^{n}}{K^{*}+^{n}}={\frac {^{n}}{K_{d}^{n}+^{n}}}}

waar n {\displaystyle n}

de “Heuvelcoëfficiënt” is, {\displaystyle }

de ligandconcentratie, K { {displaystyle K}

de schijnbare associatieconstante (die in de oorspronkelijke vorm van de vergelijking wordt gebruikt), K ∗ {displaystyle K^{*}}

is een empirische dissociatieconstante, en K d {\displaystyle K_{d}}

een microscopische dissociatieconstante (gebruikt in moderne vormen van de vergelijking, en equivalent aan een E C 50 {\displaystyle \mathrm {EC} _{50}}

). Als n < 1 {{\displaystyle n<1}

, vertoont het systeem negatieve coöperativiteit, terwijl de coöperativiteit positief is als n > 1 {\displaystyle n>1}

. Het totale aantal bindingsplaatsen voor liganden is een bovengrens voor n {\displaystyle n}

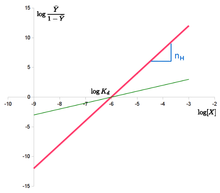
. De Hill vergelijking kan worden gelineariseerd als: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n ⋅ log-n⋅ log K_{d}}

Het “Heuvelplot” wordt verkregen door log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}}}}}1-{\bar {Y}}}}}

tegen log {\displaystyle \log}

. In het geval van de vergelijking van Hill, is het een lijn met helling n H {\displaystyle n_{H}}

en intercept log ( K d ) {Displaystyle \log(K_{d})}

. Dit betekent dat de coöperativiteit wordt verondersteld vast te zijn, d.w.z. dat deze niet verandert naarmate de verzadiging toeneemt. Het betekent ook dat bindingsplaatsen altijd dezelfde affiniteit hebben, en dat de coöperativiteit niet het gevolg is van een affiniteit die toeneemt met de ligandconcentratie.

De vergelijking van AdairEdit

G.S. Adair ontdekte dat de Hill plot voor hemoglobine geen rechte lijn was, en veronderstelde dat de bindingsaffiniteit geen vaste term was, maar afhankelijk van de verzadiging van het ligand. Nadat hij had aangetoond dat hemoglobine vier hemen bevatte (en dus bindingsplaatsen voor zuurstof), ging hij uit van de veronderstelling dat volledig verzadigd hemoglobine in fasen wordt gevormd, met tussenvormen met één, twee, of drie gebonden zuurstofmoleculen. De vorming van elk tussenstadium uit ongebonden hemoglobine kan worden beschreven met behulp van een schijnbare macroscopische associatieconstante K i {\displaystyle K_{i}}

. De resulterende fractionele bezetting kan worden uitgedrukt als: Y ¯ = 1 4 ⋅ K I + 2 K I I 2 + 3 K I I 3 + 4 K I V 4 1 + K I + K I I I 2 + K I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, voor elk eiwit met n ligandbindingsplaatsen:

Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {\displaystyle {Y}}={\frac {1}{n}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

waarbij n staat voor het aantal bindingsplaatsen en elke K i {{i}}

een gecombineerde associatieconstante is, die de binding van i ligandmoleculen beschrijft.Door de Adair-behandeling te combineren met de Hill-plot, komt men tot de moderne experimentele definitie van coöperativiteit (Hill, 1985, Abeliovich, 2005). De resulterende Hill coëfficiënt, of correcter de helling van de Hill plot zoals berekend uit de Adair Vergelijking, kan worden aangetoond als de verhouding tussen de variantie van het bindingsgetal en de variantie van het bindingsgetal in een equivalent systeem van niet-interagerende bindingsplaatsen. Aldus definieert de Hill coëfficiënt de coöperativiteit als een statistische afhankelijkheid van één bindingsplaats van de toestand van andere plaats(en).

De Klotz-vergelijkingEdit

Werkend aan calciumbindende eiwitten, deconvolueerde Irving Klotz Adair’s associatieconstanten door stapsgewijze vorming van de tussenstadia te beschouwen, en probeerde de coöperatieve binding uit te drukken in termen van elementaire processen beheerst door de massa actiewet. In zijn kader is K 1 {\displaystyle K_{1}}

de associatieconstante voor de binding van het eerste ligandmolecuul, K 2 {\displaystyle K_{2}}

de associatieconstante voor de binding van het tweede ligandmolecuul (als het eerste al gebonden is) enz. Voor Y ¯ {\displaystyle {Y}}

, geeft dit: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {\displaystyle {Y}}={\frac {1}{n}}{\frac {K_{1}+2K_{1}K_{2}^{2}+\ldots +n\left(K_{1}K_{2} K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Het is de moeite waard op te merken dat de constanten K 1 {\displaystyle K_{1}}

, K 2 {\displaystyle K_{2}}

enzovoort hebben geen betrekking op afzonderlijke bindingsplaatsen. Ze beschrijven hoeveel bindingsplaatsen er bezet zijn, niet welke. Deze vorm heeft het voordeel dat coöperativiteit gemakkelijk wordt herkend wanneer de associatieconstanten worden bekeken. Als alle ligandbindingsplaatsen identiek zijn met een microscopische associatieconstante K {Displaystyle K}

, zou men verwachten dat K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {Displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}

(dat is K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}K}

) in de afwezigheid van coöperativiteit. We hebben positieve coöperativiteit als K i {\displaystyle K_{i}}

boven deze verwachte waarden ligt voor i > 1 {\displaystyle i>1}

.

De Klotz-vergelijking (die soms ook de Adair-Klotz-vergelijking wordt genoemd) wordt in de experimentele literatuur nog vaak gebruikt om metingen van ligandbinding te beschrijven in termen van opeenvolgende schijnbare bindingsconstanten.

Pauling-vergelijkingEdit

In het midden van de 20e eeuw was er een toenemende belangstelling voor modellen die niet alleen de bindingskrommen fenomenologisch zouden beschrijven, maar ook een onderliggend biochemisch mechanisme zouden bieden. Linus Pauling herinterpreteerde de vergelijking van Adair, waarbij hij ervan uitging dat zijn constanten de combinatie waren van de bindingsconstante voor het ligand ( K {{displaystyle K}

in de vergelijking hieronder) en energie afkomstig van de interactie tussen subeenheden van het samenwerkende eiwit ( α {{displaystyle \alpha }

hieronder). Pauling leidde in feite verschillende vergelijkingen af, afhankelijk van de mate van interactie tussen de subeenheden. Op basis van verkeerde veronderstellingen over de lokalisatie van hemes koos hij voor de verkeerde vergelijking om de zuurstofbinding door hemoglobine te beschrijven, ervan uitgaande dat de subeenheden in een vierkant waren gerangschikt. De vergelijking hieronder geeft de vergelijking voor een tetrahedrale structuur, die nauwkeuriger zou zijn in het geval van hemoglobine: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 + α 6 K 4 4 {\displaystyle {\bar {Y}}={\frac {K+3 {}K^{2}^{2}+3}+3}+4}} {}^{6}K^{4}^{4}}}{1+4K+6}} {}K^{2}^{2}+4}+4}} {}^{3}K^{3}^{3}+3}+4}} {}^{6}K^{4}^{4}}}}}

Het KNF-modelEdit

Gebaseerd op resultaten die aantoonden dat de structuur van coöperatieve eiwitten veranderde bij binding aan hun ligand, verfijnden Daniel Koshland en collega’s de biochemische verklaring van het door Pauling beschreven mechanisme. Het Koshland-Némethy-Filmer (KNF) model gaat ervan uit dat elke subeenheid kan bestaan in één van twee conformaties: actief of inactief. Ligandbinding aan één subeenheid zou een onmiddellijke conformatieverandering van die subeenheid van de inactieve naar de actieve conformatie teweegbrengen, een mechanisme dat wordt beschreven als “geïnduceerde fit”. Volgens het KNF-model zou de coöperativiteit het gevolg zijn van interacties tussen de subeenheden, waarvan de sterkte varieert naar gelang van de relatieve conformatie van de betrokken subeenheden. Voor een tetraëdrische structuur (zij namen ook lineaire en vierkante structuren in aanmerking) stelden zij de volgende formule voor

Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B ( K X K t ) 2 + 3 K A B 3 K B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B ( K X K t ) 2 + 4 K A B 3 K B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\displaybar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Waarbij K X {K_{X}}

de associatieconstante voor X is, K t {\displaystyle K_{t}}

is de verhouding tussen de B- en de A-toestand bij afwezigheid van ligand (“overgang”), K A B {Displaystyle K_{AB}}

en K B B {\displaystyle K_{BB}}

zijn de relatieve stabiliteiten van paren van aangrenzende subeenheden ten opzichte van een paar waarbij beide subeenheden in de A-toestand zijn (Merk op dat het KNF-paper in feite N s {{BB}}

, het aantal bezette plaatsen, dat hier 4 maal Y ¯ {{s}}

).

Het MWC-modelEdit

Monod-Wyman-Changeux modelreactieschema van een eiwit dat uit twee protomeren bestaat. Het protomeer kan in twee toestanden bestaan, elk met een verschillende affiniteit voor het ligand. L is de verhouding van de toestanden bij afwezigheid van het ligand, c is de verhouding van de affiniteiten.

Energiediagram van een Monod-Wyman-Changeux-model van een eiwit dat uit twee protomeren bestaat. De grotere affiniteit van het ligand voor de R-toestand betekent dat deze laatste bij voorkeur wordt gestabiliseerd door de binding.

Het Monod-Wyman-Changeux (MWC) model voor gecoördineerde allosterische overgangen ging een stap verder door de coöperativiteit te onderzoeken op basis van thermodynamica en driedimensionale conformaties. Het werd oorspronkelijk geformuleerd voor oligomere eiwitten met symmetrisch gerangschikte, identieke subeenheden, die elk één ligandbindingsplaats hebben. Volgens dit raamwerk bestaan twee (of meer) interconverteerbare conformatie toestanden van een allosterisch eiwit naast elkaar in een thermisch evenwicht. De toestanden – vaak gespannen (T) en ontspannen (R) genoemd – verschillen in affiniteit voor het ligandmolecuul. De verhouding tussen de twee toestanden wordt geregeld door de binding van ligandmoleculen die de toestand met de hogere affiniteit stabiliseren. Belangrijk is dat alle subeenheden van een molecuul tegelijkertijd van toestand veranderen, een fenomeen dat bekend staat als “gecoördineerde overgang”.

De allosterische isomerisatieconstante L beschrijft het evenwicht tussen beide toestanden wanneer er geen ligandmolecuul gebonden is: L = {Displaystyle L={\frac {\left}{\left}}}

. Als L erg groot is, bevindt het grootste deel van het eiwit zich in de T-toestand in afwezigheid van ligand. Als L klein is (dicht bij 1), is de R-toestand bijna net zo bevolkt als de T-toestand. De verhouding van de dissociatieconstanten voor het ligand uit de T en R toestanden wordt beschreven door de constante c: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Als c = 1 {Displaystyle c=1}

, hebben zowel de R- als de T-toestand dezelfde affiniteit voor het ligand en heeft het ligand geen invloed op de isomerisatie. De waarde van c geeft ook aan in hoeverre het evenwicht tussen de T- en R-toestand verandert bij binding van het ligand: hoe kleiner c, hoe meer het evenwicht verschuift naar de R-toestand na één binding. Met α = K d R {{\displaystyle \alpha ={K_{d}^{R}}}}

, wordt de fractionele bezetting beschreven als: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {{Y}}={\frac {{}}^{n-1}+Lc(1+c\alpha )^{n-1}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

De sigmoïde Hill-plot van allosterische eiwitten kan dan worden geanalyseerd als een progressieve overgang van de T-toestand (lage affiniteit) naar de R-toestand (hoge affiniteit) naarmate de saturatie toeneemt. De helling van de Hill plot hangt ook af van de verzadiging, met een maximumwaarde bij het inflexiepunt. De intervallen tussen de twee asymptoten en de y-as maken het mogelijk de affiniteit van beide toestanden voor het ligand te bepalen.

Heuvelplot van de bindingsfunctie van MWC in rood, van de zuivere T- en R-toestand in groen. Naarmate de conformatie verschuift van T naar R, doet de bindingsfunctie dat ook. De intercepts met de x-as geven de schijnbare dissociatieconstante en de microscopische dissociatieconstanten van de R en T toestanden.

In eiwitten wordt conformationele verandering vaak geassocieerd met activiteit, of activiteit ten opzichte van specifieke doelen. Deze activiteit is vaak wat fysiologisch relevant is of wat experimenteel wordt gemeten. De mate van conformatieverandering wordt beschreven door de toestandsfunctie R ¯ {\displaystyle {{R}}}

, die de fractie aangeeft van eiwit dat aanwezig is in de R¯ {\displaystyle R}

state. Zoals het energiediagram laat zien, is R¯ {\displaystyle R}}

toenemen naarmate er meer ligandmoleculen binden. De uitdrukking voor R ¯ {\bar {R}}

is: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {{\displaystyle {\bar {R}}}={\frac {(1+alpha )^{n}}{(1+alpha )^{n}+L(1+c\alpha )^{n}}}}

Een cruciaal aspect van het MWC-model is dat de krommen voor Y ¯ {displaystyle {{R}}}

en R¯ {\displaystyle {\bar {R}}}

vallen niet samen, d.w.z. dat de fractionele verzadiging geen directe indicator is van de conformatie (en dus van de activiteit). Bovendien kunnen de mate van coöperativiteit van binding en coöperativiteit van activering zeer verschillend zijn: een extreem geval is dat van de flagellamotor van de bacterie met een Hill coëfficiënt van 1,7 voor de binding en 10,3 voor de activering. De supra-lineariteit van de respons wordt ook wel ultrasensitiviteit genoemd.

Als een allosterisch eiwit bindt aan een doelwit dat ook een hogere affiniteit heeft voor de R-toestand, dan stabiliseert de doelwitbinding de R-toestand verder, waardoor de affiniteit van het ligand toeneemt. Als, aan de andere kant, een doelwit bij voorkeur bindt aan de T toestand, dan zal doelwitbinding een negatief effect hebben op de ligandaffiniteit. Dergelijke targets worden allosterische modulatoren genoemd.

Sinds het begin is het MWC raamwerk uitgebreid en veralgemeend. Variaties zijn voorgesteld, bijvoorbeeld voor eiwitten met meer dan twee toestanden, eiwitten die binden aan verschillende soorten liganden of verschillende soorten allosterische modulatoren en eiwitten met niet-identieke subeenheden of ligand-bindende sites.