Wykresy w Pythonie

Origins of Graph Theory

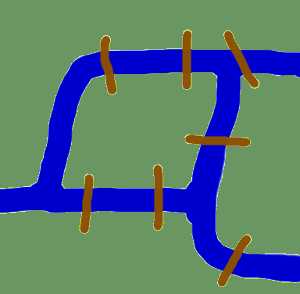Zanim zaczniemy od rzeczywistych implementacji grafów w Pythonie i zanim zaczniemy wprowadzać moduły Pythona zajmujące się grafami, chcemy poświęcić się początkom teorii grafów.
Początki cofają nas w czasie do Królewca w XVIII wieku. Königsberg był wtedy miastem w Prusach. Przez miasto przepływała rzeka Pregel, tworząc dwie wyspy. Miasto i wyspy były połączone siedmioma mostami, jak pokazano na rysunku. Mieszkańców miasta nurtowało pytanie, czy można odbyć spacer po mieście, odwiedzając każdą jego część i przechodząc przez każdy most tylko raz? Każdy most musi być pokonany w całości, tzn. nie można przejść połowy mostu, a następnie zawrócić i przejść drugą połowę z drugiej strony. Spacer nie musi zaczynać się i kończyć w tym samym miejscu. Leonhard Euler rozwiązał ten problem w 1735 roku, udowadniając, że nie jest to możliwe. Odkrył, że wybór trasy wewnątrz każdego obszaru lądowego jest nieistotny i że jedyną rzeczą, która ma znaczenie, jest kolejność (lub sekwencja), w której mosty są przekraczane. Sformułował abstrakcję problemu, eliminując zbędne fakty i koncentrując się na obszarach lądowych i łączących je mostach. W ten sposób stworzył podstawy teorii grafów. Jeśli postrzegamy “obszar lądowy” jako wierzchołek, a każdy most jako krawędź, to “zredukowaliśmy” problem do grafu.

Wprowadzenie do teorii grafów przy użyciu Pythona

Zanim rozpoczniemy naszą rozprawę na temat możliwych reprezentacji grafów w Pythonie, chcemy przedstawić kilka ogólnych definicji grafów i ich składników.
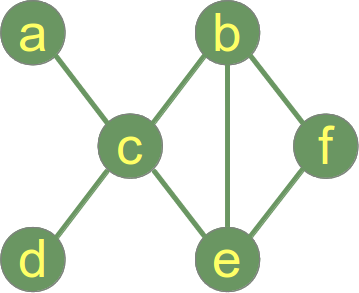
“Graf “1 w matematyce i informatyce składa się z “węzłów”, zwanych też “wierzchołkami”.Węzły mogą być ze sobą połączone lub nie. Na naszej ilustracji, – która jest obrazowym przedstawieniem grafu, – węzeł “a” jest połączony z węzłem “c”, ale “a” nie jest połączony z “b”. Linia łącząca dwa węzły nazywana jest krawędzią. Jeśli krawędzie między węzłami są nieskierowane, to graf nazywamy grafem nieskierowanym. Jeśli krawędź jest skierowana z jednego wierzchołka (węzła) do drugiego, graf nazywamy grafem skierowanym. Krawędź skierowana nazywana jest łukiem.
Chociaż grafy mogą wyglądać bardzo teoretycznie, wiele praktycznych problemów może być reprezentowanych przez grafy. Są one często używane do modelowania problemów lub sytuacji w fizyce, biologii, psychologii, a przede wszystkim w informatyce. W informatyce, grafy są używane do reprezentowania sieci komunikacyjnych, organizacji danych, urządzeń obliczeniowych, przepływu obliczeń,

W tym ostatnim przypadku, grafy są używane do reprezentowania organizacji danych, jak system plików w systemie operacyjnym, lub sieci komunikacyjnych. Struktura linków na stronach internetowych może być również postrzegana jako graf, tzn. graf skierowany, ponieważ link jest skierowaną krawędzią lub łukiem.
Python nie ma wbudowanego typu danych ani klasy dla grafów, ale łatwo jest je zaimplementować w Pythonie. Jeden typ danych jest idealny do reprezentowania grafów w Pythonie, tj. słowniki. Graf na naszej ilustracji może być zaimplementowany w następujący sposób:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Klucze powyższego słownika są węzłami naszego grafu. Odpowiadające im wartości to listy z węzłami, które są połączone krawędzią. Nie ma prostszego i bardziej eleganckiego sposobu na reprezentację grafu.
Krawędź może być postrzegana jako 2-tuple z węzłami jako elementami, tj. (“a”, “b”)
Funkcja generująca listę wszystkich krawędzi:Ten kod generuje następujące dane wyjściowe, jeśli jest połączony z wcześniej zdefiniowanym słownikiem grafu:

 $ python3 graph_simple.py 

Jak widzimy, nie ma żadnej krawędzi zawierającej węzeł “f”. “f” jest izolowanym węzłem naszego grafu.
Następująca funkcja Pythona oblicza izolowane węzły danego grafu:Jeśli wywołamy tę funkcję z naszym grafem, zwrócona zostanie lista zawierająca “f”:

Graphs as a Python Class

Zanim przejdziemy do pisania funkcji dla grafów, mamy za sobą pierwsze podejście do implementacji klasy grafów w Pythonie. Jeśli spojrzysz na poniższy listing naszej klasy, możesz zobaczyć w metodzie __init__, że używamy słownika “self.__graph_dict” do przechowywania wierzchołków i odpowiadających im sąsiednich wierzchołków.
Jeśli uruchomisz ten moduł autonomicznie, otrzymasz następujący wynik:

Ścieżki w grafach

Chcemy teraz znaleźć najkrótszą ścieżkę z jednego węzła do innego węzła. Zanim przejdziemy do kodu Pythona dla tego problemu, będziemy musieli przedstawić kilka formalnych definicji.
Sąsiadujące wierzchołki:
Dwa wierzchołki są sąsiadujące, gdy oba są zderzone ze wspólną krawędzią.
Ścieżka w grafie nieskierowanym:
Ścieżka w grafie nieskierowanym to ciąg wierzchołków P = ( v1, v2, …., vn ) ∈ V x V x … x V taki, że vi jest przyległy do v{i+1} dla 1 ≤ i < n. Taka ścieżka P jest nazywana ścieżką długości n od v1 do vn.
Ścieżka prosta:
Ścieżkę bez powtarzających się wierzchołków nazywamy ścieżką prostą.
Przykład:
(a, c, e) jest ścieżką prostą w naszym grafie, podobnie jak (a,c,e,b). (a,c,e,b,c,d) jest ścieżką, ale nie jest prostą ścieżką, ponieważ węzeł c pojawia się dwa razy.

Następująca metoda znajduje ścieżkę od wierzchołka początkowego do wierzchołka końcowego:Jeśli zapiszemy naszą klasę grafu zawierającą metodę find_path jako “graphs.py”, możemy sprawdzić sposób działania naszej funkcji find_path:Wynik poprzedniego programu wygląda tak:
Metoda find_all_paths znajduje wszystkie ścieżki pomiędzy wierzchołkiem początkowym a wierzchołkiem końcowym:Zmieniliśmy nieco nasz przykładowy graf, dodając krawędzie od “a” do “f” oraz od “f” do “d”, aby przetestować wcześniej zdefiniowaną metodę:Wynik wygląda następująco:

Stopień

Stopień wierzchołka v w grafie to liczba łączących go krawędzi, przy czym pętle liczone są podwójnie. Stopień wierzchołka v jest oznaczany jako deg(v). Maksymalny stopień grafu G, oznaczany przez Δ(G), i minimalny stopień grafu, oznaczany przez δ(G), to maksymalny i minimalny stopień jego wierzchołków.
W grafie po prawej stronie maksymalny stopień to 5 w wierzchołku c, a minimalny to 0, czyli wierzchołek izolowany f.
Jeśli wszystkie stopnie w grafie są takie same, to graf jest grafem regularnym.W grafie regularnym wszystkie stopnie są takie same, a więc możemy mówić o stopniu grafu.
Wzór na sumę stopni (Handshaking lemma):
∑v &w; Vdeg(v) = 2 |E|
To oznacza, że suma stopni wszystkich wierzchołków jest równa liczbie krawędzi pomnożonej przez 2.Możemy z tego wywnioskować, że liczba wierzchołków o stopniu nieparzystym musi być parzysta. Stwierdzenie to znane jest jako lemat uścisku dłoni. Nazwa “handshaking lemma” pochodzi od popularnego problemu matematycznego: w dowolnej grupie osób liczba osób, które podały rękę nieparzystej liczbie innych osób z tej grupy jest parzysta.
Następująca metoda oblicza stopień wierzchołka:
Następująca metoda oblicza listę zawierającą izolowane wierzchołki grafu:Metody delta i Delta mogą być użyte do obliczenia odpowiednio minimalnego i maksymalnego stopnia wierzchołka:

Sekwencja stopni

Sekwencja stopni grafu nieskierowanego jest zdefiniowana jako sekwencja stopni jego wierzchołków w porządku nierosnącym.
Następująca metoda zwraca tuple z sekwencją stopni grafu instancji:
Sekwencja stopni naszego przykładowego grafu jest następującym ciągiem liczb całkowitych: (5,2,1,1,1,0).
Isomorficzne grafy mają taką samą sekwencję stopni. Jednak dwa grafy o tej samej sekwencji stopni nie muszą być izomorficzne.
Pojawia się pytanie, czy dana sekwencja stopni może być zrealizowana przez graf asymetryczny. Twierdzenie Erdösa-Gallai’a mówi, że nierosnący ciąg n liczb di (dlai = 1, …, n) jest ciągiem stopni grafu prostego wtedy i tylko wtedy, gdy suma tego ciągu jest parzysta i spełniony jest następujący warunek:

Implementacja twierdzenia Erdösa-Gallai’a

Nasza klasa grafów – patrz niżej – zawiera metodę “erdoes_gallai”, która decyduje, czy ciąg spełnia twierdzenie Erdösa-Gallai’a. W pierwszej kolejności sprawdzamy, czy suma tego ciągu jest parzysta. Najpierw sprawdzamy, czy suma elementów ciągu jest nieparzysta. Jeżeli tak, to funkcja zwraca False, ponieważ twierdzenie Erdösa-Gallai’a nie może być już spełnione. Następnie za pomocą statycznej metody is_degree_sequence sprawdzamy, czy wejściowa sekwencja jest sekwencją stopnia, tzn. czy jej elementy są nierosnące. Jest to trochę zbędne, ponieważ dane wejściowe mają być sekwencją stopni, więc możesz zrezygnować z tego sprawdzania dla zwiększenia wydajności. Teraz sprawdzamy w ciele drugiej instrukcji if, czy nierówność twierdzenia jest spełniona:
Wersja bez zbędnego testu kolejności stopni:

Gęstość grafu

Gęstość grafu definiujemy jako stosunek liczby krawędzi danego grafu, do całkowitej liczby krawędzi, jaką graf mógłby mieć. Innymi słowy: Mierzy, jak blisko dany graf jest do grafu kompletnego.
Maksymalna gęstość wynosi 1, jeśli graf jest kompletny. Jest to oczywiste, ponieważ maksymalna liczba krawędzi w grafie zależy od wierzchołków i można ją obliczyć w następujący sposób:
max. liczba krawędzi = ½ * |V| * ( |V| – 1 ).
Z drugiej strony minimalna gęstość wynosi 0, jeśli graf nie ma krawędzi, czyli jest grafem izolowanym.
Dla prostych grafów nieskierowanych gęstość grafu definiuje się jako: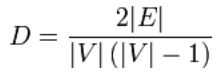

Graf gęsty to taki, w którym liczba krawędzi jest bliska maksymalnej liczbie krawędzi. Graf, który ma tylko kilka krawędzi, nazywamy grafem rzadkim. Definicja dla tych dwóch pojęć nie jest zbyt ostra, tzn. nie ma najmniejszego górnego ograniczenia (supremum) dla grafu rzadkiego i największego dolnego ograniczenia (infimum) dla zdefiniowania grafu gęstego.
Precyzyjna notacja matematyczna używa notacji dużego O:
Sparse Graph:
Graf gęsty:
Graf gęsty to graf G = (V, E), w którym |E| = Θ(|V|2).
“density” to metoda naszej klasy służąca do obliczania gęstości grafu:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Możemy przetestować tę metodę za pomocą następującego skryptu. Graf pełny ma gęstość 1, a izolowany 0, co widać po wynikach poprzedniego skryptu testowego:

$ python test_density.py 0.4666666666671.00.0

Grafy połączone

O grafie mówimy, że jest połączony, jeśli każda para wierzchołków w grafie jest połączona. Przykładowy graf po prawej stronie jest grafem połączonym.

Czy graf jest połączony można określić za pomocą prostego algorytmu:

1. Wybierz dowolny węzeł x grafu G jako punkt początkowy
2. Określ zbiór A wszystkich węzłów, do których można dotrzeć z x.
3. Jeśli A jest równe zbiorowi węzłów G, graf jest połączony; w przeciwnym razie jest rozłączny.

Zaimplementowaliśmy metodę is_connected do sprawdzania, czy graf jest grafem połączonym. Nie kładziemy nacisku na wydajność, ale na czytelność.
Jeśli dodasz tę metodę do naszej klasy grafu, możemy ją przetestować za pomocą poniższego skryptu. Zakładając, że zapiszesz klasę grafu jako graph2.py:
Składnik połączony to maksymalny połączony podgraf grafu G. Każdy wierzchołek należy do dokładnie jednego składnika połączonego, podobnie jak każda krawędź.

Dystans i średnica grafu

Dystans “dist” między dwoma wierzchołkami w grafie to długość najkrótszej ścieżki między tymi wierzchołkami. Przy obliczaniu odległości nie są dozwolone żadne backtracki, objazdy ani pętle.
W naszym przykładowym grafie po prawej stronie, odległość między wierzchołkiem a i wierzchołkiem f wynosi 3, tzn. dist(a,f) = 3, ponieważ najkrótsza droga prowadzi przez wierzchołki c i e (lub c i b alternatywnie).
Ekscentryczność wierzchołka s grafu g to maksymalna odległość od każdego innego wierzchołka grafu:
e(s) = max( { dist(s,v) | v ∈ V })
(V to zbiór wszystkich wierzchołków g)
Średnicę d grafu definiuje się jako maksymalną ekscentryczność dowolnego wierzchołka w grafie. Oznacza to, że średnica jest długością najkrótszej ścieżki pomiędzy najbardziej oddalonymi od siebie węzłami. Aby wyznaczyć średnicę grafu, należy najpierw znaleźć najkrótszą ścieżkę pomiędzy każdą parą wierzchołków. Największa długość dowolnej z tych ścieżek jest średnicą grafu.
W naszym przykładowym grafie możemy bezpośrednio zobaczyć, że średnica wynosi 3, ponieważ minimalna długość między a i f wynosi 3 i nie ma innej pary wierzchołków z dłuższą ścieżką.
Następująca metoda implementuje algorytm do obliczania średnicy. Średnicę naszego przykładowego grafu możemy obliczyć za pomocą następującego skryptu, zakładając ponownie, że nasza kompletna klasa grafu jest zapisana jako graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Wyświetli ona wartość 3.

Kompletna klasa grafu Pythona

W poniższym kodzie Pythona znajduje się kompletny moduł klasy Pythona ze wszystkimi omówionymi metodami:graph2.py

Drzewo / Las

Drzewo jest grafem nieskierowanym, który nie zawiera cykli. Oznacza to, że dowolne dwa wierzchołki grafu są połączone dokładnie jedną prostą ścieżką.
Las jest rozłączną unią drzew. W przeciwieństwie do lasów w przyrodzie, las w teorii grafów może składać się z pojedynczego drzewa!
Graf z jednym wierzchołkiem i bez krawędzi jest drzewem (i lasem).
Przykład drzewa: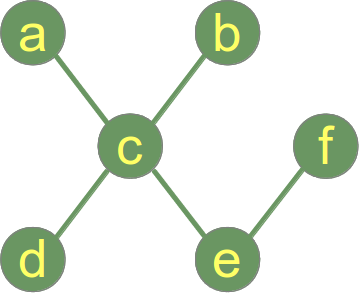

Poprzedni przykład przedstawia graf, który jest drzewem i lasem, natomiast poniższy rysunek przedstawia graf, który składa się z dwóch drzew, tzn.czyli graf jest lasem, ale nie jest drzewem:

Przegląd lasów:

Z jednym wierzchołkiem:

Wykresy leśne z dwoma wierzchołkami:

Grafy leśne z trzema wierzchołkami:

Drzewo rozpinające

Drzewo rozpinające T połączonego, nieskierowanego grafu G to podgraf G’ grafu G, który jest drzewem,a G’ zawiera wszystkie wierzchołki i podzbiór krawędzi G. G’ zawiera wszystkie krawędzie G, jeśli G jest grafem drzewiastym. Nieformalnie, drzewo rozpinające G to wybór krawędzi G, które tworzą drzewo rozpinające każdy wierzchołek. Oznacza to, że każdy wierzchołek leży w tym drzewie, ale nie zawiera ono cykli (ani pętli).
Przykład:
W pełni połączony graf: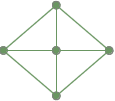

Dwa drzewa rozpinające z poprzedniego w pełni połączonego grafu: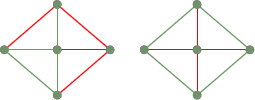

Gra Hamiltonowska

Ścieżka Hamiltonowska to ścieżka w grafie niekierowanym lub skierowanym, która odwiedza każdy wierzchołek dokładnie raz. Cykl Hamiltona (lub obwód) to ścieżka Hamiltona, która jest cyklem.
Uwaga dla informatyków: Ogólnie, nie jest możliwe określenie, czy takie ścieżki lub cykle istnieją w arbitralnych grafach, ponieważ problem ścieżek Hamiltona został udowodniony jako NP-complete.
Nazwa pochodzi od Williama Rowana Hamiltona, który wymyślił tak zwaną “grę icosian”, lub zagadkę Hamiltona, która polega na znalezieniu cyklu Hamiltona w grafie krawędziowym dodekaedru. Hamilton rozwiązał ten problem używając rachunku icosian, struktury algebraicznej opartej na korzeniach jedności z wieloma podobieństwami do kwaternionów, które również wymyślił.

Kompletny listing klasy Graph

Możemy przetestować klasę Graph za pomocą następującego programu:Jeśli uruchomimy ten program, otrzymamy następujące dane wyjściowe:
Przypisy:
1 Grafów badanych w teorii grafów (i w tym rozdziale naszego samouczka Pythona) nie należy mylić z grafami funkcji
2 Singleton to zbiór, który zawiera dokładnie jeden element.
Uznanie:
Narayana Chikkam, nchikkam(at)gmail(dot)com, wskazał błąd indeksu w metodzie “erdoes_gallai”. Dziękuję ci bardzo, Narayana!
.