Arystoteles (Ἀριστοτέλης) 384-322 p.n.e. był greckim filozofem i naukowcem urodzonym w mieście Stagira, w klasycznej Grecji.

W wieku 17 lat wstąpił do Akademii Platońskiej w Atenach i pozostał tam do trzydziestego siódmego roku życia (ok. 347 p.n.e.)

Jego pisma obejmują wiele tematów – w tym fizykę, biologię, zoologię, logikę, etykę, poezję, teatr, muzykę, językoznawstwo i politykę. Stanowią one pierwszy kompleksowy system filozofii zachodniej.

• excerpted and adapted from Aristotle. (2016, October 20). Wikipedia, The Free Encyclopedia.

Arystoteles wyznaczył 3 prawa ruchu, oparte na obserwacjach (ale nie na eksperymencie)

* obiekty w niebiosach (sfera niebieska) poruszają się ruchem okrężnym,bez żadnej zewnętrznej siły zmuszającej je do tego.obiekty na Ziemi (sfera ziemska) poruszają się po liniach prostych, chyba że zostaną zmuszone do ruchu okrężnego.

Co z pchaniem i ciągnięciem?

Ruch naturalny a nienaturalny

Co by się więc stało, gdyby armata wystrzeliła kulę armatnią? Arystoteles przypuszczał, że poruszałaby się ona po linii prostej (z powodu nienaturalnej siły), a następnie spadłaby prosto w dół (z powodu innej, naturalnej siły).)

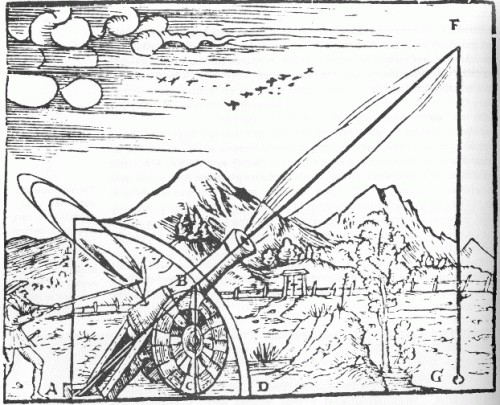
Dla Arystotelesa, raz “gwałtowny ruch” (od ludzi) wygasł, naturalny ruch przejmuje kontrolę, a następnie kula armatnia spada do swojego naturalnego miejsca, ziemi.

Jednakże, jak pokazał Galielo w 1500 roku, pogląd Arystotelesa wcale nie jest poprawny. Każdy, kto obserwuje łucznika wystrzeliwującego strzałę w powietrze i uważnie obserwuje, zobaczyłby, że tak się nie dzieje.

Ruch pionowy powoli maleje, osiąga zero (w punkcie szczytowym), a następnie wzrasta w przeciwnym kierunku (w dół).

Siły niebieskie vs siły ziemskie

Wierzyło się, że obiekty ziemskie (lądowe) mają oddzielny zestaw praw ruchu. Ziemskie obiekty rzekomo zawsze przestawałyby się poruszać, z własnej woli, same z siebie.

* obiekty naturalnie poruszają się tylko po liniach prostych.* aby obiekty miały ruch okrężny, potrzebna jest jakaś zewnętrzna siła, utrzymująca je w ruchu okrężnym

Arystoteles nigdy nie przeprowadzał eksperymentów, więc był bardzo ograniczony w tym, co mógł zaobserwować.W epoce średniowiecza Galileusz (i inni) przeprowadzał kontrolowane eksperymenty.Wyniki tych eksperymentów były analizowane za pomocą matematyki.

Galileusz nauczył się umiejętności krytycznego myślenia od swojego ojca, Vincenza

a. Gdy kulka toczy się w dół, porusza się z grawitacją ziemską, a jej prędkość wzrasta.

c. Gdy piłka toczy się po równej płaszczyźnie, nie porusza się ani z grawitacją, ani przeciw niej.

b. W miarę zmniejszania kąta nachylenia w górę, piłka toczy się na większą odległość, zanim osiągnie swoją początkową wysokość.

Wniosek Galileusza został poparty inną linią rozumowania.

Inclined Plane – Galileo’s Battle for the Heavens PBS NOVA

Rolling balls, cylinders and tubes down inclined plane: Moment bezwładności

Coś specjalnego: Brachistochrone – krzywa najszybszego opadania. I tautochron – krzywa, dla której czas potrzebny obiektowi ślizgającemu się bez tarcia w jednorodnej grawitacji do jego najniższego punktu jest niezależny od punktu początkowego.

Prawa ruchu Arystotelesa.

Wyciąg z wykładu profesora Michaela Fowlera, U. Va. Physics, 9/3/2008

http://galileoandeinstein.physics.virginia.edu/lectures/aristot2.html

To, co Arystoteles osiągnął w tych latach w Atenach, to rozpoczęcie szkoły zorganizowanych dociekań naukowych na skalę znacznie przekraczającą wszystko, co było wcześniej. Po raz pierwszy jasno określił, czym jest wiedza naukowa i dlaczego należy jej szukać. Innymi słowy, własnymi rękami stworzył naukę jako zbiorowe, zorganizowane przedsięwzięcie, którym jest dzisiaj. Akademia Platona miała odpowiednik uniwersyteckiego wydziału matematyki, Arystoteles miał pierwszy wydział naukowy, naprawdę doskonały w biologii, ale, jak zobaczymy, trochę słaby w fizyce.

Po Arystotelesie nie było porównywalnego profesjonalnego przedsięwzięcia naukowego przez ponad 2000 lat, a jego praca była takiej jakości, że została zaakceptowana przez wszystkich i od dawna była częścią oficjalnej ortodoksji Kościoła chrześcijańskiego 2000 lat później. To było niefortunne, bo kiedy Galileusz zakwestionował niektóre z twierdzeń dotyczących prostej fizyki, szybko znalazł się w poważnych tarapatach z Kościołem.
Metoda badawcza Arystotelesa:

określenie tematu

rozważenie związanych z nim trudności poprzez przegląd ogólnie przyjętych poglądów na dany temat oraz sugestii wcześniejszych pisarzy

przedstawienie własnych argumentów i rozwiązań

Takim schematem posługują się współczesne prace badawcze, Arystoteles ustanawiał standardowe, profesjonalne podejście do badań naukowych.

Arystoteles często obalał argumenty przeciwnika pokazując, że prowadzą one do absurdalnego wniosku, nazywa się to reductio ad absurdum (sprowadzanie czegoś do absurdu). Jak zobaczymy później, Galileusz użył dokładnie tego rodzaju argumentu przeciwko samemu Arystotelesowi, ku wielkiej irytacji arystotelików 2,000 lat po Arystotelesie.

W przeciwieństwie do Platona, który uważał, że jedyną wartościową nauką jest kontemplacja abstrakcyjnych form, Arystoteles praktykował szczegółową obserwację i sekcję roślin i zwierząt, aby spróbować zrozumieć, jak każdy z nich pasował do wielkiego planu natury, oraz znaczenie różnych organów zwierząt.

Niezbędne jest uświadomienie sobie, że świat, który Arystoteles widział wokół siebie w codziennym życiu, bardzo różnił się od tego, który widzimy dzisiaj. Każde współczesne dziecko od urodzenia widzi poruszające się samochody i samoloty, i szybko przekonuje się, że te rzeczy nie są żywe, tak jak ludzie i zwierzęta. W przeciwieństwie do tego, większość ruchu widzianego w czwartym wieku Grecji to byli ludzie, zwierzęta i ptaki, wszystkie bardzo żywe. Ten ruch miał jakiś cel, zwierzę poruszało się do miejsca, w którym wolałoby być, z jakiegoś powodu, więc ruch był kierowany przez wolę zwierzęcia.

Dla Arystotelesa ten ruch spełniał zatem “naturę” zwierzęcia, tak jak jego naturalny wzrost spełniał naturę zwierzęcia.

Aby wyjaśnić ruch rzeczy oczywiście nie żywych, takich jak kamień upuszczony z ręki, Arystoteles rozszerzył pojęcie “natury” czegoś na materię nieożywioną. Zasugerował, że ruch takich nieożywionych przedmiotów można zrozumieć postulując, że elementy mają tendencję do poszukiwania swego naturalnego miejsca w porządku rzeczy:

Tak więc ziemia porusza się w dół najmocniej,
woda też płynie w dół, ale nie tak mocno, gdyż kamień spadnie przez wodę.
W przeciwieństwie do tego powietrze porusza się w górę (bąbelki w wodzie),
a ogień porusza się w górę najmocniej ze wszystkich, ponieważ strzela w górę przez powietrze.

Ta ogólna teoria poruszania się elementów musi być oczywiście rozwinięta, gdy zastosuje się ją do rzeczywistych materiałów, które są mieszaninami elementów. Doszedłby do wniosku, że drewno ma w sobie zarówno ziemię, jak i powietrze, ponieważ nie tonie w wodzie.

Ruch naturalny i ruch gwałtowny

Rzeczy poruszają się również dlatego, że są popychane. Naturalną tendencją kamienia, pozostawionego samemu sobie i bez podparcia, jest upadek, ale możemy go podnieść, a nawet rzucić w powietrze.

Arystoteles nazwał taki wymuszony ruch “ruchem gwałtownym” w przeciwieństwie do ruchu naturalnego.

Termin “gwałtowny” oznacza po prostu, że jakaś zewnętrzna siła jest do niego przyłożona.

Arystoteles był pierwszym, który pomyślał ilościowo o prędkościach związanych z tymi ruchami. Wysunął dwa twierdzenia ilościowe o tym, jak rzeczy spadają (ruch naturalny):

Cięższe rzeczy spadają szybciej, a prędkość jest proporcjonalna do ciężaru.

Prędkość spadania danego obiektu zależy odwrotnie od gęstości ośrodka, przez który spada.

Więc, na przykład, to samo ciało będzie spadać dwa razy szybciej przez ośrodek o połowie gęstości.

Zauważ, że te zasady mają pewną elegancję, pociągającą prostotę ilościową. A jeśli upuścimy kamień i kartkę papieru, to jasne jest, że cięższa rzecz spada szybciej, a kamień spadający przez wodę jest zdecydowanie spowalniany przez wodę, więc reguły te na początku wydają się wiarygodne.

Zaskakujące jest to, że w świetle żmudnych obserwacji tak wielu rzeczy Arystoteles nie sprawdził tych reguł w żaden poważny sposób.

Nie zajęłoby dużo czasu, aby dowiedzieć się na przykład, czy połowa cegły spada z połową prędkości całej cegły. Oczywiście, nie było to coś, co uważał za ważne.

Z drugiego twierdzenia powyżej wywnioskował, że próżnia nie może istnieć, ponieważ gdyby tak było, to skoro ma zerową gęstość, wszystkie ciała spadałyby przez nią z nieskończoną prędkością, co jest oczywistym nonsensem.

W przypadku ruchu gwałtownego Arystoteles stwierdził, że prędkość poruszającego się obiektu jest wprost proporcjonalna do przyłożonej siły.

To oznacza po pierwsze, że jeśli przestaniesz pchać, obiekt przestanie się poruszać.

Z pewnością brzmi to jak rozsądna zasada dla, powiedzmy,
pchania pudełka z książkami po dywanie lub wołu ciągnącego pług przez pole.

(Ten intuicyjnie pociągający obraz nie bierze jednak pod uwagę
dużej siły tarcia między pudełkiem a dywanem.
Gdybyś umieścił pudełko na sankach i pchał je po lodzie,
nie zatrzymałoby się, kiedy przestałbyś je pchać.
Wieki później Galileusz zdał sobie sprawę ze znaczenia tarcia w takich sytuacjach.)

Standardy nauczania

2016 Massachusetts Science and Technology/Engineering Curriculum Framework
HS-PS2-1. Analizować dane w celu poparcia twierdzenia, że drugie prawo ruchu Newtona jest
modelem matematycznym opisującym zmianę ruchu (przyspieszenie) obiektów, na które
działa siła netto.

HS-PS2-10(MA). Use free-body force diagrams, algebraic expressions, and Newton’s laws of motion to predict changes to velocity and acceleration for an object moving in one dimension in various situations

Massachusetts History and Social Science Curriculum Framework

Korzenie zachodniej cywilizacji: Starożytna Grecja, C. 800-300 BCE.
7.34 Opisać cele i funkcje rozwoju greckich instytucji, takich jak liceum, gimnazjum i Biblioteka Aleksandryjska, oraz zidentyfikować główne osiągnięcia starożytnych Greków.

WHI.33 Podsumować, jak rewolucja naukowa i metoda naukowa doprowadziły do nowych teorii wszechświata i opisać osiągnięcia czołowych postaci rewolucji naukowej, w tym Bacona, Kopernika, Kartezjusza, Galileusza, Keplera i
Newtona.

A FRAMEWORK FOR K-12 SCIENCE EDUCATION: Practices, Crosscutting Concepts, and Core Ideas
PS2.A: FORCES AND MOTION
Jak można przewidzieć ciągły ruch obiektu, zmiany w ruchu lub stabilność?

Interakcje obiektu z innym obiektem mogą być wyjaśnione i przewidziane przy użyciu koncepcji sił, które mogą spowodować zmianę w ruchu jednego lub obu oddziałujących obiektów… W makroskali, ruch obiektu podlegającego siłom jest regulowany przez drugie prawo ruchu Newtona… Zrozumienie sił między obiektami jest ważne dla opisania jak zmieniają się ich ruchy, jak również dla przewidywania stabilności lub niestabilności w systemach w każdej skali.

.