Test Kołmogorova-Smirnova
Test K-S jest testem dobroci dopasowania używanym do oceny jednorodności zbioru rozkładów danych. Został on zaprojektowany w odpowiedzi na niedoskonałości testu chi-squared, który daje precyzyjne wyniki tylko dla dyskretnych, podzielonych na grupy rozkładów. Test K-S ma tę zaletę, że nie zakłada podziału na grupy porównywanych zbiorów danych, co eliminuje arbitralność i utratę informacji, które towarzyszą procesowi wyboru grupy.
W statystyce, test K-S jest przyjętym testem do pomiaru różnic między ciągłymi zestawami danych (rozkłady danych bez binowania), które są funkcją jednej zmiennej. Ta miara różnicy, statystyka K-S, jest zdefiniowana jako maksymalna wartość bezwzględnej różnicy między dwoma funkcjami rozkładu kumulatywnego. Jednostronny test K-S jest używany do porównania zbioru danych ze znaną funkcją rozkładu skumulowanego, podczas gdy dwustronny test K-S porównuje dwa różne zbiory danych. Każdy zestaw danych daje inną funkcję rozkładu skumulowanego, a jej znaczenie polega na jej związku z rozkładem prawdopodobieństwa, z którego dany zestaw danych został wylosowany: funkcja rozkładu prawdopodobieństwa dla pojedynczej zmiennej niezależnej ∗ jest funkcją, która przypisuje prawdopodobieństwo każdej wartości ∗. Prawdopodobieństwo przyjęte przez konkretną wartość \(x_{i}} jest wartością funkcji rozkładu prawdopodobieństwa przy \(x_{i}} i jest oznaczane jako \(P(x_{i}})\).Funkcja rozkładu skumulowanego jest definiowana jako funkcja określająca frakcję punktów danych znajdujących się na lewo od danej wartości \(x_{i}}, \(P(x <x_{i}})\); przedstawia ona prawdopodobieństwo, że \(x_{i}} jest mniejsze lub równe określonej wartości \(x_{i}}).
Tak więc, dla porównania dwóch różnych funkcji rozkładu skumulowanego \(S_{N1}(x)\) i \(S_{N2}(x)\), statystyka K-S wynosi
D = max|S_N1(x) – S_N2(x)|
gdzie \(S_{N}(x)\) jest funkcją rozkładu skumulowanego rozkładu prawdopodobieństwa, z którego wylosowano zbiór danych zawierający \(N) zdarzeń. Jeśli uporządkowane zdarzenia są zlokalizowane w punktach danych \(x_{i}), gdzie \(i = 1, \), to
S_N(x_i) = (i-N)/N
gdzie tablica danych \(x_i) jest posortowana w porządku rosnącym. Jest to funkcja krokowa, która zwiększa się o \(1/N\) przy wartości każdego uporządkowanego punktu danych.
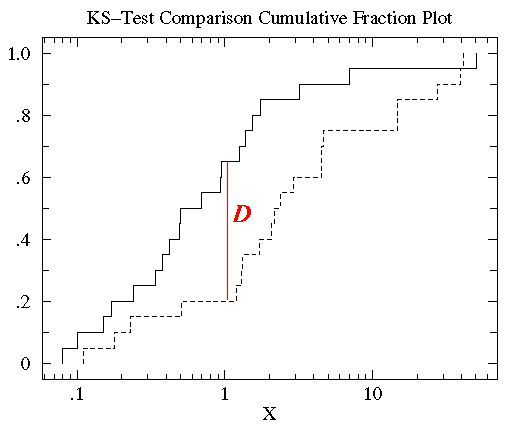
Kirkman, T.W. (1996) Statistists to Use.
http://www.physics.csbsju.edu/stats/
Dla naszych celów, dwa porównywane rozkłady to zmierzony rozkład czasów przybycia, oraz skumulowana frakcja na upływający przedział czasu. Jeśli hipoteza zerowa (brak zmienności) jest prawdziwa, to otrzymujemy 50% zdarzeń w 50% upływającego czasu, a statystyka powinna rozkładać się zgodnie z rozkładem Kołmogorowa dla wielu realizacji rozkładu czasów przybycia. Prawdopodobieństwo zwrócone przez test jest więc \(p_{KS} = 1 – \), gdzie \(\) jest prawdopodobieństwem (zgodnie z rozkładem Kołmogorowa), że wartość \(D\) jest większa lub równa zmierzonej wartości. Mała wartość \(p_{KS}) wskazuje zatem na zgodność z hipotezą zerową, natomiast duża wartość \(p_{KS}) wskazuje, że odstęp czasu między zdarzeniami nie jest stały, a zatem można wnioskować o zmienności.