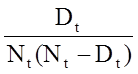Istnieje kilka różnych sposobów oszacowania funkcji przeżycia lub krzywej przeżycia. Istnieje wiele popularnych metod parametrycznych, które są używane do modelowania danych przeżycia, a różnią się one pod względem założeń, które są dokonywane na temat rozkładu czasów przeżycia w populacji. Niektóre popularne rozkłady obejmują rozkład wykładniczy, Weibulla, Gompertza i logarytmiczno-normalny.2 Być może najbardziej popularny jest rozkład wykładniczy, który zakłada, że prawdopodobieństwo doznania przez uczestnika zdarzenia będącego przedmiotem zainteresowania jest niezależne od tego, jak długo osoba ta była wolna od zdarzeń. Inne rozkłady przyjmują różne założenia dotyczące prawdopodobieństwa wystąpienia zdarzenia u danej osoby (tzn. może ono wzrastać, maleć lub zmieniać się w czasie). Więcej szczegółów na temat parametrycznych metod analizy przeżycia można znaleźć w pracach Hosmer i Lemeshow oraz Lee i Wang1,3.

Skupiamy się tutaj na dwóch metodach nieparametrycznych, które nie przyjmują żadnych założeń dotyczących tego, jak prawdopodobieństwo wystąpienia zdarzenia u danej osoby zmienia się w czasie. Używając metod nieparametrycznych, szacujemy i wykreślamy rozkład przeżycia lub krzywą przeżycia. Krzywe przeżycia są często wykreślane jako funkcje krokowe, jak pokazano na poniższym rysunku. Czas jest pokazany na osi X, a przeżywalność (odsetek osób zagrożonych) na osi Y. Należy zauważyć, że odsetek uczestników, którzy przeżyli, nie zawsze reprezentuje odsetek, którzy żyją (co zakłada, że wynikiem zainteresowania jest śmierć). “Przeżycie” może również odnosić się do odsetka, który jest wolny od innego zdarzenia wynikowego (np. odsetek wolny od MI lub choroby sercowo-naczyniowej), lub może również reprezentować odsetek, który nie doświadcza zdrowego wyniku (np. remisja raka).

Funkcja przeżycia

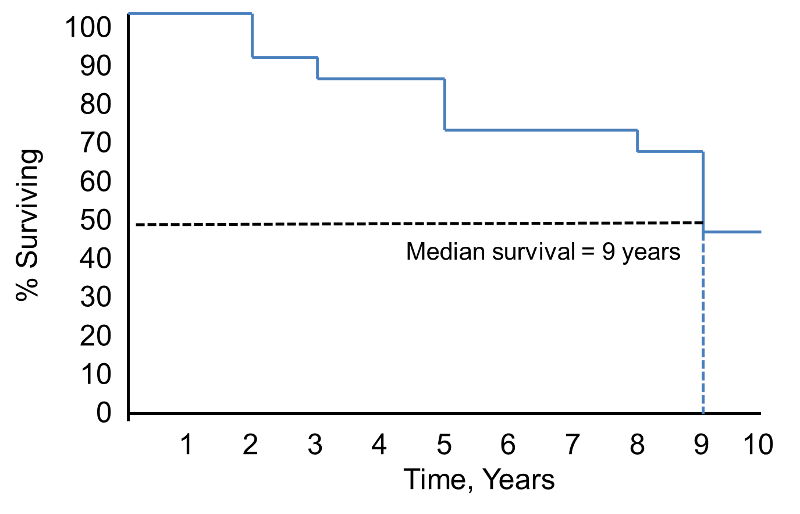
Zauważ, że prawdopodobieństwo przeżycia wynosi 100% przez 2 lata, a następnie spada do 90%. Mediana przeżycia wynosi 9 lat (tzn. 50% populacji przeżywa 9 lat; patrz linie przerywane).

Przykład:

Rozważmy małe prospektywne badanie kohortowe zaprojektowane do badania czasu do śmierci. W badaniu bierze udział 20 uczestników w wieku 65 lat i starszych; są oni włączani do badania w ciągu 5 lat i obserwowani przez okres do 24 lat, aż do śmierci, zakończenia badania lub rezygnacji z badania (lost to follow-up). Dane przedstawiono poniżej. W badaniu odnotowano 6 zgonów i 3 uczestników z pełną obserwacją (tj. 24 lata). Pozostałych 11 ma mniej niż 24 lata obserwacji z powodu późnego zgłoszenia się do badania lub utraty danych.

.

Participant Identification Number	Year of Death	Year Ostatniego Kontaktu
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Tabela życia (Actuarial Table)

Jednym ze sposobów podsumowania doświadczeń uczestników jest tabela życia, lub tabeli aktuarialnej. Tabele trwania życia są często wykorzystywane w branży ubezpieczeniowej do szacowania oczekiwanej długości życia i ustalania składek. Skupiamy się na szczególnym rodzaju tabeli trwania życia używanej powszechnie w analizie biostatystycznej, zwanej kohortową tabelą trwania życia lub tabelą dalszego trwania życia. Tabela dalszego trwania życia podsumowuje doświadczenia uczestników we wcześniej zdefiniowanym okresie obserwacji w badaniu kohortowym lub w badaniu klinicznym do czasu wystąpienia interesującego ich zdarzenia lub zakończenia badania, w zależności od tego, co nastąpi wcześniej.

Aby skonstruować tabelę dalszego trwania życia, najpierw organizujemy czasy obserwacji w równe odstępy. W powyższej tabeli maksymalny czas obserwacji wynosi 24 lata i uwzględniamy 5-letnie przedziały czasowe (0-4, 5-9, 10-14, 15-19 i 20-24 lata). Sumujemy liczbę uczestników, którzy żyją na początku każdego przedziału, liczbę, którzy umierają, oraz liczbę, która jest cenzurowana w każdym przedziale.

Interwał w latach	Liczba osób żyjących na początku interwału	Liczba zgonów podczas interwału	Liczba osób cenzurowanych
0-.4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

W naszej analizie tabeli życia stosujemy następującą notację. Najpierw definiujemy notację, a następnie wykorzystujemy ją do skonstruowania tabeli trwania życia.

• Nt = liczba uczestników, którzy są wolni od zdarzeń i uznani za zagrożonych w przedziale t (np, w tym przykładzie liczba żyjących, ponieważ naszym wynikiem zainteresowania jest śmierć)
• Dt = liczba uczestników, którzy umierają (lub doznają zdarzenia będącego przedmiotem zainteresowania) w przedziale t
• Ct = liczba uczestników, którzy są cenzurowani w przedziale t Nt* = średnia liczba uczestników zagrożonych w przedziale t
• Nt* = średnia liczba uczestników zagrożonych w przedziale t [Przy konstruowaniu aktuarialnych tablic trwania życia często przyjmuje się następujące założenia: Po pierwsze, zakłada się, że zdarzenia będące przedmiotem zainteresowania (np. zgony) występują na końcu przedziału, a zdarzenia cenzurowane występują jednolicie (lub równomiernie) w całym przedziale. Dlatego często dokonuje się korekty Nt, aby odzwierciedlić średnią liczbę uczestników narażonych na ryzyko podczas przedziału, Nt*, którą oblicza się w następujący sposób: Nt* =Nt-Ct/2 (tzn, odejmujemy połowę cenzurowanych zdarzeń).
• qt = proporcja umierających (lub cierpiących z powodu zdarzenia) podczas przedziału t, qt = Dt/Nt*
• pt = proporcja przeżywających (pozostających wolnymi od zdarzeń) przedział t, pt = 1-qt
• St, proporcja przeżywających (lub pozostających wolnymi od zdarzeń) w przeszłości przedziału t; jest to czasami nazywane skumulowanym prawdopodobieństwem przeżycia i jest obliczane w następujący sposób: Po pierwsze, proporcja uczestników przeżywających w czasie przeszłym 0 (czas rozpoczęcia badania) jest określona jako S0 = 1 (wszyscy uczestnicy żyjący lub wolni od zdarzeń w czasie zerowym lub na początku badania). Proporcję przeżywających po każdym kolejnym przedziale oblicza się przy użyciu zasad prawdopodobieństwa warunkowego wprowadzonych w module Prawdopodobieństwo. W szczególności, prawdopodobieństwo, że uczestnik przeżyje po przedziale 1 wynosi S1 = p1. Prawdopodobieństwo, że uczestnik przetrwa do końca przedziału 2 oznacza, że musiał on przeżyć obok przedziału 1 i przez przedział 2: S2 = P(przetrwać do końca przedziału 2) = P(przetrwać do końca przedziału 2)*P(przetrwać do końca przedziału 1), czyli S2 = p2*S1. Ogólnie, St+1 = pt+1*St.

Format tabeli dalszego trwania życia jest przedstawiony poniżej.

Dla pierwszego przedziału, 0-4 lata: W chwili 0, początku pierwszego przedziału (0-4 lata), żyje lub jest zagrożonych 20 uczestników. Dwóch uczestników umiera w tym przedziale, a 1 jest cenzurowany. Stosujemy poprawkę na liczbę uczestników cenzurowanych w tym przedziale, aby otrzymać Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Obliczenia dla pozostałych kolumn są przedstawione w tabeli. Prawdopodobieństwo, że uczestnik przeżyje ponad 4 lata lub ponad pierwszy przedział (używając górnej granicy przedziału do określenia czasu) wynosi S4 = p4 = 0,897.

Dla drugiego przedziału, 5-9 lat: Liczba zagrożonych to liczba zagrożonych w poprzednim przedziale (0-4 lata) pomniejszona o tych, którzy umierają i są cenzurowani (tj. Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). Prawdopodobieństwo, że uczestnik przeżyje powyżej 9 lat wynosi S9 = p9*S4 = 0,937*0,897 = 0,840.

Interwał w latach	Liczba osób zagrożonych podczas interwału, Nt	Średnia liczba osób zagrożonych podczas interwału, Nt*	Number of Deaths During Interval, Dt	Lost to Follow-Up, Ct	Proportion Dying During Interval, qt	Among Those at Risk, Proportion Surviving Interval, pt	Prawdopodobieństwo przeżycia St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

Pełną tabelę dalszego życia przedstawiono poniżej.

Interval in Years	Number At Risk During Interval, Nt	Average Number At Risk During Interval, Nt*	Number of Deaths During Interval, Dt	Lost to Follow-Up, Ct	Proportion Dying During Interval, qt	Among Those at Risk, Proportion Surviving Interval, pt	Survival Probability St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Tabela ta wykorzystuje metodę aktuarialną do konstrukcji tabeli dalszego trwania życia, w której czas podzielony jest na równe odstępy.

Podejście Kaplana-Meiera (Product Limit)

Kwestią związaną z przedstawionym powyżej podejściem tabeli trwania życia jest to, że prawdopodobieństwa przeżycia mogą się zmieniać w zależności od tego, jak przedziały są zorganizowane, szczególnie przy małych próbach. Podejście Kaplana-Meiera, zwane również podejściem limitu produktu, jest popularnym podejściem, które rozwiązuje ten problem poprzez ponowne oszacowanie prawdopodobieństwa przeżycia za każdym razem, gdy wystąpi zdarzenie.

Właściwe zastosowanie podejścia Kaplana-Meiera opiera się na założeniu, że cenzurowanie jest niezależne od prawdopodobieństwa rozwoju interesującego nas zdarzenia oraz że prawdopodobieństwa przeżycia są porównywalne u uczestników, którzy są rekrutowani wcześnie i później do badania. Przy porównywaniu kilku grup ważne jest również, aby te założenia były spełnione w każdej grupie porównawczej i aby na przykład cenzurowanie nie było bardziej prawdopodobne w jednej grupie niż w innej.

W poniższej tabeli wykorzystano metodę Kaplana-Meiera do przedstawienia tych samych danych, które zostały przedstawione powyżej przy użyciu metody tablic trwania życia. Zauważ, że zaczynamy tabelę od Czasu=0 i Prawdopodobieństwa przeżycia = 1. W czasie=0 (punkt wyjściowy lub początek badania) wszyscy uczestnicy są zagrożeni, a prawdopodobieństwo przeżycia wynosi 1 (lub 100%). Przy zastosowaniu metody Kaplana-Meiera prawdopodobieństwo przeżycia jest obliczane przy użyciu St+1 = St*((Nt+1-Dt+1)/Nt+1). Zauważ, że obliczenia przy użyciu metody Kaplana-Meiera są podobne do tych przy użyciu metody aktuarialnej tabeli trwania życia. Główna różnica polega na przedziałach czasowych, tzn. przy podejściu z aktuarialną tablicą trwania życia rozważamy jednakowo odległe przedziały, podczas gdy przy podejściu Kaplana-Meiera używamy czasów obserwowanych zdarzeń i czasów cenzurowania. Obliczenia prawdopodobieństw przeżycia są szczegółowo opisane w kilku pierwszych wierszach tabeli.

Tabela przeżycia przy użyciu metody Kaplana-Meiera

.

Czas, Years	Liczba osób zagrożonych Nt	Liczba zgonów Dt	Liczba ocenzurowana Ct	Prawdopodobieństwo przeżycia St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20				1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3		3	0.507

Przy dużych zbiorach danych obliczenia te są żmudne. Jednakże, analizy te mogą być generowane przez programy do obliczeń statystycznych, takie jak SAS. Excel może być również użyty do obliczenia prawdopodobieństwa przeżycia, gdy dane są uporządkowane według czasu i podsumowane są liczby zdarzeń i czasy cenzurowane.

Z tabeli przeżycia możemy wygenerować krzywą przeżycia Kaplana-Meiera.

Krzywa przeżycia Kaplana-Meiera dla powyższych danych

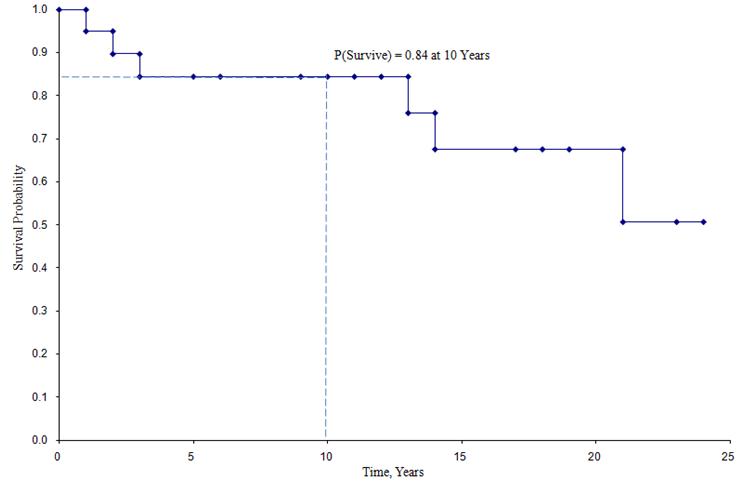
W krzywej przeżycia pokazanej powyżej, symbole reprezentują każdy czas zdarzenia, albo śmierć lub czas cenzurowany. Na podstawie krzywej przeżycia możemy również oszacować prawdopodobieństwo, że uczestnik przeżyje ponad 10 lat, lokalizując 10 lat na osi X i odczytując w górę i w górę do osi Y. Proporcja uczestników, którzy przeżyli 10 lat wynosi 84%, a proporcja uczestników, którzy przeżyli 20 lat wynosi 68%. Mediana przeżycia jest szacowana przez zlokalizowanie 0.5 na osi Y i czytanie w górę i w dół do osi X. Mediana przeżycia wynosi w przybliżeniu 23 lata.

Błędy standardowe i przedziały ufności oszacowań prawdopodobieństwa przeżycia

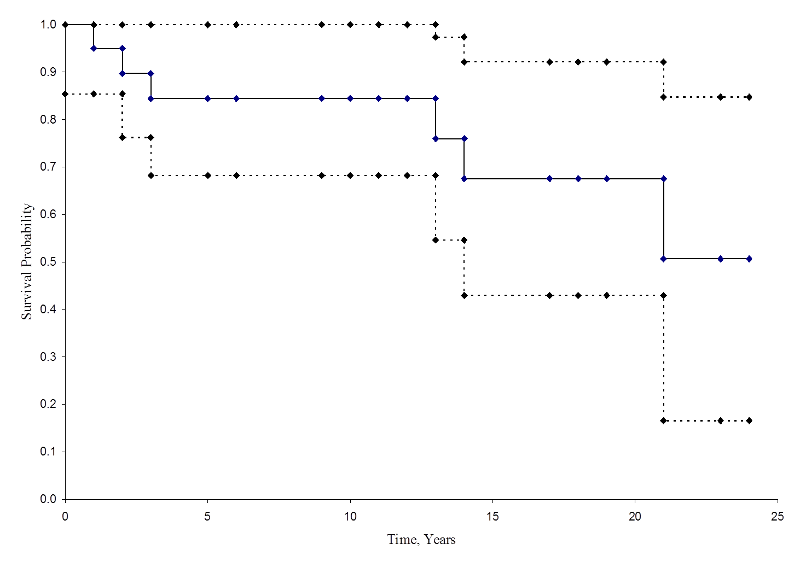
Te oszacowania prawdopodobieństwa przeżycia w określonym czasie i mediany czasu przeżycia są punktowymi oszacowaniami i powinny być interpretowane jako takie. Istnieją wzory do produkcji błędów standardowych i przedziałów ufności oszacowań prawdopodobieństwa przeżycia, które mogą być generowane z wieloma statystycznymi pakietami obliczeniowymi. Popularna formuła do oszacowania błędu standardowego oszacowań przeżycia jest nazywana formułą Greenwoods5 i jest następująca:

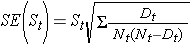
Wielkość 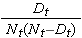jest sumowana dla liczb zagrożonych (Nt) i liczb zgonów (Dt) występujących przez czas zainteresowania (tj. kumulatywnie, przez wszystkie czasy przed czasem zainteresowania, patrz przykład w tabeli poniżej). Błędy standardowe są obliczane dla oszacowań przeżycia dla danych w poniższej tabeli. Proszę zauważyć, że ostatnia kolumna pokazuje wielkość 1.96*SE(St), która jest marginesem błędu i jest używana do obliczania szacunków 95% przedziału ufności (tj. St ± 1.96 x SE(St)).

Błędy standardowe oszacowań przeżycia

Czas, Years	Number at Risk Nt	Number of Deaths Dt	Survival Prawdopodobieństwo St				1.96*SE (St)
0	20		1		.
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0.000	0.118	0.174	0.341

Na poniższym rysunku podsumowano szacunki i przedziały ufności. Krzywa przeżycia Kaplana-Meiera jest przedstawiona jako linia ciągła, a 95% przedziały ufności są przedstawione jako linie przerywane.

Krzywa przeżycia Kaplana-Meiera z przedziałami ufności

Krzywe skumulowanej zachorowalności

Niektórzy badacze wolą generować krzywe skumulowanej zachorowalności, w przeciwieństwie do krzywych przeżycia, które pokazują skumulowane prawdopodobieństwo doświadczenia zdarzenia będącego przedmiotem zainteresowania. Skumulowana częstość występowania, lub skumulowane prawdopodobieństwo niepowodzenia, jest obliczane jako 1-St i może być łatwo obliczone z tabeli życia przy użyciu metody Kaplana-Meiera. Skumulowane prawdopodobieństwa awarii dla powyższego przykładu przedstawiono w poniższej tabeli.

Tablica życia ze skumulowanymi prawdopodobieństwami awarii

.

Czas, Years	Number at Risk Nt	Number of Deaths Dt	Number Censored Ct	Prawdopodobieństwo przeżycia St	Prawdopodobieństwo porażki 1-St
0	20			1	1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0,493

Poniższa rycina przedstawia skumulowaną częstość występowania zgonów dla uczestników włączonych do opisanego powyżej badania.

Krzywa skumulowanej częstości występowania

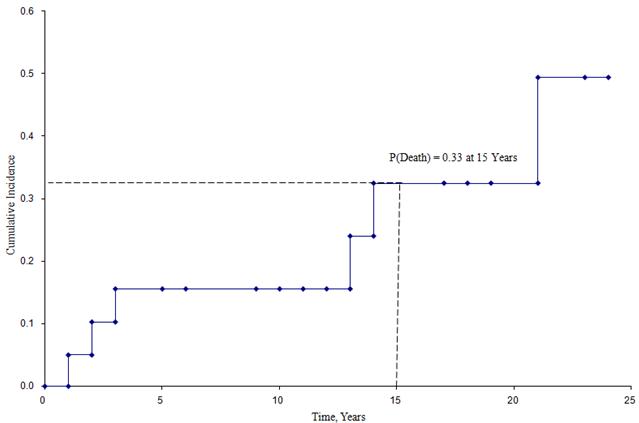
Na podstawie tego wykresu możemy oszacować prawdopodobieństwo, że uczestnik umrze do określonego punktu czasowego. Na przykład, prawdopodobieństwo śmierci wynosi około 33% w wieku 15 lat (patrz linie przerywane).

powrót do góry | poprzednia strona | następna strona

.