Przepływ StatsTest: Predykcja >>Ciągła zmienna zależna >>Więcej niż jedna zmienna niezależna >>Brak powtórzeń >>Jedna zmienna zależna
Nie jesteś pewien, czy to właściwa metoda statystyczna? Użyj przepływu pracy Choose Your StatsTest, aby wybrać właściwą metodę.
- What is Multivariate Multiple Linear Regression?
- Assumptions for Multivariate Multiple Linear Regression
- Liniowość
- Brak wartości odstających
- Podobny rozrzut w całym zakresie
- Normalność reszt
- No Multicollinearity
- Kiedy używać wielorakiej liniowej regresji wielorakiej?
- Predykcja
- Ciągła zmienna zależna
- Więcej niż jedna zmienna niezależna
- Wieloraka regresja liniowa Przykład
- Często zadawane pytania
- Help!
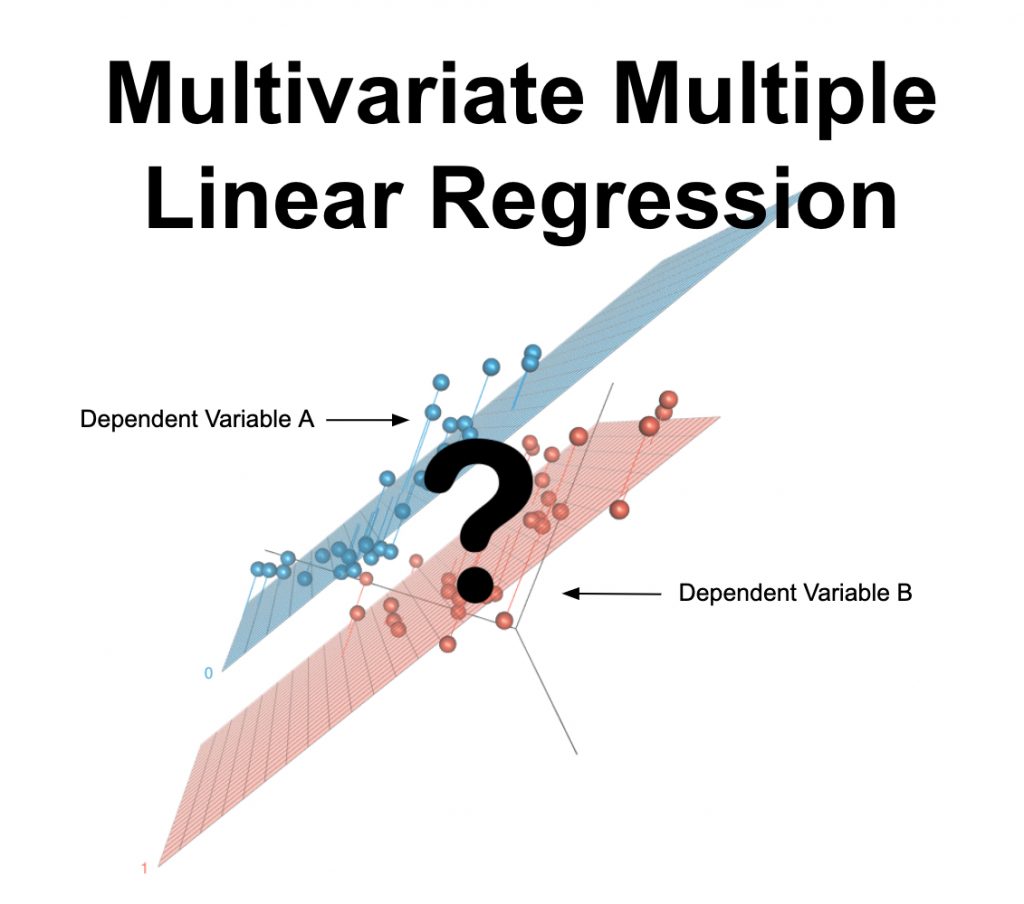
What is Multivariate Multiple Linear Regression?
Multivariate Multiple Linear Regression jest testem statystycznym używanym do przewidywania wielu zmiennych wyniku przy użyciu jednej lub więcej innych zmiennych. Jest on również używany do określenia liczbowego związku między tymi zestawami zmiennych i innymi. Zmienna, którą chcesz przewidzieć powinna być ciągła, a twoje dane powinny spełniać inne założenia wymienione poniżej.
Assumptions for Multivariate Multiple Linear Regression
Każda metoda statystyczna ma założenia. Założenia oznaczają, że twoje dane muszą spełniać pewne właściwości, aby wyniki metody statystycznej były dokładne.
Założenia dla wieloczynnikowej regresji liniowej obejmują:
- Liniowość
- Brak wartości odstających
- Podobny rozrzut w całym zakresie
- Normalność reszt
- Brak wieloliniowości
Zanurzmy się w każdym z nich osobno.
Liniowość
Zmienne, na których Ci zależy muszą być powiązane liniowo. Oznacza to, że jeśli wykreślisz zmienne, będziesz w stanie narysować linię prostą, która pasuje do kształtu danych.
Brak wartości odstających
Zmienne, którymi się zajmujesz, nie mogą zawierać wartości odstających. Regresja liniowa jest wrażliwa na wartości odstające lub punkty danych, które mają wyjątkowo duże lub małe wartości. Możesz powiedzieć, czy twoje zmienne mają wartości odstające, wykreślając je i obserwując, czy jakieś punkty są daleko od wszystkich innych punktów.
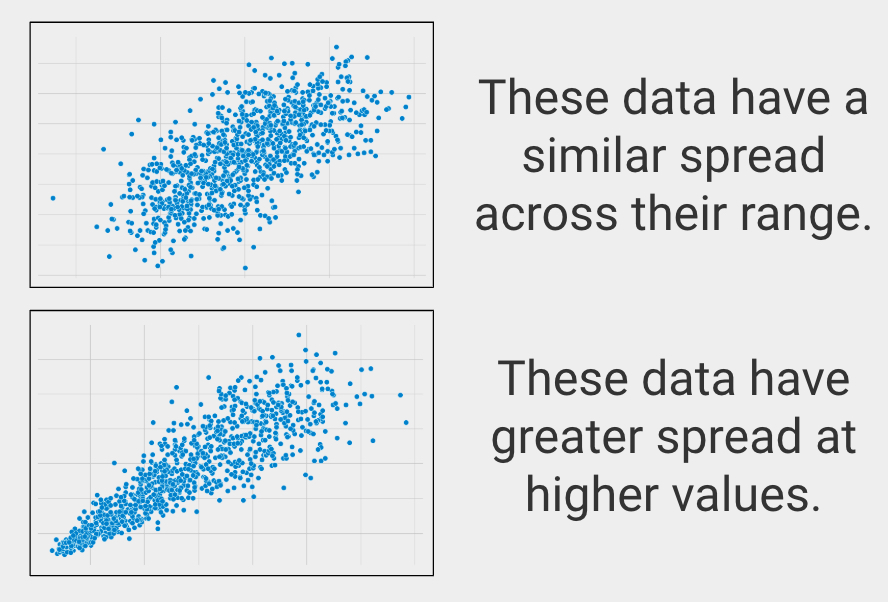
Podobny rozrzut w całym zakresie
W statystyce nazywa się to homoscedastycznością, która opisuje, kiedy zmienne mają podobny rozrzut w całym zakresie.
Normalność reszt
Słowo “reszty” odnosi się do wartości wynikających z odjęcia oczekiwanych (lub przewidywanych) zmiennych zależnych od wartości rzeczywistych. The distribution of these values should match a normal (or bell curve) distribution shape.
Spełnienie tego założenia zapewnia, że wyniki regresji są jednakowo stosowalne w całym zakresie danych i że nie ma systematycznej tendencyjności w przewidywaniu.
No Multicollinearity
Multicollinearity odnosi się do scenariusza, w którym dwie lub więcej niezależnych zmiennych są znacząco skorelowane między sobą. Kiedy wieloliniowość jest obecna, współczynniki regresji i istotność statystyczna stają się niestabilne i mniej wiarygodne, chociaż nie ma to wpływu na to, jak dobrze model pasuje do danych per se.
Kiedy używać wielorakiej liniowej regresji wielorakiej?
Powinieneś użyć Wielowymiarowej Wielokrotnej Regresji Liniowej w następującym scenariuszu:
- Chcesz użyć jednej zmiennej w przewidywaniu wielu innych zmiennych lub chcesz określić liczbowo związek między nimi
- Zmienne, które chcesz przewidywać (twoja zmienna zależna), są ciągłe
- Masz więcej niż jedną zmienną niezależną, lub jedną zmienną, której używasz jako predyktora
- Nie masz powtarzających się pomiarów z tej samej jednostki obserwacji
- Masz więcej niż jedną zmienną zależną
Wyjaśnijmy to, aby pomóc ci wiedzieć, kiedy używać regresji liniowej wielorakiej.
Predykcja
Szukasz testu statystycznego do przewidywania jednej zmiennej za pomocą innej. To jest pytanie o przewidywanie. Inne rodzaje analiz obejmują badanie siły związku między dwiema zmiennymi (korelacja) lub badanie różnic między grupami (różnica).
Ciągła zmienna zależna
Zmienna, którą chcesz przewidzieć, musi być ciągła. Ciągła oznacza, że twoja zmienna zainteresowania może w zasadzie przyjąć dowolną wartość, taką jak tętno, wzrost, waga, liczba batoników lodowych, które możesz zjeść w ciągu 1 minuty, itp.
Typy danych, które NIE są ciągłe obejmują dane uporządkowane (takie jak miejsce w wyścigu, najlepsze rankingi biznesowe, itp.), dane kategoryczne (płeć, kolor oczu, rasa, itp.) lub dane binarne (kupił produkt lub nie, ma chorobę lub nie, itp.).
Jeśli twoja zmienna zależna jest binarna, powinieneś użyć Wielokrotnej regresji logistycznej, a jeśli twoja zmienna zależna jest kategoryczna, to powinieneś użyć Wielomianowej regresji logistycznej lub Liniowej analizy dyskryminacyjnej.
Więcej niż jedna zmienna niezależna
Liniowa regresja wieloraka jest używana, kiedy jest jedna lub więcej zmiennych przewidujących z wieloma wartościami dla każdej jednostki obserwacji.
Bez powtórzonych środków
Ta metoda jest odpowiednia dla scenariusza, kiedy jest tylko jedna obserwacja dla każdej jednostki obserwacji. The unit of observation is what composes a “data point”, for example, a store, a customer, a city, etc…
If you have one or more independent variables but they are measured for the same group at multiple points in time, then you should use a Mixed Effects Model.
Więcej niż jedna zmienna zależna
Aby uruchomić wielozmiennową regresję liniową, powinieneś mieć więcej niż jedną zmienną zależną lub zmienną, którą próbujesz przewidzieć.
Jeśli przewidujesz tylko jedną zmienną, powinieneś użyć wielorakiej regresji liniowej.
Wieloraka regresja liniowa Przykład
Zmienna zależna 1: Przychody
Zmienna zależna 2: Ruch klientów
Zmienna niezależna 1: Dolary wydane na reklamę przez miasto
Independent Variable 2: Populacja miasta
Hipoteza zerowa, która jest statystyczny lingo dla tego, co by się stało, gdyby leczenie nic nie robi, jest to, że nie ma związku między wydać na reklamę i dolarów reklamowych lub ludności przez miasto. Nasz test będzie ocenić prawdopodobieństwo tej hipotezy jest true.
Zbieramy nasze dane i po upewnieniu się, że założenia regresji liniowej są spełnione, wykonujemy analysis.
Ta analiza skutecznie uruchamia wielokrotną regresję liniową dwa razy przy użyciu obu zmiennych zależnych. Tak więc, kiedy uruchamiamy tę analizę, otrzymujemy współczynniki beta i wartości p dla każdego terminu w modelu “przychody” i w modelu “ruch klientów”. Dla każdego modelu regresji liniowej, będziesz miał jeden współczynnik beta, który jest równy punktowi przecięcia linii regresji liniowej (często oznaczany jako 0 jako β0). Jest to po prostu miejsce, w którym linia regresji przecina oś y, gdybyś miał wykreślić swoje dane. W przypadku wielokrotnej regresji liniowej istnieją dodatkowo jeszcze dwa inne współczynniki beta (β1, β2 itd.), które reprezentują związek między zmiennymi niezależnymi i zależnymi.
Te dodatkowe współczynniki beta są kluczem do zrozumienia liczbowego związku między twoimi zmiennymi. Zasadniczo, dla każdej jednostki (wartość 1) wzrost w danej zmiennej niezależnej, twoja zmienna zależna ma się zmienić o wartość współczynnika beta związanego z tej zmiennej niezależnej (przy utrzymaniu innych zmiennych niezależnych stałych).
Wartość p związana z tymi dodatkowymi wartościami beta jest szansa zobaczenia naszych wyników przy założeniu, że faktycznie nie ma związku między tą zmienną a przychodem. Wartość p mniejsza lub równa 0,05 oznacza, że nasz wynik jest statystycznie istotny i możemy ufać, że różnica nie wynika tylko z przypadku. Aby uzyskać ogólną wartość p dla modelu i indywidualne wartości p, które reprezentują efekty zmiennych w dwóch modelach, MANOVAs są często używane.
Dodatkowo, analiza ta będzie skutkować wartością R-Squared (R2). Wartość ta może mieścić się w zakresie 0-1 i reprezentuje, jak dobrze linia regresji liniowej pasuje do punktów danych. Im wyższa wartość R2, tym lepiej twój model pasuje do twoich danych.
Często zadawane pytania
Q: Jaka jest różnica między wieloczynnikową wielokrotną regresją liniową a wielokrotnym uruchamianiem regresji liniowej?
A: Są one koncepcyjnie podobne, ponieważ poszczególne współczynniki modelu będą takie same w obu scenariuszach. Istotną różnicą jest jednak to, że testy istotności i przedziały ufności dla wielorakiej regresji liniowej uwzględniają wiele zmiennych zależnych.
Q: Jak uruchomić wieloraką regresję liniową w SPSS, R, SAS lub STATA?
A: Ten zasób jest skoncentrowany na pomocy w wyborze właściwej metody statystycznej za każdym razem. Istnieje wiele dostępnych zasobów, które pomogą Ci dowiedzieć się, jak uruchomić tę metodę na Twoich danych:
Artykuł R: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/
Help!
Jeśli nadal nie możesz czegoś rozgryźć, nie krępuj się
.