6.3 Sieci przekonań
Pojęcie warunkowej niezależności może być użyte do zwięzłego przedstawienia wielu dziedzin. Idea polega na tym, że biorąc pod uwagę zmienną losową X, może istnieć mały zbiór zmiennych, które bezpośrednio wpływają na wartość zmiennej w tym sensie, że X jest bezwarunkowo niezależny od innych zmiennych, biorąc pod uwagę wartości zmiennych bezpośrednio wpływających. Zbiór lokalnie wpływających zmiennych nazywany jest kocem Markowa. Ta lokalność jest wykorzystywana w sieciach przekonań. Sieć przekonań jest skierowanym modelem warunkowej zależności pomiędzy zestawem zmiennych losowych. Precyzyjne stwierdzenie warunkowej niezależności w sieci przekonań uwzględnia kierunkowość.
Aby zdefiniować sieć przekonań, należy zacząć od zbioru zmiennych losowych, które reprezentują wszystkie cechy modelu. Załóżmy, że zmienne te to {X1,…,Xn}.Następnie wybierz całkowite uporządkowanie zmiennych, X1,…,Xn.
Reguła łańcucha (Proposition 6.3) pokazuje, jak zdekomponować koniunkcję na prawdopodobieństwa bezwarunkowe:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Or, in terms of random variables and probability distributions,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definiujemy rodziców zmiennej losowej Xi, zapisanych jako rodzice(Xi), jako aminimalny zbiór poprzedników Xi w całkowitym uporządkowaniu, takich, że pozostałe poprzedniki Xi są warunkowo niezależne od Xi, biorąc pod uwagę rodziców(Xi). Oznacza to, że parents(Xi) ⊆{X1,…,Xi-1} takie, że
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Jeśli istnieje więcej niż jeden zbiór minimalny, to każdy zbiór minimalny może być wybrany na rodziców. Może istnieć więcej niż jeden zbiór minimalny tylko wtedy, gdy niektóre z poprzedników są deterministycznymi funkcjami innych zbiorów.
Możemy połączyć regułę łańcuchową i definicję rodziców, co daje
P(X1, X2,—, Xn) = ∏i=1n P(Xi|rodzice(Xi)).
Prawdopodobieństwo na wszystkich zmiennych, P(X1, X2,—,Xn), nazywamy wspólnym rozkładem prawdopodobieństwa. Sieć przekonań definiuje faktoryzację wspólnego rozkładu prawdopodobieństwa, gdzie prawdopodobieństwa warunkowe tworzą czynniki, które są mnożone razem.
Sieć przekonań, zwana również siecią bayesowską, jest acyklicznym grafem skierowanym (DAG), gdzie węzły są zmiennymi losowymi. Od każdego elementuparents(Xi) do Xi istnieje łuk.Związany z siecią przekonań jest zestaw warunkowych rozkładów prawdopodobieństwa – warunkowe prawdopodobieństwo każdej zmiennej biorąc pod uwagę jej rodziców (co zawiera wcześniejsze prawdopodobieństwa tych zmiennych, które nie mają rodziców).
Tak więc, sieć przekonań składa się z
- DAG, gdzie każdy węzeł jest oznaczony zmienną losową;
- dziedziny dla każdej zmiennej losowej; i
- zestawu rozkładów prawdopodobieństwa warunkowego dających P(X|parents(X)) dla każdej zmiennej X.
Sieć przekonań jest acykliczna z konstrukcji. Sposób w jaki łańcuch rządzący rozkłada koniunkcję daje uporządkowanie. Zmienna może mieć tylko poprzedników jako rodziców.
Załóżmy, że użyjemy następujących zmiennych, z których wszystkie są logiczne, w następującej kolejności:
- Sabotaż jest prawdą, gdy nastąpiła manipulacja przy alarmie.
- Pożar jest prawdziwy, gdy jest pożar.
- Alarm jest prawdziwy, gdy rozlega się alarm.
- Dym jest prawdziwy, gdy jest dym.
- Opuszczenie jest prawdziwe, gdy wiele osób opuszcza budynek naraz.
- Zgłoszenie jest prawdziwe, gdy ktoś zgłasza opuszczenie budynku. Raport jest fałszywy, jeśli nie ma raportu o wychodzeniu.
Zmienna Raport oznacza raport czujnika, że ludzie wychodzą. Informacja ta jest niewiarygodna, ponieważ osoba wydająca taki meldunek może grać praktyczny żart, lub nikt, kto mógłby wydać taki meldunek, mógł nie zwracać uwagi. Zmienna ta została wprowadzona, aby umożliwić warunkowanie na niewiarygodnych danych z czujników. Agent wie, co zgłasza czujnik, ale ma tylko niewiarygodny dowód na to, że ludzie opuszczają budynek.W ramach dziedziny zakładamy następujące niezależności warunkowe:
- Pożar jest warunkowo niezależny od sabotażu (przy braku innych informacji).
- Alarm zależy zarówno od pożaru, jak i od sabotażu. To znaczy, nie przyjmujemy żadnych założeń o niezależności tego, jak Alarm zależy od swoich poprzedników, biorąc pod uwagę tę kolejność zmiennych.
- Dym zależy tylko od Ognia i jest warunkowo niezależny od Sabotażu i Alarmu, biorąc pod uwagę, czy jest Pożar.
- Odejście zależy tylko od Alarmu, a nie bezpośrednio od Ognia lub Sabotażu lub Dymu. Oznacza to, że Opuszczenie jest warunkowo niezależne od pozostałych zmiennych, biorąc pod uwagę Alarm.
- Raport zależy tylko bezpośrednio od Opuszczenia.
Sieć przekonań z rysunku 6.1 wyraża te zależności.
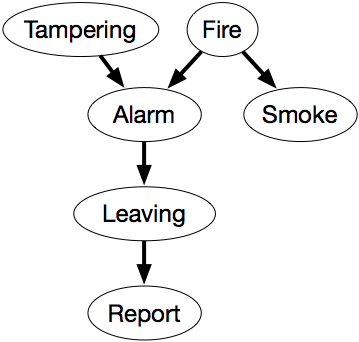
Sieć ta reprezentuje faktoryzację
P(Sabotaż,Pożar,Alarm,Dym,Opuszczenie,Raport) = P(Tampering) ×P(Fire) ×P(Alarm|Tampering,Fire) ×P(Smoke|Fire) ×P(Leaving|Alarm) ×P(Report|Leaving).
Musimy również określić dziedzinę każdej zmiennej. Przyjmijmy, że zmienne są boolowskie, czyli mają dziedzinę {true,false}. Używamy wariantu zmiennej pisanej małymi literami do reprezentowania wartości prawdziwej i używamy negacji dla wartości fałszywej. Tak więc, na przykład, Tampering=true jest zapisywane jako tampering, a Tampering=false jest zapisywane jako ¬tampering.
Następujące przykłady zakładają następujące prawdopodobieństwa warunkowe:
P(pożar) = 0.01
P(alarm | pożar ∧tampering) = 0.5
P(alarm | pożar ∧¬tampering) = 0,99
P(alarm | ¬pożar ∧tampering) = 0,85
P(alarm | ¬pożar ∧¬tampering) = 0,0001
P(dym | pożar ) = 0.9
P(dym | ¬pożar ) = 0,01
P(wyjście | alarm ) = 0,88
P(wyjście | ¬alarm ) = 0,001
P(raport | wyjście ) = 0,75
P(raport | ¬wyjazd ) = 0.01
- Dla każdego przewodu wi istnieje zmienna losowa, Wi, z dziedziny {live,dead}, która oznacza, czy w przewodzie wi jest zasilanie. Wi=live oznacza, że przewód wi ma zasilanie. Wi=dead oznacza, że w przewodzie wi nie ma prądu.
- Zmienna Outside_power z dziedziną {live,dead} oznacza, czy do budynku dochodzi prąd.
- Dla każdego wyłącznika si, zmienna Si_pos oznacza położenie si. Ma ona dziedzinę {up,down}.
- Dla każdego przełącznika si, zmienna Si_st oznacza stan przełącznika si. Ma ona dziedzinę {ok,upside_down,short,intermittent,broken}. Si_st=ok oznacza, że przełącznik si działa normalnie. Si_st=upside_down oznacza, że wyłącznik si jest zainstalowany do góry nogami. Si_st=short oznacza, że przełącznik si jest skrócony i działa jak przewód. Si_st=broken oznacza, że przełącznik si jest uszkodzony i nie pozwala na przepływ prądu.
- Dla każdego wyłącznika, zmienna Cbi_st ma dziedzinę {on,off}. Cbi_st=on oznacza, że prąd może przepływać przez cbi, a Cbi_st=off oznacza, że prąd nie może przepływać przez cbi.
- Dla każdego światła li, zmienna Li_st z dziedziną {ok,intermittent,broken} oznacza stan światła. Li_st=ok oznacza, że lampka li będzie świecić, jeśli jest zasilana, Li_st=intermittent oznacza, że lampka li świeci z przerwami, jeśli jest zasilana, a Li_st=brok oznacza, że lampka li nie działa.
Wybierzmy uporządkowanie, w którym przyczyny zmiennej są przed zmienną w uporządkowaniu. Na przykład zmienna określająca, czy światło jest zapalone, pojawia się po zmiennych określających, czy światło działa i czy do światła dochodzi prąd.
To, czy światło l1 jest zapalone, zależy tylko od tego, czy w przewodzie w0 jest prąd i czy światło l1 działa prawidłowo. Othervariables, such as the position of switch s1, whether light l2is lit, or who is the Queen of Canada, are irrelevant. Tak więc rodzicami L1_lit są W0 i L1_st.
Rozważmy zmienną W0, która reprezentuje, czy w przewodzie w0 jest prąd. Gdybyśmy wiedzieli, czy w przewodach w1 i w2 jest prąd, i znali położenie przełącznika s2 oraz to, czy przełącznik działa prawidłowo, wartość pozostałych zmiennych (poza L1_lit) nie miałaby wpływu na nasze przekonanie o tym, czy w przewodzie w0 jest prąd. Zatem rodzicami W0 powinny być S2_Pos, S2_st,W1 i W2.
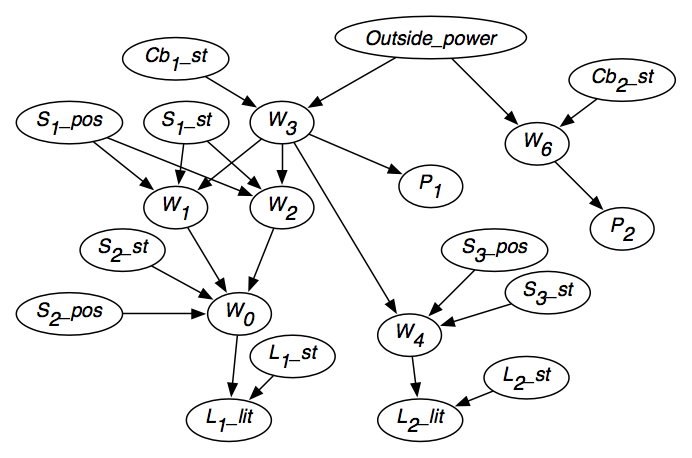
Rysunek 6.2 przedstawia wynikową sieć przekonań po uwzględnieniu niezależności każdej zmiennej.Sieć przekonań zawiera również domeny zmiennych, podane na rysunku, oraz prawdopodobieństwa warunkowe każdej zmiennej z uwzględnieniem jej rodziców.
Dla zmiennej W1 należy określić następujące prawdopodobieństwa warunkowe:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok. ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=live|S1_pos=down ∧S1_st=brok ∧W3=dead).
Istnieją dwie wartości dla S1_pos, pięć wartości dla S1_ok i dwie wartości dla W3, więc istnieje 2×5×2 = 20 różnych przypadków, w których należy określić wartość dla W1=live. Jeśli chodzi o teorię prawdopodobieństwa, to prawdopodobieństwo dla W1=live dla tych 20 przypadków może być przypisane arbitralnie. Oczywiście, znajomość dziedziny ogranicza to, jakie wartości mają sens. Wartości dla W1=martwy można obliczyć z wartości dla W1=żywy dla każdego z tych przypadków.
Ponieważ zmienna S1_st nie ma rodziców, wymaga ona wcześniejszego rozkładu, który można określić jako prawdopodobieństwa dla wszystkich wartości oprócz jednej; pozostałą wartość można wyprowadzić z ograniczenia, że wszystkie prawdopodobieństwa sumują się do 1. Zatem, aby określić rozkład S1_st, należy określić cztery z pięciu następujących prawdopodobieństw:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Sieć przekonań jest graficzną reprezentacją warunkowej niezależności. Niezależność pozwala nam na przedstawienie bezpośrednich efektów w obrębie grafu i nakazuje, które prawdopodobieństwa muszą być określone. Arbitralne prawdopodobieństwa wtórne mogą być wyprowadzone z sieci.
Założenie niezależności osadzone w sieci przekonań jest następujące:Każda zmienna losowa jest warunkowo niezależna od swoich nie-potomków, biorąc pod uwagę jej rodziców. To znaczy, jeśli X jest zmienną losową z rodzicami Y1,…, Yn, wszystkie zmienne losowe, które nie są potomkamiX są warunkowo niezależne od X biorąc pod uwagę Y1 ,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
jeśli R nie dotyczy potomka X. Dla tej definicji, włączamy X jako potomka samego siebie. Prawa strona tego równania jest formą prawdopodobieństw, które są określone jako część sieci przekonań. R może dotyczyć przodków X i innych węzłów tak długo, jak długo nie są one potomkami X. Założenie niezależności mówi, że cały wpływ zmiennych nie będących potomkami jest uchwycony przez znajomość wartości rodziców X.
Często odnosimy się tylko do etykietowanego DAG jako sieci przekonań. W takim przypadku należy pamiętać, że domena każdej zmiennej i zbiór rozkładów prawdopodobieństwa warunkowego są również częścią sieci.
Liczba prawdopodobieństw, które muszą być określone dla każdej zmiennej jest wykładnicza w liczbie rodziców tej zmiennej.Założenie niezależności jest użyteczne o tyle, o ile liczba zmiennych, które bezpośrednio wpływają na inną zmienną jest mała. Powinieneś uporządkować zmienne tak, aby węzły miały jak najmniej rodziców, jak to tylko możliwe.
Sieci przekonań i przyczynowość
Sieci przekonań często nazywane są sieciami przyczynowymi i twierdzono, że stanowią dobrą reprezentację przyczynowości.Przypomnijmy, że model przyczynowy przewiduje wynik interwencji.Załóżmy, że masz w umyśle model przyczynowy domeny, gdzie domena jest określona w kategoriach zbioru zmiennych losowych. Dla każdej pary zmiennych losowych X1i X2, jeśli istnieje bezpośredni związek przyczynowy od X1 do X2 (tzn. interwencja zmieniająca X1 w pewnym kontekście innych zmiennych wpływa na X2 i nie może to być modelowane przez posiadanie jakiejś zmiennej interweniującej), dodajemy łuk odX1 do X2. Można by się spodziewać, że model przyczynowy będzie zgodny z założeniem o niezależności sieci przekonań. W ten sposób wszystkie wnioski sieci przekonań byłyby ważne.
Oczekiwałbyś również, że taki graf będzie acykliczny; nie chcesz, aby coś ostatecznie powodowało samo siebie. To założenie jest rozsądne, jeśli weźmiemy pod uwagę, że zmienne losowe reprezentują konkretne zdarzenia, a nie typy zdarzeń. Na przykład, rozważmy łańcuch przyczynowy, w którym “bycie zestresowanym” powoduje, że “pracujesz nieefektywnie”, co z kolei powoduje, że “jesteś zestresowany”. Aby przerwać ten pozorny cykl, możemy reprezentować “bycie zestresowanym” na różnych etapach jako różne zmienne losowe, które odnoszą się do różnych czasów. Bycie zestresowanym w przeszłości powoduje, że nie pracujemy dobrze w tej chwili, co powoduje, że jesteśmy zestresowani w przyszłości. Zmienne powinny spełniać zasadę jasności i mieć dobrze zdefiniowane znaczenie. Zmienne nie powinny być postrzegane jako typy zdarzeń.
Sieć przekonań sama w sobie nie ma nic do powiedzenia na temat przyczynowości i może reprezentować nie przyczynową niezależność, ale wydaje się szczególnie odpowiednia, gdy istnieje przyczynowość w dziedzinie. Dodanie łuków, które reprezentują lokalną przyczynowość, prowadzi do powstania małej sieci przekonań. Sieć przekonań z Rysunku 6.2 pokazuje, jak można to zrobić dla prostej dziedziny.
Sieć przyczynowo-skutkowa modeluje interwencje. Jeśli ktoś sztucznie zmusiłby zmienną do przyjęcia określonej wartości, miałoby to wpływ na potomków tej zmiennej, ale nie na inne węzły. Wreszcie, można zobaczyć jak przyczynowość w sieciach przekonań odnosi się do rozumowania przyczynowego i dowodowego omówionego w rozdziale 5.7. Przyczynową sieć przekonań można postrzegać jako dalszą część aksjomatyzacji w kierunku przyczynowym. Rozumowanie w sieciach przekonań odpowiada wnioskowaniu o przyczynach, a następnie przewidywaniu na ich podstawie. Istnieje bezpośrednie odwzorowanie pomiędzy logicznym poglądem opartym na indukcji, omówionym w rozdziale 5.7, a sieciami przekonań: Sieci przekonań mogą być modelowane jako programy logiczne z prawdopodobieństwami nad możliwymi hipotezami. Jest to opisane w rozdziale 14.3.
Zwróć uwagę na ograniczenie “każda zmienna losowa jest warunkowo niezależna od swoich nie-potomków, biorąc pod uwagę jej rodziców” w definicji niezależności zakodowanej w sieci przekonań. JeśliR zawiera potomka zmiennej X, to założenie o niezależności nie ma bezpośredniego zastosowania.
Zmienna S1_pos nie ma rodziców. Zatem, niezależność wbudowana w sieć przekonań określa, że P(S1_pos=up|A) =P(S1_pos=up) dla dowolnego A, które nie zawiera potomka S1_pos. Jeśli A zawiera potomka S1_pos=up – na przykład, jeśli A jest S2_pos=up∧L1_lit=true – założenie niezależności nie może być bezpośrednio zastosowane.
Sieć ta może być użyta na wiele sposobów:
- Uwarunkowując się od wiedzy, że wyłączniki i obwody są w porządku, oraz od wartości mocy zewnętrznej i położenia wyłączników, sieć ta może symulować jak powinno działać oświetlenie.
- Dając wartości mocy zewnętrznej i pozycji przełączników, sieć może wywnioskować prawdopodobieństwo każdego wyniku – na przykład, jak prawdopodobne jest, że l1 jest zapalone.
- Podając wartości przełączników i to, czy światła są zapalone, można wywnioskować prawdopodobieństwo następcze, że każdy przełącznik lub wyłącznik jest w dowolnym stanie.
- Dając pewne obserwacje, sieć może być użyta do rozumowania wstecz, aby określić najbardziej prawdopodobne położenie przełączników.
- Dając pewne pozycje przełączników, pewne wyjścia i pewne wartości pośrednie, sieć może być użyta do określenia prawdopodobieństwa każdej innej zmiennej w sieci.
Sieć przekonań określa wspólny rozkład prawdopodobieństwa, z którego można wyprowadzić dowolne prawdopodobieństwa warunkowe. Sieć może być zapytana przez zapytanie o warunkowe prawdopodobieństwo dowolnej zmiennej uwarunkowane wartościami innych zmiennych. Przykład 6.13: Rozważmy przykład 6.10. Wcześniejsze prawdopodobieństwa (przy braku dowodów) każdej zmiennej mogą być obliczone przy użyciu metod z następnej sekcji. Następujące prawdopodobieństwa warunkowe wynikają z modelu z przykładu 6.10, do około trzech miejsc po przecinku:
P(pożar) = 0.01
P(zgłoszenie ) = 0.028
P(dym) = 0.0189
Obserwacja raportu daje następujące wyniki:
P(pożar |raport)= 0.2305
P(dym |raport) = 0.215
Jak można się spodziewać, prawdopodobieństwo zarówno manipulacji jak i pożaru wzrasta przez raport. Ponieważ prawdopodobieństwo pożaru jest zwiększone, prawdopodobieństwo dymu jest również zwiększone.
Załóżmy, że zamiast tego zaobserwowano dym:
P(pożar|dym) = 0.476
P(raport |dym) = 0.320
Zauważmy, że obserwacja dymu nie ma wpływu na prawdopodobieństwo manipulacji; jednak prawdopodobieństwa raportu i pożaru wzrastają.
Załóżmy, że zaobserwowano zarówno zgłoszenie jak i dym:
P(pożar |zgłoszenie ∧ dym) = 0.964
Zaobserwowanie obu czyni pożar jeszcze bardziej prawdopodobnym. Jednakże, w kontekście raportu, obecność dymu sprawia, że manipulowanie jest mniej prawdopodobne. Dzieje się tak, ponieważ raport jest wyjaśniony przez ogień, który jest teraz bardziej prawdopodobny.
Załóżmy, że zaobserwowano raport, ale nie dym:
P(pożar|raport ∧¬dym) = 0,0294
W kontekście raportu, pożar staje się znacznie mniej prawdopodobny, a zatem prawdopodobieństwo manipulacji wzrasta, aby wyjaśnić raport.
Przykład ten ilustruje, jak założenie o niezależności sieci przekonań daje konkluzje, a także pokazuje, jak wyjaśnianie jest konsekwencją założenia o niezależności sieci przekonań.
- 6.3.1 Konstruowanie sieci przekonań
.