Tetraedr

Zawartość tej strony Co to jest Tetraedr? Części czworościanu Liczby czworościanów Czworościan w sześcianie Pierścienie czworościanów Czworościany w Internecie

Do strony głównej “Mathematische Basteleien”

Co to jest czworościan?

Czworościan to trójwymiarowa figura z czterema równobocznymi trójkątami. Jeśli podniesiemy trzy trójkąty (1), otrzymamy czworościan w widoku z góry (2). Zazwyczaj jest on pokazywany w perspektywie (3).

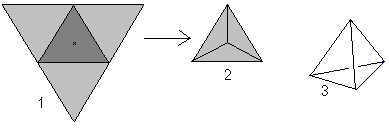
Jeśli spojrzysz na słowo tetrahedron (tetrahedron znaczy “z czterema płaszczyznami”), możesz nazwać każdą piramidę z trójkątem jako podstawą tetrahedronem.

Jednakże czworościan jest prostym, regularnym trójkątnym ostrosłupem na tej stronie.

Części czworościanu
Wysokość i pole trójkąta bocznego
Cztery trójkąty równoboczne tworzą czworościan.

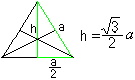…	Wybieramy trójkąt: Trzy wysokości przecinają się wzajemnie w jednym punkcie, jak w każdym trójkącie. Jest to środek trójkąta. Wysokość można obliczyć na podstawie boku a jako h=sqr(3)/2*a korzystając z twierdzenia pitagorejskiego.

Wysokości są także środkowymi i przecinają się w stosunku 2:1. Wykorzystujemy to w poniższych obliczeniach.

Pole powierzchni trójkąta to A=sqr(3)/4*a².

Wysokość przestrzenna

Wysokość czworościanu foremnego znajduje się między środkiem trójkąta podstawowego (1) a wierzchołkiem (2). Do obliczeń bierzemy pod uwagę tak zwany trójkąt pomocniczy (3, żółty), który jest utworzony przez jedną krawędź i dwie wysokości trójkąta. Jest H=sqr(6)/3*a z wykorzystaniem twierdzenia Pitagorasa.
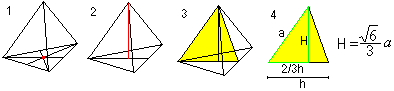
Środek, sfera wpisana i sfera wpisanaŚrodek czworościanu foremnego jest punktem przecięcia dwóch wysokości przestrzennych (1,2,3). Jest to środek ciężkości, środek kuli przechodzącej przez cztery rogi oraz środek największej kuli, która nadal mieści się w czworościanie (4).

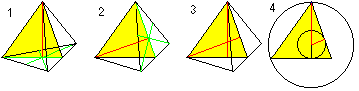
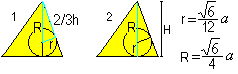…	Otrzymujemy dwa wzory na r i R z pomocą twierdzenia pythagorejskiego (1) i H=R+r (2): Jest r=sqr(6)/12*a , R=sqr(6)/4*a.

Powierzchnia kątowa

….…..

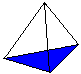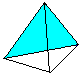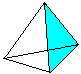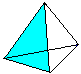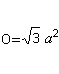Powierzchnia podstawy i powierzchnie boczne tworzą powierzchnięO. Jest O=4*A (trójkąt) = sqr(3)a².

Objętość

Tetrahedal Numbers top

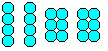……	Jeśli skleisz 20 kulek w dwie grupy z czwórkami i dwie z szóstkami, otrzymasz dobrze znaną łamigłówkę: Musisz ułożyć piramidę z czterech kawałków.

Podobnych łamigłówek jest wiele.

Tetrahedron w sześcianie góra
Sześć przekątnych twarzy tworzy czworościan w sześcianie.
Jeśli wiesz, 3D-view, można trójwymiarowo spojrzeć na następujące dwie pary sześcianów.

Objętość czworościanu jest trzecią częścią objętości sześcianu.

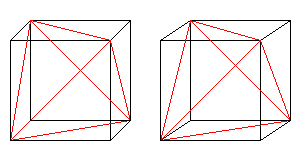
Jeśli narysujesz drugi czworościan i linie przecięcia, otrzymasz przenikanie dwóch czworościanów.

Figura składa się z przekątnych ścian i linii łączących środki bocznych kwadratów oryginalnego sześcianu. Ostatnie tony tworzą ośmiościan.

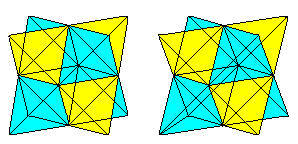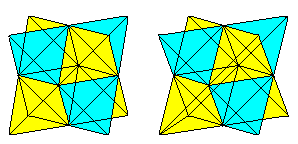
Pierścienie czworościanów górą
Możesz zrobić papierowe czworościany i przykleić ich parzystą liczbę do pierścienia. Pierścień może się ciągle skręcać do wewnątrz lub na zewnątrz przez środek. Jest to bardzo ładna zabawka. – Takie pierścienie są również nazywane kalejdocyklami.Więcej znajdziesz na mojej stronie internetowej Kaleidocycles.

Tetrahedraon the Internettop

Niemiecki

Christof Weber
Washat dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
Tetraeder Sierpińskiego

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

język angielski

Eric W. Weisstein (World of Mathematics)
Tetrahedron

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetrahedron

Joyce Frost i Peg Cagle (mathforum)
AnAmazing, Space Filling, Non-regular Tetrahedron

Wikipedia
Tetrahedron,Tetrapod(structure), Tetrahedralnumber

.