By Evan Ma

(Math and Physics tutor at The Edge Learning Center)

Funkcja logarytmiczna wydaje się dezorientować wielu uczniów studiujących program IB Math SL. Aby ją właściwie zrozumieć, zdefiniujmy

gdzie , ściśle dodatnia liczba rzeczywista, jest nazywana podstawą, a jest potęgą. Na przykład, wszyscy znamy na pamięć następujące wyrażenia:

i tak dalej. Funkcja logarytmiczna robi to odwrotnie – podając jako argument liczbę, oblicza jej potęgę o określonej podstawie, a więc definiuje się ją następująco.

Jeśli

to

Więc jasne jest, że

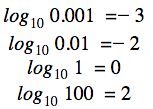
i tak dalej. Przyjrzyjmy się innym przykładom z udziałem innych zasad:

W ramach ćwiczeń uzupełnijmy poniższe pytania: (a) , (b) , (c) , (d) . Odpowiedzi znajdują się na końcu tego bloga.

Z definicji logarytmu wynika również, że jeśli podniesiemy podstawę o podstawę-logarytmu liczby rzeczywistej , to otrzymamy z powrotem liczbę , viz

Możesz spróbować to zweryfikować używając kalkulatora dla różnych ważnych podstaw. Tożsamość ta jest ważna, gdy próbujemy rozwiązywać równania logarytmiczne, których przykłady będziemy podawać dalej.

Przyjrzyjrzyjmy się teraz zasadom działania logarytmu. Podobnie jak w przypadku definicji logarytmu, wykorzystujemy prawa indeksów do wyprowadzenia następujących reguł:

1. Logarytm iloczynu jest sumą logarytmów

Dowód: Powiedzmy i , zatem

2. Podstawa logarytmu z Mr to razy

Proof: Powiedz , zatem

3. Logarytm ilorazu jest różnicą logarytmów

Dowód: Powiedzmy i , zatem

4. Ostatnia reguła nazywa się wzorem na zmianę podstawy. Posłużymy się przykładem jako narzędziem do wyprowadzenia tej formuły. Załóżmy, że chcemy wiedzieć, jaką potęgę liczby 2 należy podnieść, aby otrzymać 50. Ponieważ 50 nie jest całkowitą potęgą liczby 2, odpowiedź nie jest zbyt oczywista. Stąd piszemy

i stąd. Aby znaleźć , powiedzmy, że zastosujemy logarytm podstawy 10 do obu stron równania, ponieważ nasz kalkulator może nie mieć klawisza logarytmu podstawy 2:

Poprawione do 4 cyfr znaczących, wartość wynosi około 5,644. W rzeczywistości możesz sprawdzić swoją odpowiedź, podnosząc 2 do potęgi 5,644, aby zobaczyć, że odpowiedź wynosi około 50.

Aby uogólnić problem, powiedzmy, że musimy znaleźć takie, że i logarytm bazowy- nie jest do naszej dyspozycji, możemy więc zamiast tego użyć logarytmu bazowego zgodnie z równaniem

i dlatego

Przykładowo, rozważmy następującą sytuację. Załóżmy, że kwota 10 000 USD jest zdeponowana z oprocentowaniem 2,5% w skali roku, składanym co roku. Jak długo pieniądze muszą być przechowywane na koncie, aby urosły do 50 000 $?

Aby odpowiedzieć na pytanie, w zasadzie próbujemy znaleźć n takie, że

Ponieważ mój prosty kalkulator naukowy nie pozwala mi określić podstawy 1.025 dla klucza logarytmicznego, będę musiał polegać na formule zmiany podstawy i użyć podstawy 10, a zatem

Ponieważ odsetki są obliczane co roku, potrzeba 66 lat, aby wzrosły co najmniej 5-krotnie.

Poznając reguły logarytmów, wprowadzamy funkcję logarytmu naturalnego, czyli . Jest ona bazą-, gdzie jest wybitną liczbą irracjonalną ≈2,71828, której znaczenia w naukach ścisłych i matematyce nie sposób przecenić. Stąd logarytm podstawy definiuje się następująco.

If

then

Następnie przyjrzyjmy się dwóm przykładom, w których popełniane są częste błędy w rozwiązywaniu równań logarytmów. Sprawdź, czy potrafisz zidentyfikować ten błąd.

Gdzie jest błąd? Przyjrzyj się dokładniej. Oczywiście w drugim kroku nie można “dzielić” logarytmu przez znak dodawania. Pamiętaj, że możesz “podzielić” logarytm na sumę tylko wtedy, gdy logarytm jest zastosowany do iloczynu, a nie do sumy. Prawidłowe kroki są zatem następujące:

Przyjrzyjrzyjmy się następującemu przykładowi i sprawdźmy, czy potrafisz zidentyfikować błąd:

Gdzie jest błąd? Tak, w drugim kroku – iloraz logarytmów nie jest oczywiście logarytmem ilorazu. Możemy raczej skorzystać ze wzoru na zmianę podstawy, aby uprościć pierwszy krok, jak poniżej:

Na koniec zilustrujemy, jak wykorzystać reguły logarytmowania do rozwiązania następującego zadania:

Możesz zauważyć, że niewiadoma pojawia się jako podstawa i zmienna w argumencie logarytmu. W jaki sposób możemy rozwiązać ? Metoda nadal polega na konsekwentnym stosowaniu reguł logarytmu. Po pierwsze, podnosimy obie strony jako potęgi podstawy , a stąd

Przypominamy sobie z definicji logarytmu, że lewa strona stanie się po prostu argumentem logarytmu, a zatem

Przestawiając powyższe równanie, musimy rozwiązać

Zauważając, że przypomina to kwadraturę w , rozwiązujemy w następujący sposób:

Teraz, gdzie jest ujemny pierwiastek? Ponieważ jest również podstawą logarytmu, ujemny pierwiastek jest zatem odrzucany jako rozwiązanie. Stąd, jest ostateczną odpowiedzią.

Przeglądając powyższe przykłady, można się przekonać, że rozwiązanie pozornie trudnego równania logarytmicznego wcale nie jest trudne – wystarczy konsekwentnie stosować reguły logarytmowania i można otrzymać poprawne rozwiązanie.

Odpowiedzi na pytania: (a) 2 (b) 3 (c) -3 (d) -2.