Na początku zwykle konieczne jest zapoznanie się z wykresem pV cyklu. W tym celu prześledzimy krzywe procesu izochorycznego i adiabatycznego. Przybliżony wykres cyklu Otto jest przedstawiony na poniższym rysunku.
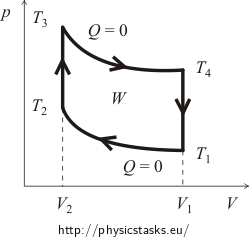
Sprawność η cyklu jest zdefiniowana jako
∗
gdzie W jest pracą wykonaną przez gaz w czasie jednego cyklu minus praca wykonana przez siły zewnętrzne (na wykresie jest ona reprezentowana przez powierzchnię obszaru wyznaczonego przez linie cyklu!), a Qsup jest ciepłem dostarczonym do układu podczas cyklu.
Pracę W można obliczyć korzystając z zależności pomiędzy ciśnieniem a objętością podczas adiabatycznego rozprężania i sprężania (praca wykonana podczas procesu izochorycznego jest oczywiście równa zeru). W tym zadaniu lepiej będzie jednak wykorzystać fakt, że całkowita zmiana energii wewnętrznej w cyklu musi być równa zeru (wracamy do tego samego stanu co na początku, a więc temperatura, a więc i energia wewnętrzna pozostają takie same!). Zgodnie z Pierwszym Prawem Termodynamiki pracę wykonaną przez gaz można wyrazić jako różnicę pomiędzy ciepłem Qsup dostarczonym a ciepłem Qrel oddanym. Wzór na sprawność cyklu ma więc postać
∗
Najpierw obliczymy ciepło dostarczone Qsup. Jest oczywiste, że podczas procesu adiabatycznego nie ma wymiany ciepła, a podczas chłodzenia izochorycznego ciepło jest uwalniane. Oznacza to, że ciepło będzie dostarczane tylko podczas izochorycznego ogrzewania od temperatury T2 do temperatury T3. Ilość tego ciepła można wyrazić za pomocą zmiennych: ilości substancji n w gazie oraz jego molowej pojemności cieplnej CV w następujący sposób:
W podobny sposób wyrazimy ilość wydzielonego ciepła Qrel. Wiemy już, że ciepło jest wydzielane tylko podczas izochorycznego ochładzania z temperatury T4 z powrotem do temperatury początkowej T1. To prawda, że:
Teraz podstawiamy te wzory do wzoru na sprawność cyklu i natychmiast otrzymujemy:
Teraz będziemy musieli wyrazić różnice temperatur używając danego stopnia sprężania
i współczynnika Poissona κ.
W tym celu skorzystamy z równania dla gazu idealnego przechodzącego proces adiabatyczny (prawo Poissona) pVκ = C = konst…, gdzie C jest stałą. Teraz obliczymy ciśnienie z równania stanu gazu idealnego
\, które podstawimy do prawa Poissona. Teraz przenosimy stałe (C i K) na jedną stronę
Teraz stosujemy to prawo Poissona dla obu procesów adiabatycznych. Dla adiabatycznego rozszerzania otrzymujemy zależność
\
A dla adiabatycznego ściskania otrzymujemy
\
Teraz odejmujemy drugie równanie od pierwszego i odejmujemy V1κ – 1 z jednej strony i V2κ – 1 z drugiej. Otrzymujemy:
\\
Widzimy, że rzeczywiście udało nam się wyrazić różnice temperatur za pomocą podanych wartości. Teraz podstawiamy tę zależność do wzoru na sprawność i otrzymujemy równanie końcowe:
∗ ∗ ∗ ∗ ∗.