Arbete definieras som den energi man tillför ett föremål genom att utöva en kraft F över en viss sträcka r.

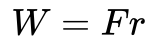
Detta kan t.ex. betyda att man lyfter upp ett föremål en sträcka r mot gravitationen. Den tillförda energin är då potentiell energi. I det här fallet vill jag dock visa hur arbete hänger ihop med rörelseenergi.

Om du applicerar en kraft på ett föremål, för att få det att röra sig snabbare, ökar du dess rörelseenergi.

Jag kommer att visa hur de två hänger ihop med hjälp av en av de rörelseekvationer som jag har behandlat tidigare.

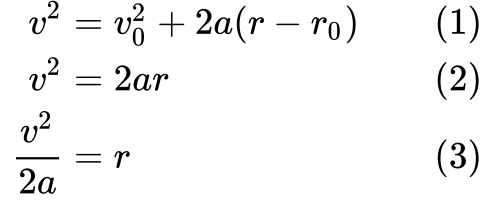
Vi börjar med definitionen (1) och sedan förenklar vi (2) den genom att säga att den initiala hastigheten v₀ och det initiala avståndet r₀ båda är noll.

Slutligt ordnar vi om (3) ekvationen för att få ett sätt att uttrycka r, så att vi kan sätta in det i W = Fr.

Vi vill också bli av med accelerationen från ekvationen, eftersom uttrycket för kinetisk energi inte innehåller den. Låt oss ordna om Newtons andra lag:

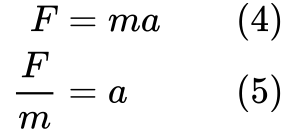
Nu har vi bitarna för att härleda ekvationen för kinetisk energi.

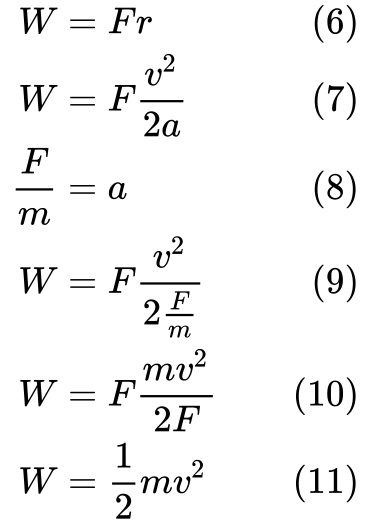
(7) Substituera r med ekvation (3). Sedan kan vi vi ersätta a i ekvation (9) med definition för acceleration i ekvation (8).

Slutligt (11) kan vi se att arbete är lika med kinetisk energi.

När jag av en slump läste igenom det här inlägget igen märkte jag att mitt tillvägagångssätt kunde ha varit mycket enklare.

Om vi börjar med W = Fv²/2a och F = ma så ersätter vi F direkt i stället för a, och får W = mav²/2a istället. Då är a lätt att eliminera och vi får W = mv²/2.