Arbejde defineres som den energi, man tilføjer en genstand ved at påføre en kraft F over en vis afstand r.

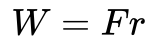
Det kan f.eks. være at løfte en genstand op over en afstand r mod tyngdekraften. Den tilførte energi er i så fald potentiel energi. Men i dette tilfælde vil jeg vise, hvordan arbejde hænger sammen med kinetisk energi.

Hvis man anvender en kraft på en genstand, for at få den til at bevæge sig hurtigere, øger man dens kinetiske energi.

Jeg vil vise, hvordan de to hænger sammen ved hjælp af en af de bevægelsesligninger, som jeg har gennemgået tidligere.

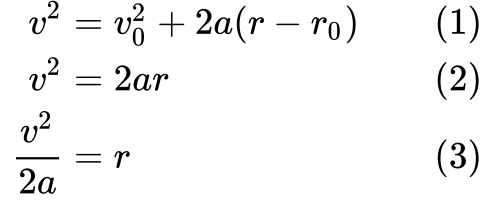
Vi starter med definitionen (1), og så forenkler vi (2) den ved at sige, at initialhastighed v₀ og initial tilbagelagt afstand r₀ begge er nul.

Sidst omarrangerer vi (3) ligningen for at få en måde at udtrykke r på, så vi kan indsætte den i W = Fr.

Vi vil også gerne slippe af med accelerationen fra ligningen, fordi udtrykket for kinetisk energi ikke indeholder den. Lad os omformulere Newtons anden lov:

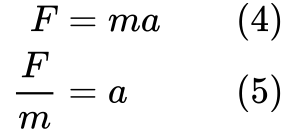
Nu har vi brikkerne til at udlede ligningen for kinetisk energi.

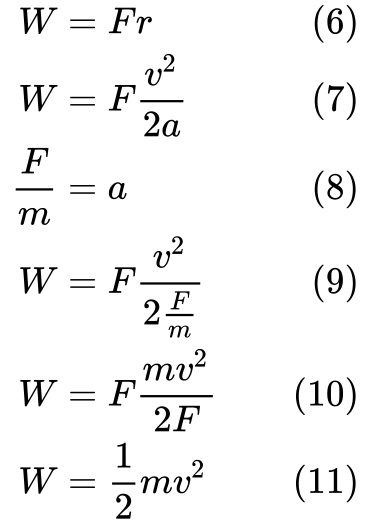
(7) Substituere r med ligning (3). Derefter kan vi vi vi substituere a i ligning (9) med definition for acceleration i ligning (8).

Slutteligt (11) kan vi se, at arbejde er lig med kinetisk energi.

Når jeg tilfældigvis læste dette indlæg igennem igen, bemærkede jeg, at min fremgangsmåde kunne have været meget enklere.

Hvis vi starter med W = Fv²/2a og F = ma, så substituerer vi F direkte i stedet for a, og får W = mav²/2a i stedet. Så er a let at fjerne, og vi ender med W = mv²/2.