Werk is gedefinieerd als de energie, die je aan een voorwerp toevoegt door F een kracht uit te oefenen over een bepaalde afstand r.

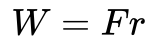
Dit kan bijvoorbeeld betekenen dat je een voorwerp r tegen de zwaartekracht in een afstand omhoog tilt. De toegevoegde energie is dan potentiële energie. In dit geval wil ik echter laten zien hoe arbeid zich verhoudt tot kinetische energie.

Als je een kracht uitoefent op een voorwerp, om het sneller te laten bewegen, verhoog je de kinetische energie ervan.

Ik zal laten zien hoe die twee zich tot elkaar verhouden aan de hand van een van de bewegingsvergelijkingen die ik eerder heb behandeld.

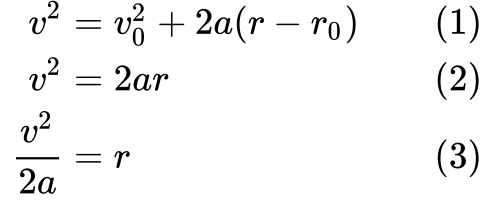
We beginnen met de definitie (1) en dan vereenvoudigen we (2) door te zeggen dat de beginsnelheid v₀ en de aanvankelijk afgelegde afstand r₀ beide nul zijn.

Ten slotte herschikken we (3) de vergelijking om r uit te drukken, zodat we die kunnen substitueren in W = Fr.

We willen ook de versnelling uit de vergelijking halen, omdat de uitdrukking voor kinetische energie die niet bevat. Laten we Newtons tweede wet herschikken:

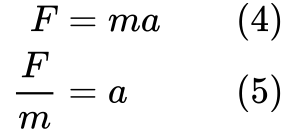
Nu hebben we de stukken om de vergelijking voor kinetische energie af te leiden.

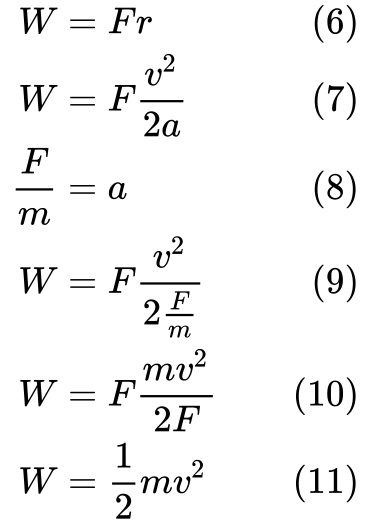
(7) Vervangen r door vergelijking (3). Dan kunnen we a in vergelijking (9) vervangen door definitie voor versnelling in vergelijking (8).

Tot slot (11) kunnen we zien dat arbeid gelijk is aan kinetische energie.

Toen ik deze post toevallig nog eens doorlas viel me op dat mijn aanpak een stuk eenvoudiger had gekund.

Als we beginnen met W = Fv²/2a en F = ma dan substitueren we F direct in plaats van a, en krijgen we W = mav²/2a in plaats daarvan. Dan is a eenvoudig te elimineren en krijgen we W = mv²/2.