Christian Bohr i koncepcja wiązania kooperacyjnegoEdit

W 1904 roku Christian Bohr badał wiązanie hemoglobiny z tlenem w różnych warunkach. Podczas wykreślania nasycenia hemoglobiny tlenem jako funkcji ciśnienia parcjalnego tlenu, otrzymał krzywą sigmoidalną (lub “S-kształtną”). Wskazuje to, że im więcej tlenu jest związane z hemoglobiną, tym łatwiej jest związać więcej tlenu – aż do nasycenia wszystkich miejsc wiążących. Ponadto Bohr zauważył, że rosnące ciśnienie CO2 przesuwa tę krzywą w prawo – tzn. wyższe stężenie CO2 utrudnia hemoglobinie wiązanie tlenu. To ostatnie zjawisko, wraz z obserwacją, że powinowactwo hemoglobiny do tlenu wzrasta wraz ze wzrostem pH, znane jest jako efekt Bohra.

Oryginalna rycina Christiana Bohra, pokazująca sigmoidalny wzrost oksyhemoglobiny w funkcji ciśnienia parcjalnego tlenu.

Mówi się, że cząsteczka receptora wykazuje kooperatywne wiązanie, jeśli jej wiązanie do liganda skaluje się nieliniowo ze stężeniem liganda. Kooperatywność może być pozytywna (jeśli wiązanie cząsteczki liganda zwiększa pozorne powinowactwo receptora, a tym samym zwiększa szansę na wiązanie innej cząsteczki liganda) lub negatywna (jeśli wiązanie cząsteczki liganda zmniejsza powinowactwo, a tym samym zmniejsza prawdopodobieństwo wiązania innych cząsteczek liganda). Ułamkowa zajętość” Y Ż {{displaystyle {{bary}}}

receptora z danym ligandem definiuje się jako ilość miejsc wiążących ligand podzieloną przez całkowitą ilość miejsc wiążących ligand: Y ¯ = + = {displaystyle {{bar {Y}}={{frac {}{+}}={{frac {}{}}}

Jeśli Y Ż = 0 {displaystyle {{bar {Y}}=0}

, to białko jest całkowicie niezwiązane, a jeśli Y Ż = 1 {displaystyle {bar {Y}}=1}

, to jest ono całkowicie nasycone. Jeśli wykres Y Ż {{displaystyle {{bar {Y}}}

w stanie równowagi w funkcji stężenia liganda ma kształt sigmoidalny, tak jak to zaobserwował Bohr dla hemoglobiny, wskazuje to na pozytywną kooperatywność. Jeśli nie jest, nie można powiedzieć o spółdzielczości z patrząc na ten wykres sam.

Pojęcie kooperatywnego wiązania dotyczy tylko cząsteczek lub kompleksów z więcej niż jednym miejscem wiążącym ligand. Jeśli istnieje kilka miejsc wiążących ligand, ale wiązanie ligandu do któregokolwiek z nich nie wpływa na pozostałe, receptor jest określany jako niekooperatywny. Kooperatywność może być homotropowa, gdy ligand wpływa na wiązanie ligandów tego samego rodzaju, lub heterotropowa, gdy wpływa na wiązanie ligandów innego rodzaju. W przypadku hemoglobiny, Bohr zaobserwował homotropową pozytywną kooperatywność (wiązanie tlenu ułatwia wiązanie większej ilości tlenu) i heterotropową negatywną kooperatywność (wiązanie CO2 zmniejsza zdolność hemoglobiny do wiązania tlenu.)

W ciągu XX wieku opracowano różne ramy opisujące wiązanie ligandu z białkiem posiadającym więcej niż jedno miejsce wiążące i obserwowane w tym kontekście efekty kooperacji.

Równanie HillaEdit

Pierwszy opis kooperatywnego wiązania z białkiem wielomiejscowym został opracowany przez A.V. Hilla. Opierając się na obserwacjach wiązania tlenu do hemoglobiny i pomyśle, że kooperatywność wynika z agregacji cząsteczek hemoglobiny, z których każda wiąże jedną cząsteczkę tlenu, Hill zaproponował równanie fenomenologiczne, które od tego czasu zostało nazwane jego imieniem:

Wykres równania Hilla w kolorze czerwonym, pokazujący nachylenie krzywej będące współczynnikiem Hilla oraz punkt przecięcia z osią x podający pozorną stałą dysocjacji. Zielona linia pokazuje krzywą braku współpracy.

Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {displaystyle {}}={{frac {K^{n}}{1+K^{n}}}={{frac {^{n}}{K^{*}+^{n}}}={{{frac {^{n}}{K_{d}^{n}+^{n}}}}

gdzie n {{displaystyle n}

jest “współczynnikiem Hilla”, {displaystyle }

oznacza stężenie liganda, K {displaystyle K}

oznacza pozorną stałą asocjacji (używaną w oryginalnej formie równania), K ∗ {displaystyle K^{*}}

jest empiryczną stałą dysocjacji, a K d {{displaystyle K_{d}}

jest mikroskopową stałą dysocjacji (używaną we współczesnych formach równania i równoważną E C 50 {{displaystyle \mathrm {EC} _{50}}

). Jeśli n < 1 {{displaystyle n<1}

, to układ wykazuje kooperatywność ujemną, natomiast kooperatywność jest dodatnia, jeśli n > 1 {displaystyle n>1}

. Całkowita liczba miejsc wiążących ligand jest górną granicą dla n {displaystyle n}

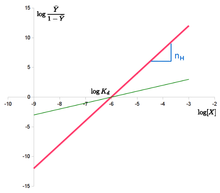
. Równanie Hilla można zlinearyzować jako: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {{displaystyle ἀlog {{frac {{bary}}}{1-{{bary {}}}}=n {}log-n {}log K_{d}}

“Hill plot” uzyskuje się przez wykreślenie log Y ¯ 1 – Y ¯ {{displaystyle {frac {{bar {Y}}}{1-{bar {Y}}}}}

versus log {{displaystyle ™log}

. W przypadku równania Hilla jest to linia o nachyleniu n H {{displaystyle n_{H}}

i przechwycie log ( K d ) {displaystyle \log(K_{d}})}

. Oznacza to, że kooperatywność jest przyjęta jako stała, tzn. nie zmienia się wraz z nasyceniem. Oznacza to również, że miejsca wiążące zawsze wykazują takie samo powinowactwo, a kooperatywność nie wynika z powinowactwa rosnącego ze stężeniem liganda.

Równanie Adair’aEdit

G.S. Adair odkrył, że wykres Hilla dla hemoglobiny nie jest linią prostą i wysunął hipotezę, że powinowactwo wiążące nie jest pojęciem stałym, ale zależy od nasycenia ligandu. Wykazawszy, że hemoglobina zawiera cztery hemy (a więc miejsca wiążące tlen), Adair wyszedł z założenia, że w pełni nasycona hemoglobina powstaje etapami, z formami pośrednimi zawierającymi jedną, dwie lub trzy związane cząsteczki tlenu. Tworzenie się każdego etapu pośredniego z niezwiązanej hemoglobiny można opisać za pomocą pozornej makroskopowej stałej asocjacji K i {\i1}.

. Uzyskane w ten sposób ułamkowe obłożenie można wyrazić jako: Y ¯ = 1 4 ⋅ K I + 2 K I I 2 + 3 K I I I 3 + 4 K I V 4 1 + K I + K I I 2 + K I I 3 + K I V 4 {fracplaystyle } {Y}}={{frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, dla dowolnego białka z n miejscami wiążącymi ligand:

Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {{displaystyle}}={{frac {1}{n}}}{{frac {K_{I}+2K_{II}^{2}+ldoty +nK_{n}^{n}}}{1+K_{I}+K_{II}^{2}+ldoty +K_{n}^{n}}}}

gdzie n oznacza liczbę miejsc wiążących, a każde K i {{displaystyle K_{i}}

jest zespoloną stałą asocjacji, opisującą wiązanie i cząsteczek ligandu.Łącząc metodę Adair’a z wykresem Hill’a otrzymujemy współczesną eksperymentalną definicję kooperatywności (Hill, 1985, Abeliovich, 2005). Wynikowy współczynnik Hilla, lub bardziej poprawnie, nachylenie wykresu Hilla obliczone na podstawie równania Adair’a, może być pokazane jako stosunek wariancji liczby wiązań do wariancji liczby wiązań w równoważnym systemie nie oddziałujących miejsc wiążących. Tak więc współczynnik Hilla definiuje kooperatywność jako statystyczną zależność jednego miejsca wiążącego od stanu innego miejsca (miejsc).

Równanie KlotzaEdit

Pracując nad białkami wiążącymi wapń, Irving Klotz zdekonwoluował stałe asocjacyjne Adair’a poprzez uwzględnienie stopniowego tworzenia etapów pośrednich i próbował wyrazić kooperatywne wiązanie w kategoriach procesów elementarnych rządzonych prawem działania masy. W jego ramach, K 1 {{1}}

jest stałą asocjacji regulującą wiązanie pierwszej cząsteczki liganda, K 2 {displaystyle K_{2}}

stała asocjacji rządząca wiązaniem drugiej cząsteczki liganda (gdy pierwsza jest już związana) itd. Dla Y Ż {{displaystyle {{bar {Y}}

, daje to: Y Ż = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {{displaystyle {}}={ {{frac {1}{n}}}{{frac {K_{1}+2K_{1}K_{2}^{2}+}ldots +n}left(K_{1}K_{2}}}ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Warto zauważyć, że stałe K 1 {{displaystyle K_{1}}

, K 2 {displaystyle K_{2}}

i tak dalej nie odnoszą się do poszczególnych miejsc wiążących. Opisują one ile miejsc wiążących jest zajętych, a nie które z nich. Ta forma ma tę zaletę, że kooperatywność jest łatwo rozpoznawalna przy rozpatrywaniu stałych asocjacji. Jeśli wszystkie miejsca wiążące ligand są identyczne z mikroskopową stałą asocjacji K {{displaystyle K}

, można by oczekiwać K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K { {displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}

(czyli K i = n – i + 1 i K {{displaystyle K_{i}={{frac {n-i+1}{i}}K}

) przy braku kooperatywności. Z dodatnią kooperatywnością mamy do czynienia, jeśli K i {{i}}

leży powyżej tych oczekiwanych wartości dla i > 1 { {displaystyle i>1}

.

Równanie Klotza (które czasami jest również nazywane równaniem Adair-Klotza) jest nadal często używane w literaturze eksperymentalnej do opisywania pomiarów wiązania ligandów w kategoriach sekwencyjnych pozornych stałych wiązania.

Równanie PaulingaEdit

W połowie XX wieku wzrosło zainteresowanie modelami, które nie tylko fenomenologicznie opisywałyby krzywe wiązania, ale oferowałyby leżący u ich podstaw mechanizm biochemiczny. Linus Pauling ponownie zinterpretował równanie przedstawione przez Adair’a, zakładając, że jego stałe są kombinacją stałej wiązania dla liganda ( K {displaystyle K}

w równaniu poniżej) i energii pochodzącej z interakcji pomiędzy podjednostkami współpracującego białka ( α {displaystyle \alpha }

poniżej). Pauling w rzeczywistości wyprowadził kilka równań, w zależności od stopnia interakcji między podjednostkami. Opierając się na błędnych założeniach dotyczących lokalizacji hemów, wybrał niewłaściwe równanie do opisu wiązania tlenu przez hemoglobinę, zakładając, że podjednostki są ułożone w kwadrat. Poniższe równanie podaje równanie dla struktury tetraedrycznej, które byłoby bardziej dokładne w przypadku hemoglobiny: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 + α 6 K 4 4 {} = {{frac {K+3}}} {}K^{2}^{2}+3}alfa {}^{3}K^{3}^{3}+alfa {}^{6}K^{4}^{4}}{1+4K+6}alfa {}K^{2}^{2}+4}alfa {}^{3}K^{3}^{3}+alfa {}^{6}K^{4}^{4}}}}}

Model KNFEdit

Oparty na wynikach pokazujących, że struktura białek kooperacyjnych zmieniała się po związaniu z ich ligandem, Daniel Koshland i współpracownicy udoskonalili biochemiczne wyjaśnienie mechanizmu opisanego przez Paulinga. Model Koshlanda-Némethy-Filmera (KNF) zakłada, że każda podjednostka może istnieć w jednej z dwóch konformacji: aktywnej lub nieaktywnej. Wiązanie liganda do jednej z podjednostek wywołuje natychmiastową zmianę konformacyjną tej podjednostki z konformacji nieaktywnej do aktywnej, mechanizm ten określany jest jako “indukowane dopasowanie”. Kooperatywność, zgodnie z modelem KNF, wynikałaby z oddziaływań pomiędzy podjednostkami, których siła zmienia się w zależności od względnych konformacji zaangażowanych podjednostek. Dla struktury tetraedrycznej (rozważali również struktury liniowe i kwadratowe) zaproponowali następujący wzór:

Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {{fracracklor}} {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Gdzie K X {{X}}

jest stałą asocjacji dla X, K t {{displaystyle K_{t}}

to stosunek stanów B i A w nieobecności liganda (“przejście”), K A B {{displaystyle K_{AB}}

i K B B {{displaystyle K_{BB}}

są względnymi stabilnościami par sąsiadujących podjednostek w stosunku do pary, w której obie podjednostki są w stanie A (Zauważ, że dokument KNF w rzeczywistości przedstawia N s {displaystyle N_{s}}

, liczbę zajętych miejsc, która jest tutaj 4 razy większa od Y Ż {displaystyle N_{s}}

).

Model MWCEdit

Schemat reakcji modelu Monoda-Wymana-Changeux dla białka zbudowanego z dwóch protomerów. Protomer może istnieć w dwóch stanach, z których każdy ma inne powinowactwo do liganda. L to stosunek stanów przy braku liganda, c to stosunek powinowactw.

Schemat energetyczny modelu Monoda-Wymana-Changeuxa białka złożonego z dwóch protomerów. Większe powinowactwo liganda do stanu R oznacza, że ten ostatni jest preferencyjnie stabilizowany przez wiązanie.

Model Monoda-Wymana-Changeuxa (MWC) dla uzgodnionych przejść allosterycznych poszedł o krok dalej, badając kooperatywność w oparciu o termodynamikę i trójwymiarowe konformacje. Został on pierwotnie sformułowany dla białek oligomerycznych z symetrycznie rozmieszczonymi, identycznymi podjednostkami, z których każda posiada jedno miejsce wiążące ligand. Zgodnie z tym założeniem, dwa (lub więcej) zamienne stany konformacyjne białka allosterycznego współistniej± w równowadze termicznej. Stany te – często określane jako napięty (T) i zrelaksowany (R) – różnią się powinowactwem do cząsteczki liganda. Stosunek pomiędzy tymi dwoma stanami jest regulowany przez wi±zanie cz±steczek ligandu, który stabilizuje stan o wyższym powinowactwie. Co ważne, wszystkie podjednostki cząsteczki zmieniają stany w tym samym czasie, zjawisko znane jako “concerted transition”.

Stała izomeryzacji allosterycznej L opisuje równowagę pomiędzy obydwoma stanami, gdy nie jest związana żadna cząsteczka liganda: L = {{displaystyle L={frac {{left}}}

. Jeśli L jest bardzo duże, to większość białka istnieje w stanie T przy braku liganda. Jeśli L jest małe (bliskie jedności), stan R jest prawie tak samo zaludniony jak stan T. Stosunek stałych dysocjacji liganda ze stanów T i R opisuje stała c: c = K d R K d T {{displaystyle c={{frac {K_{d}^{R}}{K_{d}^{T}}}}

. Jeśli c = 1 {{displaystyle c=1}}

, to oba stany R i T mają takie samo powinowactwo do liganda i ligand nie wpływa na izomeryzację. Wartość c wskazuje również, jak bardzo zmienia się równowaga pomiędzy stanami T i R po związaniu liganda: im mniejsze c, tym bardziej równowaga przesuwa się w kierunku stanu R po jednym związaniu. Z α = K d R {{displaystyle }alpha ={frac {}{K_{d}^{R}}}}

, zajętość frakcyjna jest opisana jako: Y Ż = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {displaystyle {}}={frac {{alfa (1+alfa )^{n-.1}+Lcalfa (1+calfa )^{n-1}}{(1+alfa )^{n}+L(1+calfa )^{n}}}}

Sygmoidalny wykres Hilla białek allosterycznych może być analizowany jako stopniowe przejście ze stanu T (niskie powinowactwo) do stanu R (wysokie powinowactwo) wraz ze wzrostem nasycenia. Nachylenie wykresu Hilla również zależy od nasycenia, z wartością maksymalną w punkcie przegięcia. Punkty przecięcia obu asymptot z osią y pozwalają na określenie powinowactwa obu stanów do liganda.

Wykres Hilla funkcji wiązania MWC w kolorze czerwonym, czystego stanu T i R w kolorze zielonym. Wraz z przesunięciem konformacji z T do R, zmienia się również funkcja wiązania. Punkty przecięcia z osią x podają pozorną stałą dysocjacji, jak również mikroskopowe stałe dysocjacji stanów R i T.

W białkach, zmiana konformacyjna jest często związana z aktywnością, lub aktywnością wobec specyficznych celów. Taka aktywność jest często tym, co jest istotne fizjologicznie lub tym, co jest mierzone eksperymentalnie. Stopień zmiany konformacyjnej jest opisywany przez funkcję stanu R Ż {{displaystyle {{bar {R}}}

, która oznacza frakcję białka obecną w R {displaystyle R}}

state. Jak wynika z diagramu energetycznego, R – {displaystyle {R}}

wzrasta w miarę wiązania kolejnych cząsteczek liganda. Wyrażenie na R – {{displaystyle {{bar {{R}}}

jest: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {{displaystyle {{bar {R}}={frac {(1+alfa )^{n}}}{(1+alfa )^{n}+L(1+c α )^{n}}}}

Kluczowym aspektem modelu MWC jest to, że krzywe dla Y ¯ {{displaystyle {{frac}}}

i R Ż {{displaystyle {{bar {R}}}

nie pokrywają się, czyli nasycenie frakcyjne nie jest bezpośrednim wskaźnikiem stanu konformacyjnego (a więc i aktywności). Co więcej, zakresy kooperatywności wiązania i kooperatywności aktywacji mogą być bardzo różne: skrajnym przypadkiem jest silnik flagi bakterii o współczynniku Hilla 1,7 dla wiązania i 10,3 dla aktywacji. Nadliniowość odpowiedzi jest czasami nazywana ultraczułością.

Jeśli białko allosteryczne wiąże się z celem, który również ma wyższe powinowactwo do stanu R, to wiązanie celu dalej stabilizuje stan R, stąd zwiększenie powinowactwa liganda. Jeśli, z drugiej strony, cel wiąże się preferencyjnie do stanu T, wówczas wiązanie celu będzie miało negatywny wpływ na powinowactwo liganda. Takie cele są nazywane modulatorami allosterycznymi.

Od czasu powstania, ramy MWC zostały rozszerzone i uogólnione. Zaproponowano odmiany, na przykład, aby zaspokoić białka z więcej niż dwoma stanami, białka, które wiążą się z kilkoma typami ligandów lub kilkoma typami modulatorów allosterycznych oraz białka z nieidentycznymi podjednostkami lub miejscami wiązania ligandów.

.