El trabajo se define como la energía, que se añade a un objeto aplicando una fuerza F a lo largo de cierta distancia r.

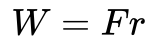
Esto podría significar, por ejemplo, levantar un objeto una distancia r contra la gravedad. La energía añadida es entonces energía potencial. Sin embargo, en este caso quiero mostrar cómo se relaciona el trabajo con la energía cinética.

Si aplicas una fuerza a un objeto, para que se mueva más rápido, aumentas su energía cinética.

Mostraré cómo se relacionan ambas usando una de las ecuaciones de movimiento que he cubierto anteriormente.

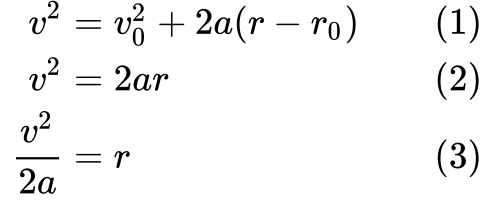
Empezamos con la definición (1) y luego la simplificamos (2) diciendo que la velocidad inicial v₀ y la distancia inicial recorrida r₀ son ambas cero.

Finalmente reordenamos (3) la ecuación para obtener una forma de expresar r, de modo que podamos sustituirla en W = Fr.

También queremos deshacernos de la aceleración de la ecuación, porque la expresión para la energía cinética no la contiene. Reorganicemos la segunda ley de Newton:

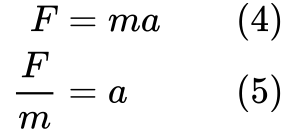
Ahora tenemos las piezas para derivar la ecuación de la energía cinética.

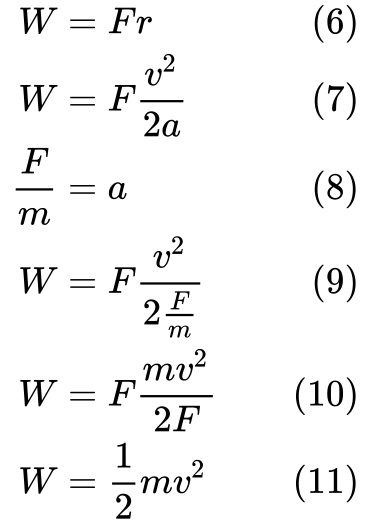
(7) sustituye r por la ecuación (3). Entonces podemos sustituir a en la ecuación (9) con la definición para la aceleración en la ecuación (8).

Finalmente (11) podemos ver que el trabajo es igual a la energía cinética.

Al leer de nuevo este post por casualidad me di cuenta de que mi enfoque podría haber sido mucho más simple.

Si empezamos con W = Fv²/2a y F = ma entonces sustituimos F directamente en lugar de a, y obtenemos W = mav²/2a en su lugar. Entonces a se elimina fácilmente y terminamos con W = mv²/2.