Pracę definiuje się jako energię dodaną do obiektu przez przyłożenie siły F na pewną odległość r.

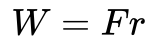
Może to oznaczać np. podniesienie obiektu na odległość r wbrew grawitacji. Dodana energia jest wtedy energią potencjalną. Jednak w tym przypadku chcę pokazać, jak praca wiąże się z energią kinetyczną.

Jeśli przykładasz siłę do obiektu, aby poruszał się szybciej, zwiększasz jego energię kinetyczną.

Pokażę, jak te dwie rzeczy są powiązane, używając jednego z równań ruchu, które omówiłem wcześniej.

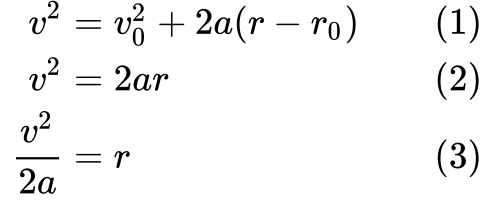
Zaczynamy od definicji (1), a następnie upraszczamy ją (2) mówiąc, że prędkość początkowa v₀ i początkowa przebyta droga r₀ są równe zero.

W końcu przekształcamy (3) równanie, aby uzyskać sposób wyrażenia r, tak abyśmy mogli podstawić je do W = Fr.

Chcemy również pozbyć się przyspieszenia z równania, ponieważ wyrażenie na energię kinetyczną nie zawiera go. Przekształćmy drugie prawo Newtona:

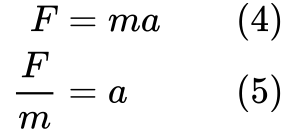
Teraz mamy kawałki do wyprowadzenia równania na energię kinetyczną.

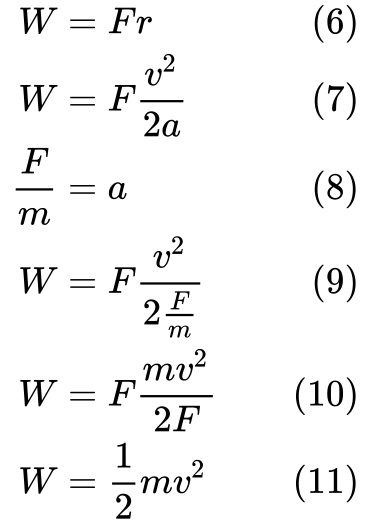
(7) podstawiamy r do równania (3). Następnie możemy zastąpić a w równaniu (9) z definicją przyspieszenia w równaniu (8).

W końcu (11) widzimy, że praca równa się energii kinetycznej.

Przypadkowo czytając ten post ponownie zauważyłem, że moje podejście mogło być o wiele prostsze.

Jeśli zaczniemy od W = Fv²/2a i F = ma to podstawimy F bezpośrednio zamiast a i otrzymamy W = mav²/2a. Wtedy a jest łatwo wyeliminować i kończymy z W = mv²/2.

.